
经典物理学(能量交换是连续的)的解释 (1)维恩公式:根据热力学和电磁理论,维恩给出了如下黑 体辐射能量密度p(y,T)分布公式 p(v,T)dv v3o(v/T)dv 在对黑体的发射和吸收做特殊的假设后 Wilhelm Wien 1864-1928 p(v,T)dv cv3e-c2v/Tdv 1911 Nobel Prize (2)瑞利-金斯公式:根据经典电动力学推导出空腔 单位体积内的辐射频率在v→v+dv之间独立振动的 数目为n=8πv2/c3,由经典统计的能均分定理(每 一个振动的能量是kT,这是能量连续变换的必然结 John Strutt Rayleigh James Jeans 果),从而得到黑体辐射的能量密度分布公式为 1842-1919 1877-1946 p(v,T)dv 8nv2/c3kTdv
经典物理学(能量交换是连续的)的解释 (1)维恩公式:根据热力学和电磁理论,维恩给出了如下黑 体辐射能量密度𝜌 𝜈, 𝑇 分布公式 𝜌 𝜈, 𝑇 𝑑𝜈 = 𝜈 3𝜑 𝜈/𝑇 𝑑𝜈 在对黑体的发射和吸收做特殊的假设后 𝜌 𝜈, 𝑇 𝑑𝜈 = 𝑐1𝜈 3𝑒 −𝑐2𝜈/𝑇𝑑𝜈 (2)瑞利-金斯公式:根据经典电动力学推导出空腔 单位体积内的辐射频率在𝜈 ⟶ 𝜈 + 𝑑𝜈之间独立振动的 数目为𝑛 = 8𝜋𝜈 2 /𝑐 3,由经典统计的能均分定理(每 一个振动的能量是𝑘𝑇,这是能量连续变换的必然结 果),从而得到黑体辐射的能量密度分布公式为 𝜌 𝜈, 𝑇 𝑑𝜈 = 8𝜋𝜈 2 /𝑐 3𝑘𝑇𝑑𝜈 Wilhelm Wien 1864-1928 1911 Nobel Prize John Strutt Rayleigh 1842-1919 James Jeans 1877-1946
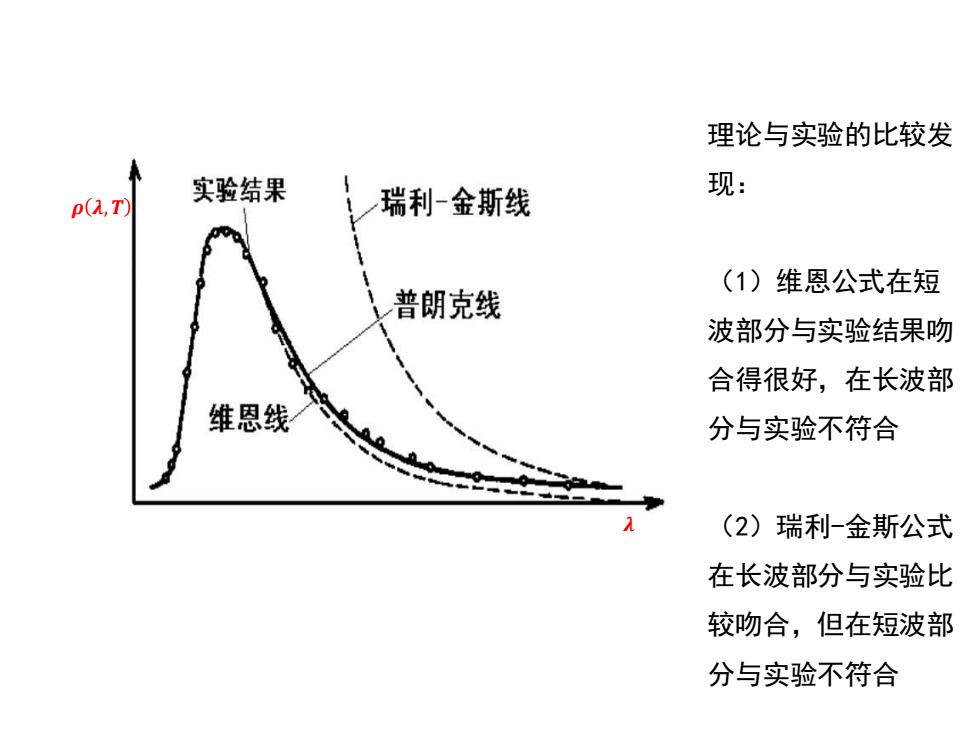
理论与实验的比较发 实验结果 瑞利一金斯线 现: p(A,T) (1)维恩公式在短 普朗克线 波部分与实验结果吻 合得很好,在长波部 维恩线 分与实验不符合 (2)瑞利-金斯公式 在长波部分与实验比 较吻合,但在短波部 分与实验不符合
𝝆 𝝀 , 𝑻 𝝀 理论与实验的比较发 现:(1)维恩公式在短 波部分与实验结果吻 合得很好,在长波部 分与实验不符合 (2)瑞利-金斯公式 在长波部分与实验比 较吻合,但在短波部 分与实验不符合

为了克服以上困难,1900年,普朗克提出了“能量子”假说: (1)物质与电磁场间的能量交换以所谓的“能包”的形式一 份一份的进行,每份的大小为,称为一个能量子。在这种量 子化的交换方式下,不论物质还是电磁场,其能量变化都不是 连续的。 Max Karl Ernst Ludwig Planck (2)或者说,物体吸收或发射频率为v的电磁波,只能以“量8i18s8-4 October 1947 1918 Nobel Prize 子”方式进行,每个“量子”的能量e=hv 在这个假说下,根据经典电磁理论和玻尔兹曼分布,普朗克给出了黑体辐射 的能量密度分布 P(v,T)dv= 8πhv3 1 c3 ehv/KT-1dv h=6.626×10-34·s=6.626×10-34kg·m2.s-1,具有作用量的量纲
在这个假说下,根据经典电磁理论和玻尔兹曼分布,普朗克给出了黑体辐射 的能量密度分布 𝜌 𝜈, 𝑇 𝑑𝜈 = 8𝜋ℎ𝜈 3 𝑐 3 𝟏 𝒆 𝒉𝝂/𝒌𝑻 − 𝟏 𝑑𝜈 为了克服以上困难,1900年,普朗克提出了“能量子”假说: (1)物质与电磁场间的能量交换以所谓的“能包”的形式一 份一份的进行,每份的大小为𝜀,称为一个能量子。在这种量 子化的交换方式下,不论物质还是电磁场,其能量变化都不是 连续的。 (2)或者说,物体吸收或发射频率为𝜈的电磁波,只能以“量 子”方式进行,每个“量子”的能量𝜀 = ℎ𝜈 Max Karl Ernst Ludwig Planck 23 April 1858--4 October 1947 1918 Nobel Prize 𝒉 = 𝟔. 𝟔𝟐𝟔 × 𝟏𝟎−𝟑𝟒𝐉 ∙ 𝐬 = 𝟔. 𝟔𝟐𝟔 × 𝟏𝟎−𝟑𝟒𝐤𝐠 ∙ 𝐦𝟐 ∙ 𝐬 −𝟏 ,具有作用量的量纲
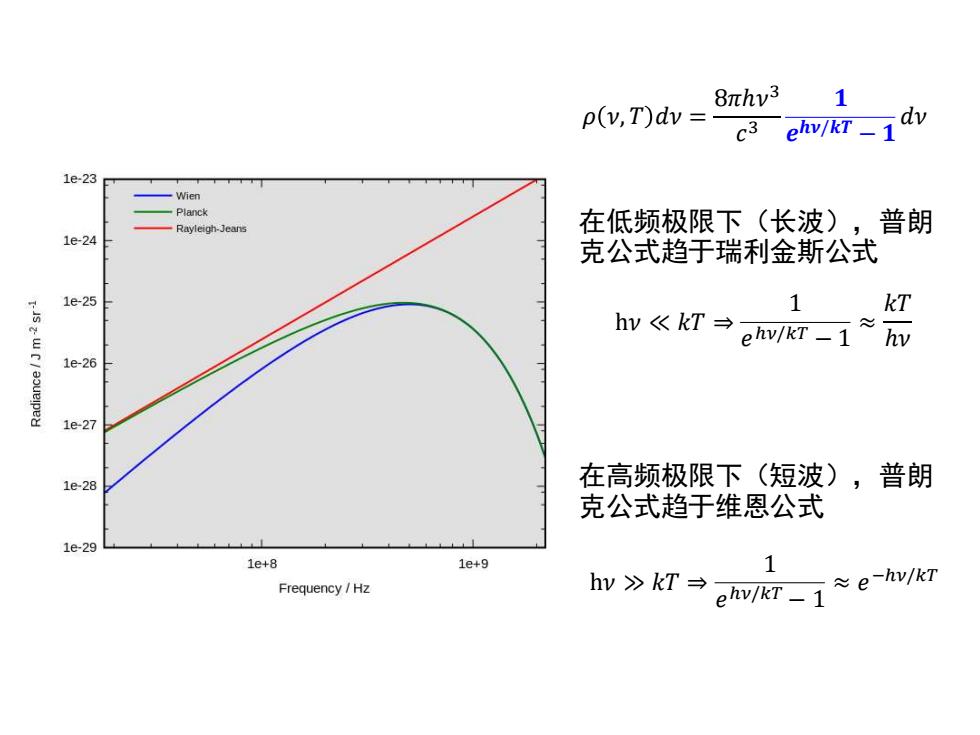
8nhv3 1 p(v,T)dv = c3 ehv/KT_1 dv 1e-23 Wien -Planck -Rayleigh-Jeans 在低频极限下(长波),普朗 1e-24 克公式趋于瑞利金斯公式 1e25 1 kT 日 hv《kT→hv/kT-1hw 1e-26 1e27 1e-28 在高频极限下(短波),普朗 克公式趋于维恩公式 1e29 1e+8 1e+9 1 Frequency /Hz hv>kT ev/kT-1≈e-h/kT
在低频极限下(长波),普朗 克公式趋于瑞利金斯公式 h𝜈 ≪ 𝑘𝑇 ⇒ 1 𝑒 ℎ𝜈/𝑘𝑇 − 1 ≈ 𝑘𝑇 ℎ𝜈 在高频极限下(短波),普朗 克公式趋于维恩公式 h𝜈 ≫ 𝑘𝑇 ⇒ 1 𝑒 ℎ𝜈/𝑘𝑇 − 1 ≈ 𝑒 −ℎ𝜈/𝑘𝑇 𝜌 𝜈, 𝑇 𝑑𝜈 = 8𝜋ℎ𝜈 3 𝑐 3 𝟏 𝒆 𝒉𝝂/𝒌𝑻 − 𝟏 𝑑𝜈

The Planck's constant h is a fundamental constant,playing a fundamental role in the quantum theory (when divided by 2,it is referred to as h-bar) ·h=6.62606957×10-34m2kg/s0s .(When multiplied by the frequency)it defines the 'quantum of energy'(the minimum quantity of energy which can be exchanged) Represents the connection between the wavelength and momentum of particles(wave-particle duality!) It defines the scale at which the natural phenomena become "quantistic"(and classical behavior disappears) “我今天推导出了一个概念,我想它应该和牛顿的那些成果一样伟大,并富于革命性
“我今天推导出了一个概念,我想它应该和牛顿的那些成果一样伟大,并富于革命性