二、红外光谱的基本原理 双原子分子的谐振子模型 ·双原子分子中两个原子(质量分别为m1,m2)之间的振动,可以简 化成质量为μ的单个质点的运动 4=%m2 m1+m, 1 m2 ●wO 伸 ·该质点相对于其平衡位置的位移q等于核间距的变化 ·可以把这个质点近似看作是一个谐振子,其动能T和势能V分别为 T-3ug 2 V=-kg? 式中,k是振动力常数
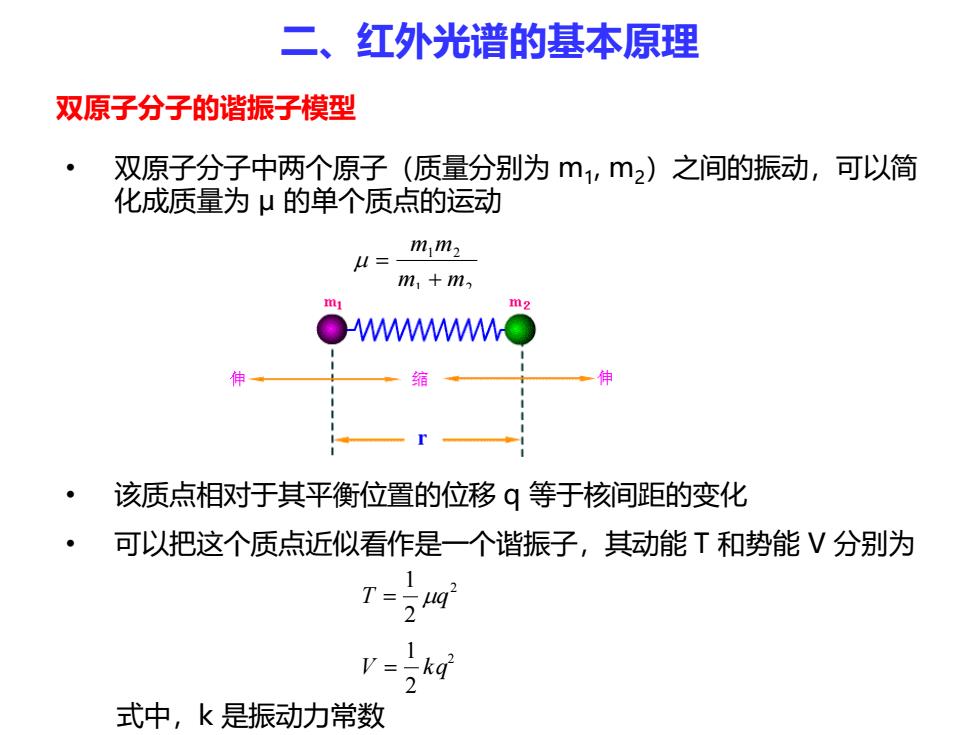
• 双原子分子中两个原子(质量分别为 m1 , m2)之间的振动,可以简 化成质量为 μ 的单个质点的运动 • 该质点相对于其平衡位置的位移 q 等于核间距的变化 • 可以把这个质点近似看作是一个谐振子,其动能 T 和势能 V 分别为 双原子分子的谐振子模型 2 2 1 T q 2 2 1 V k q 式中,k 是振动力常数 1 2 1 2 m m m m 二、红外光谱的基本原理

二、红外光谱的基本原理 双原子分子的谐振子模型 ·根据量子力学,谐振子的总能量是量子化的 谐振子的能量: E张=hvn+3 式中,E振-谐振子能量,单位10-7J n-振动量子数(n=0,1,2,3,.) h-普朗克常数 V-谐振子的振动频率,单位:s1 =1 2πY4 ·因此,谐振子的总能量: h k E振 (n+-) 2πV4
• 根据量子力学,谐振子的总能量是量子化的 • 谐振子的能量: 式中,E振 – 谐振子能量,单位 10-7 J n – 振动量子数 (n = 0, 1, 2, 3, .) h – 普朗克常数 ν – 谐振子的振动频率,单位:s -1 ) 2 1 E振 h (n k 2 1 • 因此,谐振子的总能量: ) 2 1 ( 2 n h k E 振 双原子分子的谐振子模型 二、红外光谱的基本原理

二、红外光谱的基本原理 双原子分子的谐振子模型 ·谐振子的总能量: -(n+-) ,因此,振动能级从n=0向n=1能级跃迁时的能量变化为: h k △E振=1 2πV4 。 激发振动能级从n=0向n=1能级跃迁所需吸收的能量为: AE银=hy= hc=hco 1 波数。= 式中, c-光速; h-普朗克常数 V-光频率; 入-光的波长 σ-波数
• 因此,振动能级从 n = 0 向 n = 1 能级跃迁时的能量变化为: h k E 2 振 式中, c – 光速; h – 普朗克常数 ν – 光频率; λ – 光的波长 σ – 波数 • 激发振动能级从 n = 0 向 n = 1 能级跃迁所需吸收的能量为: • 谐振子的总能量: ) 2 1 ( 2 n h k E 振 1 波数 振 hc hc E h 双原子分子的谐振子模型 二、红外光谱的基本原理

二、红外光谱的基本原理 双原子分子的谐振子模型 当c以cm/s为单位,入以cm为单位时,即得到谐振子的基频振动 吸收波数o(cm-1): 1 k 0= 2π·cV4 式中,c-光速 μ-谐振子质量 k一振动力常数 ● 双原子分子的振动力常数k只与电子云密度和核电荷有关,与质量 无关 同种元素,k值相同
式中,c – 光速 μ – 谐振子质量 k – 振动力常数 • 当 c 以cm/s为单位,λ 以 cm 为单位时,即得到谐振子的基频振动 吸收波数 σ (cm-1): k c 2 1 • 双原子分子的振动力常数 k 只与电子云密度和核电荷有关,与质量 无关 同种元素,k 值相同 双原子分子的谐振子模型 二、红外光谱的基本原理

二、红外光谱的基本原理 双原子分子的谐振子模型 谐振子选择定则: 在振动过程中偶极矩不发生变化的振动,如果△=0,不产生振动 光谱 在振动过程中偶极矩发生变化的振动,凡是符合△=±1的跃迁都 是允许的 因为n=0,1,2,3,.,谐振子可以发生0→1,1→2,2→ 3,.跃迁 但是,按照麦克斯韦-波尔兹曼分布定律,绝大多数的振动能级跃迁 都是从电子基态中的n=0向n=1能级跃迁 如果振动能级由n=0向n=1跃迁,即当振动量子数由n=0变到n= 1时,分子所吸收的波数等于谐振子的振动频率,这种振动叫做基频振动
谐振子选择定则: • 在振动过程中偶极矩不发生变化的振动,如果∆n = 0,不产生振动 光谱 • 在振动过程中偶极矩发生变化的振动,凡是符合∆n = ± 1的跃迁都 是允许的 因为n = 0, 1, 2, 3, .,谐振子可以发生 0 → 1,1 → 2,2 → 3,. 跃迁 但是,按照麦克斯韦-波尔兹曼分布定律,绝大多数的振动能级跃迁 都是从电子基态中的 n = 0 向 n = 1 能级跃迁 双原子分子的谐振子模型 二、红外光谱的基本原理 • 如果振动能级由 n = 0 向 n = 1 跃迁,即当振动量子数由 n = 0 变到 n = 1 时,分子所吸收的波数等于谐振子的振动频率,这种振动叫做基频振动