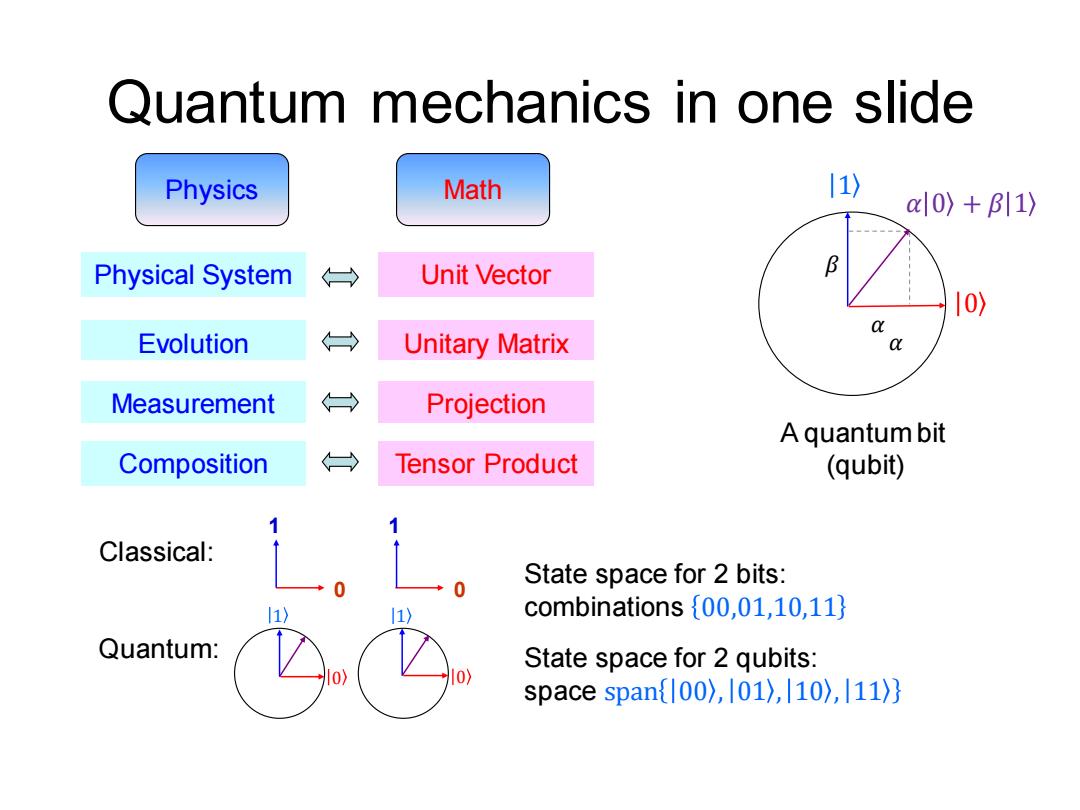
Quantum mechanics in one slide Physics Math 11) a0)+B11〉 Physical System Unit Vector 10) Evolution Unitary Matrix Measurement → Projection A quantum bit Composition → Tensor Product (qubit) Classical: State space for 2 bits: 11) 11) combinations {00,01,10,11} Quantum: State space for 2 qubits: 0) space span{00),101),|10),|11)}
Quantum mechanics in one slide Physics Math Composition Tensor Product Measurement Projection Evolution Unitary Matrix Physical System Unit Vector 1 0 1 0 Classical: Quantum: State space for 2 bits: combinations 00,01,10,11 State space for 2 qubits: space span 00 , 01 , 10 , 11 A quantum bit (qubit) 𝛼 0 + 𝛽 1 0 1 𝛽 𝛼 𝛼 1 1 0 0

Density matrix If a system is in state with probability pi and in stateψ2〉with probability p2,then the system is in a mixed state. The mixed state is represented as a density matrix p=p1lψ1)1|+p2lψ2)Kψ2l. ·In general,,if a system is in stateψi〉with probability pi,then the mixed state is p=∑ipilwi)ψil ·For pure state),p=lψ)Kψ
Density matrix • If a system is in state 𝜓1 with probability 𝑝1, and in state 𝜓2 with probability 𝑝2, then the system is in a mixed state. • The mixed state is represented as a density matrix 𝜌 = 𝑝1 𝜓1 𝜓1 + 𝑝2 𝜓2 𝜓2 . • In general, if a system is in state 𝜓𝑖 with probability 𝑝𝑖 , then the mixed state is 𝜌 = σ𝑖 𝑝𝑖 𝜓𝑖 𝜓𝑖 • For pure state 𝜓 , 𝜌 = 𝜓 𝜓

Density matrix Fact.A matrix p is a density matrix of some mixed quantum state iff p is positive semi-definite (psd) -Tr(p)=1. 。Recall: -A matrix M is psd if all its eigenvalues are nonnegative.Equivalently,if (vMv)>0,Vv. -The trace of a matri>ⅸM is Tr(M)=∑iMii:
Density matrix • Fact. A matrix 𝜌 is a density matrix of some mixed quantum state iff – 𝜌 is positive semi-definite (psd) – Tr 𝜌 = 1. • Recall: – A matrix 𝑀 is psd if all its eigenvalues are nonnegative. Equivalently, if 𝑣 𝑀 𝑣 ≥ 0, ∀𝑣. – The trace of a matrix 𝑀 is Tr 𝑀 = σ𝑖 𝑀𝑖𝑖

Postulates on mixed states Unitary operation U:pUpUt For pure state p=)(,it becomes UpUt Ulφ)KφlUf=lp')Kφ'|whereφ〉=Ulφ). Orthogonal measurement {),...va):outcome i occurs with probabilityp)2,and the system collapses to p'=i)(il. For pure statep =(l,the probability is)2, and the collapsed state is ) If we measure p E Caxd in the computational basis 1),2),...,d),then Pr[outcome i occurs]pii, the i-th diagonal entry of p
Postulates on mixed states • Unitary operation 𝑈: 𝜌 ↦ 𝑈𝜌𝑈 † – For pure state 𝜌 = 𝜙 𝜙 , it becomes 𝑈𝜌𝑈 † = 𝑈 𝜙 𝜙 𝑈 † = 𝜙 ′ 𝜙 ′ where 𝜙 ′ = 𝑈 𝜙 . • Orthogonal measurement 𝜓1 , … 𝜓𝑑 : outcome 𝑖 occurs with probability 𝜓 𝜌 𝜓 2 , and the system collapses to 𝜌 ′ = 𝜓𝑖 𝜓𝑖 . – For pure state 𝜌 = 𝜙 𝜙 , the probability is 𝜙|𝜓𝑖 2 , and the collapsed state is 𝜓𝑖 . • If we measure 𝜌 ∈ ℂ 𝑑×𝑑 in the computational basis 1 , 2 , … , 𝑑 , then Pr outcome 𝑖 occurs = 𝜌𝑖𝑖, the 𝑖-th diagonal entry of 𝜌

·Composition of p1andp2 is just p1☒p2 -For pure state p=and P2= lφ2)Kφ2l,the jo'int state is |Φ1Kφ1l☒|φ2Xφ2 =(φ1〉⑧1φ2)((φ1l☒(φ2) Recall tensor product of matrices: a11b11a11b12 a12b11 a12b12 a11b21a11b22 a12b21 a12b22 a21b11 a21b12 a22b11 a22b12 La21b21 a21b22 a22b21 a22b22」
• Composition of 𝜌1 and 𝜌2 is just 𝜌1 ⊗ 𝜌2 – For pure state 𝜌1 = 𝜙1 𝜙1 and 𝜌2 = 𝜙2 𝜙2 , the joint state is 𝜙1 𝜙1 ⊗ 𝜙2 𝜙2 = 𝜙1 ⊗ 𝜙2 𝜙1 ⊗ 𝜙2 • Recall tensor product of matrices: 𝑎11 𝑎12 𝑎21 𝑎22 ⊗ 𝑏11 𝑏12 𝑏21 𝑏22 = 𝑎11𝑏11 𝑎11𝑏12 𝑎11𝑏21 𝑎11𝑏22 𝑎12𝑏11 𝑎12𝑏12 𝑎12𝑏21 𝑎12𝑏22 𝑎21𝑏11 𝑎21𝑏12 𝑎21𝑏21 𝑎21𝑏22 𝑎22𝑏11 𝑎22𝑏12 𝑎22𝑏21 𝑎22𝑏22