
。线偏振光的解析表示 () >x 6=0 6=π 在观测时间内,日不变。 E0=Ec0s0r 了 Ex(t)=Ax cos ot E(t)=Ay cos(Ot+δ〉 若δ=0,线偏振于位于一、三象限;若δ=士π,线偏 振于二、四象限

。传播方向相同、振动方向互相垂直、相位差恒定的线 偏振光的叠加可以合成圆偏振光和椭圆偏振光。 振动面内光矢量的端,点轨迹分别为圆和椭圆

Ex =Ax cos(ot-kz) E,=Aycos(t-kz+δ) 主 A 原P+经P-2经原)co6=m26是-椭园
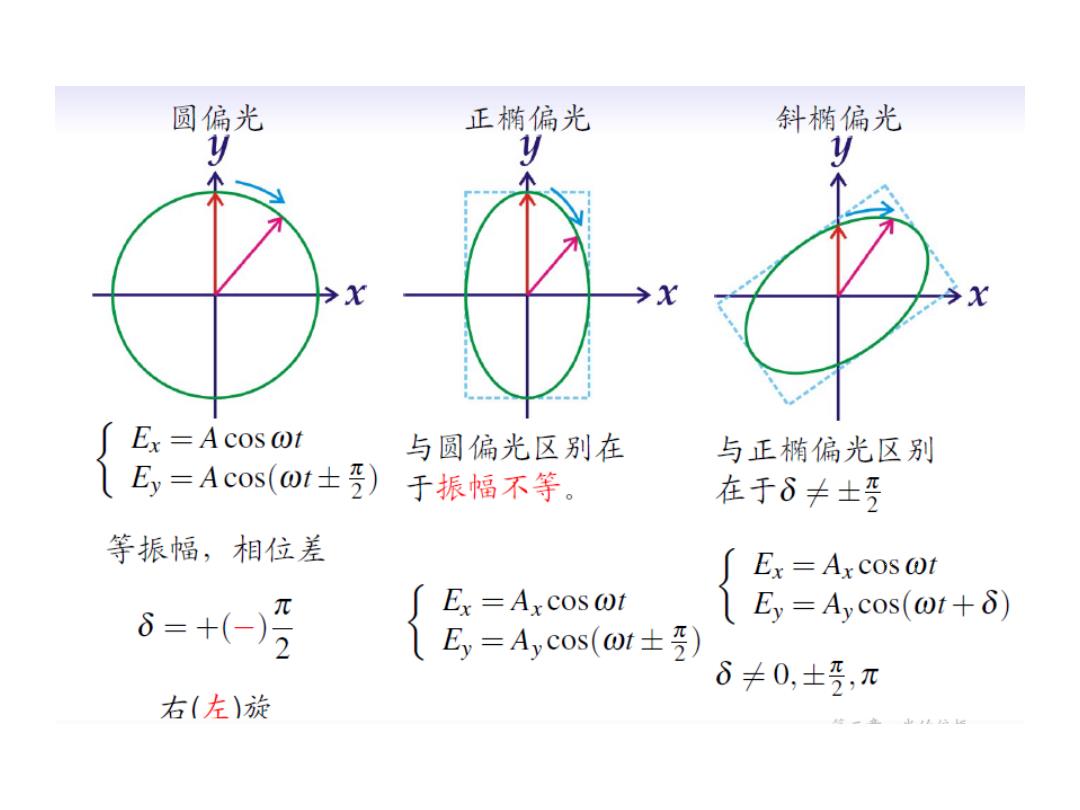
圆偏光 正椭偏光 斜椭偏光 y y y X Ex =Acos @t 与圆偏光区别在 与正椭偏光区别 Ey=Acos(01士) 于振幅不等。 在于δ≠士罗 等振幅,相位差 Ex =Ax cos @t 8=+(-2 Ex=Axcos @t lE,=Ay cos(ot+δ) E=Aycos(Ot士) δ≠0,±5,元 右(左)旋 一金

可见,线偏、圆偏、正椭偏、斜椭偏可用统一的参数方程给出。 究竟是什么偏振态,主要取决于δ。 60 62π/4 6Lπ/2 623π/4 6元 6-π δ=3π/4 6=1π/2 6=-π/4 6⊥0