t分布的概念 1.正态变量X:一般的正态分布X~N(,σ),采用 u=(X-)/σ变换,即变换为标准正态分布:u ≈(0,1)。 2.又因从正态总体抽取的样本均数服从正态分布, 同样可作正态变量的u变换,即有公式: X-L X一4 筒历 返回总目录 返回章目录]口>口结束 第3章总体均数区间估计和假设检验 第15页
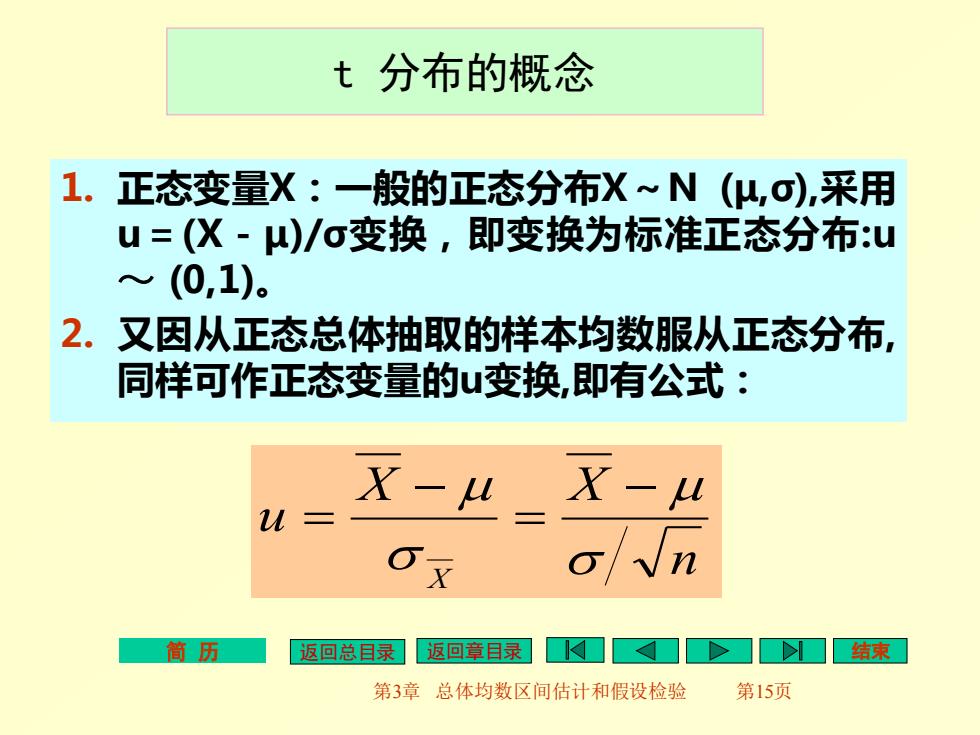
简 历 返回总目录 返回章目录 结束 第3章 总体均数区间估计和假设检验 第15页 1. 正态变量X:一般的正态分布X~N (μ,σ),采用 u=(X-μ)/σ变换,即变换为标准正态分布:u ~ (0,1)。 2. 又因从正态总体抽取的样本均数服从正态分布, 同样可作正态变量的u变换,即有公式: n X X u X − = − = t 分布的概念

3.实际工作中由于总体标准差σ常常未知 故理论的标准误往往未知,而使用样本标准 差S来计算标准误估计值。若用S取代o,此 时就不是u变换而成为t变换了,即有下式。 注意:公式分母中由$代替o。 X一u X-4 Sx S/n 简历 返回总目录 返回章耳录(幻4口>]口结束 第3章总体均数区间估计和假设检验 第16页
简 历 返回总目录 返回章目录 结束 第3章 总体均数区间估计和假设检验 第16页 3. 实际工作中由于总体标准差σ常常未知, 故理论的标准误往往未知,而使用样本标准 差S来计算标准误估计值。若用S取代σ,此 时就不是u变换而成为t变换了,即有下式。 注意:公式分母中由S代替σ。 S n X S X t X − = − =

二、t分布曲线的特征 1.分布曲线是单峰分布,以0为中心,左右两侧对称。 2. 曲线的中间比标准正态曲线(分布曲线)低,两侧翘 得比标准正态曲线略高。 3. t分布曲线随自由度U而变化,当样本含量越小(严格地 说是自由度u=n-1越小),t分布与u分布差别越大: 当U逐渐增大时,t分布逐渐逼近于u分布,当U=∞时, t分布就完全成为正态分布。 4. 分布曲线是一簇曲线,而不是一条曲线。 5. t分布下面积分布规律:根据自由度,查阅分布表得到。 筒历 返回总目录返回章目录口>口结束 第3章总体均数区间估计和假设检验 第17页
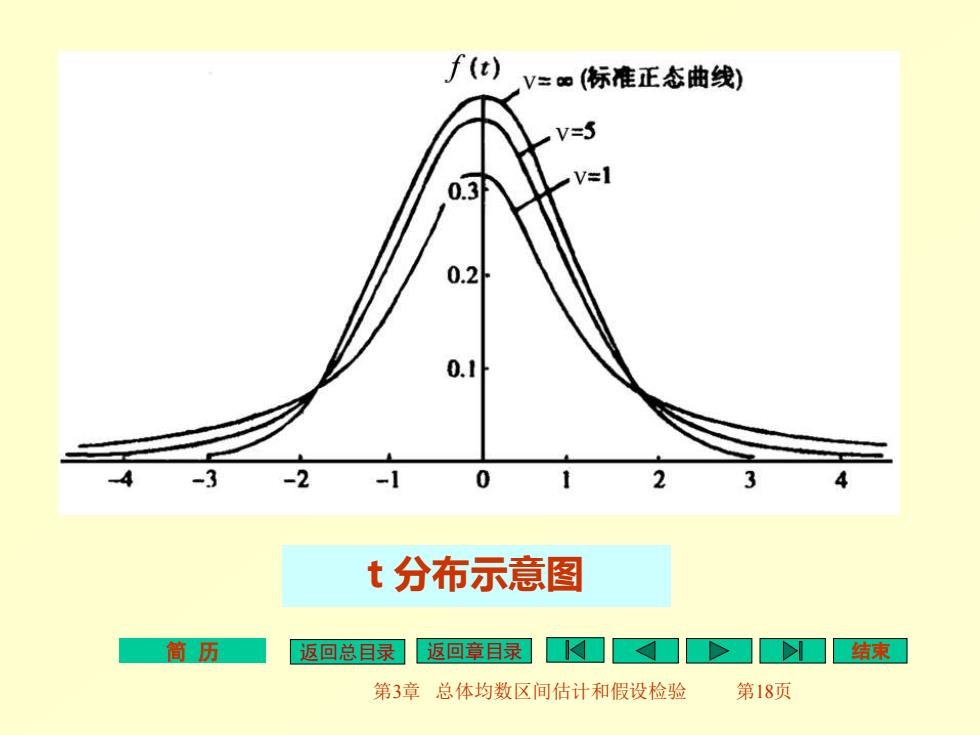
简 历 返回总目录 返回章目录 结束 第3章 总体均数区间估计和假设检验 第17页 二、t 分布曲线的特征 1. t分布曲线是单峰分布,以0为中心,左右两侧对称。 2. 曲线的中间比标准正态曲线(u分布曲线)低,两侧翘 得比标准正态曲线略高。 3. t分布曲线随自由度υ而变化,当样本含量越小(严格地 说是自由度υ =n-1越小),t分布与u分布差别越大; 当υ逐渐增大时,t分布逐渐逼近于u分布,当υ =∞时, t分布就完全成为正态分布 。 4. t分布曲线是一簇曲线,而不是一条曲线。 5. t分布下面积分布规律:根据自由度,查阅t分布表得到
f(t) ,V=m标准正态曲线) V=5 0.3 ,V=1 0.2 0.1 3 -2 0 t分布示意图 简历 返回总目绿 返回章目录4口>]口结束 第3章总体均数区间估计和假设检验 第18页
简 历 返回总目录 返回章目录 结束 第3章 总体均数区间估计和假设检验 第18页 t 分布示意图

t分布曲线下双侧或单侧尾部合计面积 1.我们常把自由度为u的t分布曲线下双侧尾部合 计面积或单侧尾部面积指定值为α。 2.横轴上相应的t界值记为t。u。如当U=20 =0.05时,记为t0.05,20;当v=22,c=0.01时 记为to.01,22对于tu值,可根据c和u值,查附 表2,界值表。 筒历 返回总目录返回章目录口>]口结束 第3章总体均数区间估计和假设检验 第19页
简 历 返回总目录 返回章目录 结束 第3章 总体均数区间估计和假设检验 第19页 t分布曲线下双侧或单侧尾部合计面积 1. 我们常把自由度为υ的t分布曲线下双侧尾部合 计面积或单侧尾部面积指定值为α。 2. 横轴上相应的t界值记为tα,υ。如当υ=20, α=0.05时,记为t0.05,20;当υ=22,α=0.01时, 记为t0.01,22。对于tα,υ值,可根据α和υ值,查附 表2,t界值表