
Sec.1.3 Frequency Concepts in Continuous-Discrete-Time Signals 15 The analog sinusoidal signal in(1.3.3)is characterized by the following prop- erties: A1.For every fixed value of the frequency F.x(r)is periodic.Indeed.it can easily be shown,using elementary trigonometry.that xa(1+Tp)=xo(t) where T=1/F is the fundamental period of the sinusoidal signal. A2.Continuous-time sinusoidal signals with distinct (different)frequencies are themselves distinct. A3.Increasing the frequency F results in an increase in the rate of oscillation of the signal,in the sense that more periods are included in a given time interval. We observe that for F =0.the value T=oc is consistent with the fun- damental relation F =1/T.Due to continuity of the time variable t,we can increase the frequency F.without limit.with a corresponding increase in the rate of oscillation. The rclationships we have described for sinusoidal signals carry over to the class of complex exponential signals Xu(1)Ae(r+6) (1.3.4 This can easily be seen by expressing these signals in terms of sinusoids using the Euler identity e±=cos中去j5inφ (1.3.5) By definition,frequency is an inherently positive physical quantity.This is obvious if we interpret frequency as the number of cycles per unit time in a periodic signal.However.in many cases.only for mathematical convenience.we need to introduce negative frequencies.To see this we recall that the sinusoidal signal (1.3.1)may be expressed as 无0)=Acos(+0j=e+cm9 (1.3.6 which follows from(1.3.5).Note that a sinusoidal signal can be obtained by adding two equal-amplitude complex-conjugate exponential signals,sometimes called pha- sors,illustrated in Fig.1.11.As time progresses the phasors rotate in opposite directions with angular frequencies radians per second.Since a positive fre- quency corresponds to counterclockwise uniform angular motion,a negative fre- quency simply corresponds to clockwise angular motion. For mathematical convenience,we use both negative and positive frequencies throughout this book.Hence the frequency range for analog sinusoids is -oo< F <OC

16 Introduction Chap.1 Im AR 2r+日 Re 2!+9 Figure 1.11 Representation of a cosine function by a pair of complex-conjugate exponentials (phasors). 1.3.2 Discrete-Time Sinusoidal Signals A discrete-time sinusoidal signal may be expressed as x(n)=Ac05{n+B),-<H<X 1.3.7) where n is an integer variable.called the sample number.A is the amplitude of the sinusoid.is the frequency in radians per sample.and 6 is the phase in radians. If instead of w we use the frequency variable f defined by 仙wm2rf (1.3.8 the relation (1.3.7)becomes x(n)=A cos(2nfn +).-xc<n<oc 1.3.9) The frequency f has dimensions of cycles per sample.In Section 1.4.where we consider the sampiing of analog sinusoids,we relate the frequency variable f of a discrete-time sinusoid to the frequency F in cycles per second for the analog sinusoid.For the moment we consider the discrete-time sinusoid in (1.3.7) independently of the continuous-time sinusoid given in (1.3.1).Figure 1.12 shows a sinusoid with frequency =/6 radians per sample (f=cycles per sample) and phase =/3. n=A costa + Figure 1.12 Example of a discrele-time sinusoida!signal (ca/6 and &=3)

Sec.1.3 Frequency Concepts in Continuous-Discrete-Time Signals 17 In contrast to continuous-time sinusoids.the discrete-time sinusoids are char- acterized by the following properties: B1.A discrete-time sinusoid is periodic only if its frequency f is a rational number. By definition.a discrete-time signal x(n)is periodic with period N(N>0)if and only if x(nN)=x(n)for all n (1.3.10) The smallest value of N for which (1.3.10)is true is called the fundamental period. The proof of the periodicity property is simple.For a sinusoid with frequency fo to be periodic.we should have cos 27foN+n)+=cos(2 fon +6) This relation is true if and only if there exists an integer such that 2tfnN=2k元 or.equivalently. 加=N 1.3.11) According to (1.3.11).a discrete-time sinusoidal signal is periodic only if its fre- quency f can be expressed as the ratio of two integers (i.e..fo is rational). To determine the fundamental period N of a periodic sinusoid.we express its frequency fo as in (1.3.11)and cancel common factors so that k and N are relatively prime.Then the fundamental period of the sinusoid is equal to N.Observe that a small change in frequency can result in a large change in the period.For example. note that f=31/60 implies that N =60.whereasf=30/60 results in N2 =2. B2.Discrete-time sinusoids whose frequencies are separated by an integer multiple of 2n are identical. To prove this assertion.let us consider the sinusoid cos(on+).It easily follows that cos[(+2n]=cos(amn +2in+e)cos(won + (1.3.12) As a result.all sinusoidal sequences x(n)=A cos(wn+). k=0.1.2... (1.3.13) where =0+2kr. -开≤的≤π are indistinguishable (i.e.,identical).On the other hand,the sequences of any two sinusoids with frequencies in the range-π≤w≤ror-i≤J≤are distinct.. Consequently,discrete-time sinusoidal signais with frequencies ls orfs
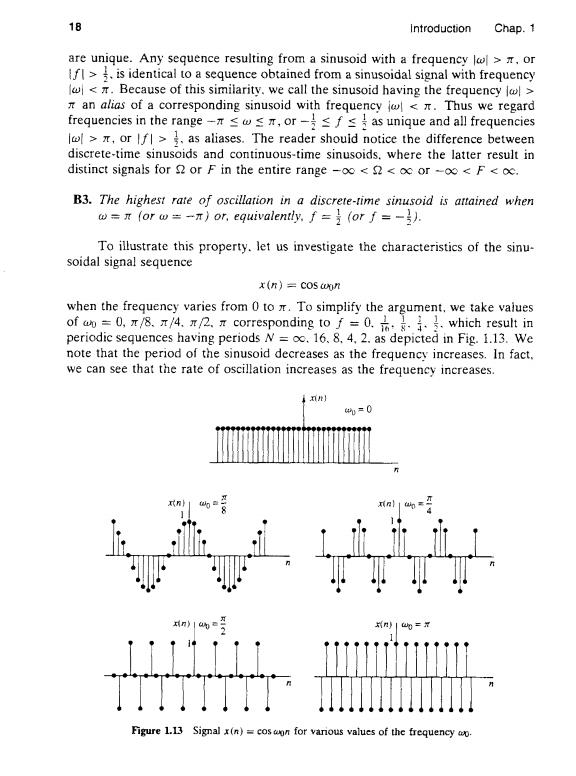
18 Introduction Chap.1 are unique.Any sequence resulting from a sinusoid with a frequency lo>or f>.is identical to a sequence obtained from a sinusoidal signal with frequency <Because of this similarity.we call the sinusoid having the frequency> x an alias of a corresponding sinusoid with frequency il x.Thus we regard frequencies in the range-T≤w≤r,or-≤fs是as unique and all frequencies >orf>as aliases.The reader shouid notice the difference between discrete-time sinusoids and continuous-time sinusoids.where the latter result in distinct signals for n or F in the entire range -oc<n<oc or -o0<F<oc. B3.The highest rate of oscillation in a discrete-time sinusoid is attained when w=(or w=-n)or.equivalently.f=(orf=-3). To illustrate this property.let us investigate the characteristics of the sinu- soidal signal sequence x(n)cosn when the frequency varies from 0 to x.To simplify the argument,we take values ofw=0,π,/8.rf4.πf2.corresponding to f=0.六,..}、which result in periodic sequences having periods N =oo.16.8.4.2.as depicted in Fig.1.13.We note that the period of the sinusoid decreases as the frequency increases.In fact. we can see that the rate of oscillation increases as the frequency increases. } %=0 n 可n1h= n|= 州n)|0三 Figure 1.13 Signal x(n)=cos con for various values of the frequency wo

Sec.1.3 Frequency Concepts in Continuous-Discrete-Time Signals 19 To see what happens for rs wo s 2n.we consider the sinusoids with frequencies w =u and c=27-wp.Note that as w varies from to 27.w varies from a to 0.It can be easily seen that x1(n〉=A coSw]n=AC0sD力 2(n)=A cos wn A cos(2 -wu) (1.3.14) =A cos(-n)=() Hence is an alias of If we had used a sine function instead of a cosine func- tion,the result would basically be the same.except for a 180 phase difference between the sinusoidsx(n)and x2(n).In any case.as we increase the relative frequency wu of a discrete-time sinusoid from x to 2.its rate of oscillation de- creases.For w =2n the result is a constant signal.as in the case for =0. Obviously.for w=(or f=)we have the highest rate of oscillation. As for the case of continuous-time signals.negative frequencies can be in- troduced as well for discrete-time signals.For this purpose we use the identity A Xn)=Acos(om+A=号e++ 1.3.151 Since discrete-time sinusoidal signals with frequencies that are separated by an integer multiple of 2 are identical.it follows that the frequencies in any interval wsww+2 constitute all the existing discrete-time sinusoids or complex exponentials.Hence the frequency range for discrete-time sinusoids is finite with duration2r,Usually.we choose the range0≤w≤2ror-r≤w≤z(0≤f≤1. -≤f≤),which we call the fundamental range. 1.3.3 Harmonically Related Complex Exponentials Sinusoidal signals and complex exponentials play a major role in the analysis of signals and systems.In some cases we deal with sets of harmonically related com- plex exponentials (or sinusoids).These are sets of periodic complex exponentials with fundamental frequencies that are multiples of a single positive frequency. Although we confine our discussion to complex exponentials.the same proper- ties clearly hold for sinusoidal signals.We consider harmonically related complex exponentials in both continuous time and discrete time. Continuous-time exponentials.The basic signals for continuous-time. harmonically related exponentials are sk(t)=eikdor =e)2nkFor k=0.±1.土2.., (1.3.16) We note that for each value of k.s(r)is periodic with fundamental period 1/(k Fo)=T/k or fundamental frequency k Fo.Since a signal that is periodic with period T/k is also periodic with period k(T/k)=T for any positive integer k,we see that all of the se(r)have a common period of Te.Furthermore,according