
赋权图和距离 (赋权)长度 ● 经过的边的权和 ■ 最短路 3 ■距离 2 VA V6 ■离心率 ■中心点 ■半径 ■中心 ■ 边缘点 ■直径 2023/4/10 11
n (赋权)长度 l 经过的边的权和 n 最短路 n 距离 于连通赋权图 G = < V, E, w> , 距离函数dist满足三角不等式吗: n 离心率 n 中心点 n 半径 n 中心 n 边缘点 n 直径 2023/4/10 11 赋权图和距离

赋权图和距离 (赋权)长度 ·经过的边的权和 ■最短路 ■距离 ●对于连通赋权图G=<V,E,w>, 距离函数it满足三角不等式吗: u,u,weV,dist(u,v)+dist(u,w)≥dist(u,w) ■ 离心率 ■中心点 ■半径 ■ 中心 ■ 边缘点 ■直径 2023/4/10 12
n (赋权)长度 l 经过的边的权和 n 最短路 n 距离 l 对于连通赋权图G = <V, E, w>, 距离函数dist满足三角不等式吗: n 离心率 n 中心点 n 半径 n 中心 n 边缘点 n 直径 2023/4/10 12 赋权图和距离

赋权图和距离 ■如何计算两个顶点间的距离? ■如何计算一个顶点和赋权图中所有顶点间的距离? ■ 戴克斯特拉算法 (只适用于边权非负的赋权图) 算法6.1:戴克斯特拉算法 输人:赋权图G=(,E,w),顶点u 初值:V中所有顶点的d初值为o;Q初值为V 1u.d←0: 2 while Q≠0do sv←-argmin.d wEO Q←-Q\{v; foreach(v,w)∈Edo if w.d>v.d +w((v,w))then w.d←u.d+w(u,w)月 2023/4/10 13
n 如何计算两个顶点间的距离? n 如何计算一个顶点和赋权图中所有顶点间的距离? n 戴克斯特拉算法 (只适用于边权非负的赋权图) 2023/4/10 13 赋权图和距离

本次课的主要内容 6.1赋权图和距离 6.2最小生成树 6.3赋权欧拉图 6.4赋权哈密尔顿图 7.1有向图的定义 72有向图的表示 7.3有向图的连通 7.4有向图的距离 7.5流网络和最大流 2023/4/10 14
6.1 赋权图和距离 6.2 最小生成树 6.3 赋权欧拉图 6.4 赋权哈密尔顿图 7.1 有向图的定义 7.2 有向图的表示 7.3 有向图的连通 7.4 有向图的距离 7.5 流网络和最大流 2023/4/10 14 本次课的主要内容
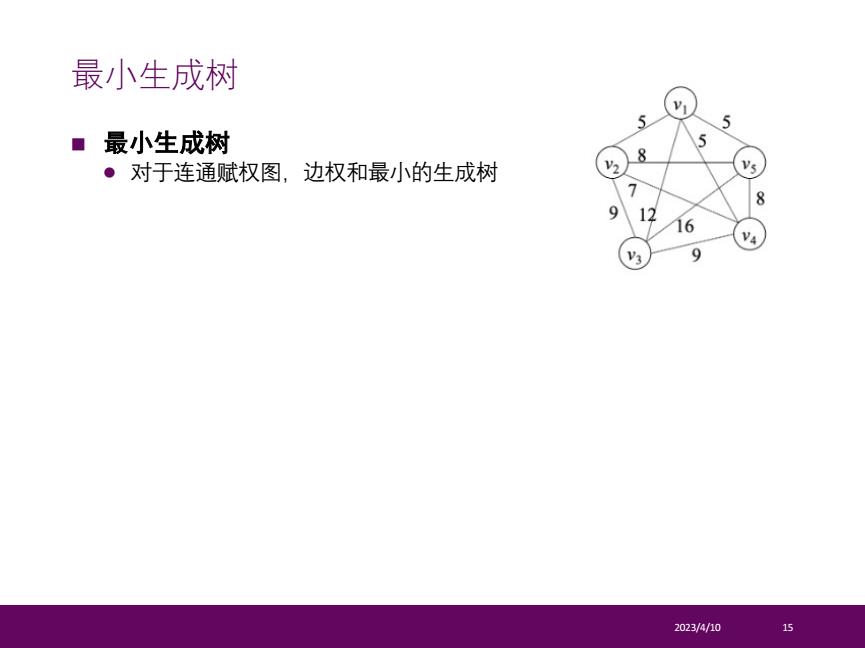
最小生成树 ■最小生成树 8 ·对于连通赋权图,边权和最小的生成树 Vs 12 16 V4 9 2023/4/10 15
n 最小生成树 l 对于连通赋权图,边权和最小的生成树 2023/4/10 15 最小生成树