电子科技大学：《无线系统中的微波与射频 Microwave and RF Design in Wireless Systems》课程教学资源（课件讲稿）ch05 Filter

●●● ●●●● ●●●●心 ●●●● 1.Characterization by Power Loss Ratio ●●●● ●●●● ●●●● ●● Power Loss ratio:P 1-r(o IL(dB)=101g PLR Because of the causal properties of networks由于网s络的 因果关系，T(o)2 is an even function偶函数ofo(see Problem 5.1), Therefore,writing|T(o)l2 as a polynomial多项式ino2 of-i两 M(o2) M(O) PR=1+ N(o2） 6

1. Characterization by Power Loss Ratio Power Loss ratio: Because of the causal properties of networks由于网络的 因果关系,  2 is an even function偶函数of  (see Problem 5.1), Therefore, writing  2 as a polynomial多项式 in  2 6   2 1 1 in LR Load P P P        10lg L R IL dB P        2 2 2 2 M M N            2 2 1 LR M P N    

●●● ●●●● ●●●●心 ●●●0 Maximally flat response (Butterworth) ●●●● ●●●● ●●●● ●● where N is the order of the filter 2N PLR =1+k2 滤波器的阶数 @is the cutoff frequency截止频率 Passband::o=0~o。 The power loss ratio at the band edge @c: PIR=1+k2 IF k=1,then PLR=3dB 2N FOr0>0。PR≈k2 0 7

Maximally flat response (Butterworth) where N is the order of the filter 滤波器的阶数  c is the cutoff frequency截止频率 Passband: The power loss ratio at the band edge c: IF k=1, then PLR=3dB 7 2 2 1 N LR c P k           c   0 ~  2 1 P k LR   For   c 2 2 N LR c P k         

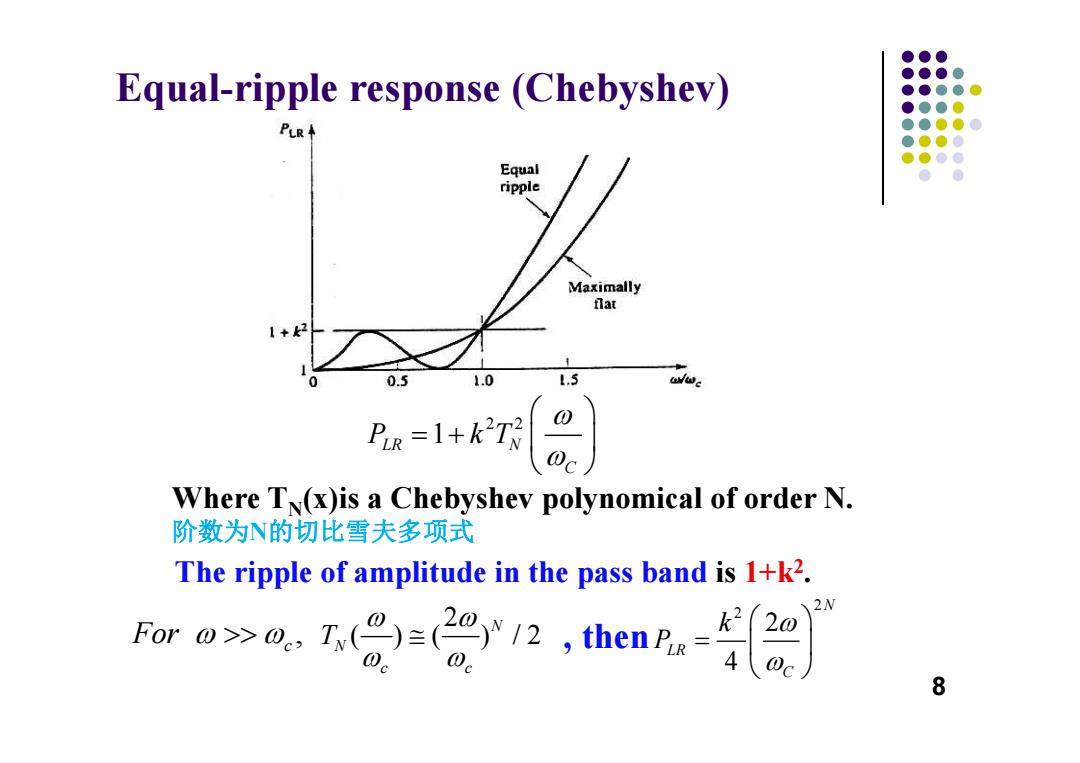
●●● Equal-ripple response (Chebyshev) ●●●● ●●●●● ●●●0 PLR ●●●●0 ●●●0 ●●●● Equal ● ripple Maximally flat +2 0.5 1.0 1.5 PiR=1+k2T Where T(x)is a Chebyshev polynomical of order N. 阶数为N的切比雪夫多项式 The ripple of amplitude in the pass band is 1+k2. w0.g2r2,c.2） 2N 8

Equal-ripple response (Chebyshev) Where T N(x)is a Chebyshev polynomical of order N. 阶数为 N的切比雪夫多项式 The ripple of amplitude in the pass band is 1+k 2. , then 8 2 2 1 LR N C P kT           , For   c 2 ( ) ( ) /2 N N c c T      2 2 2 4 N LR C k P         

●●● ●●●● ●●●●● ●●●0 ●●●●0 ●●●0 Linear phase response:线性相位响应 ●●●● ● o创al+r川 The group delay群延时 0ex+n8 a maximally flat function. 9

Linear phase response:线性相位响应 The group delay群延时 →a maximally flat function. 9   2 1 N C A P                       2 1 21 N C d A PN d                     

To conclude-1 ●●● ●●●● ●●●●● ●●●0 S 4.3 Antenna noise temperature ●●●● ●●●0 ●●● ● ● Brightness Anteen temperature tempenta Background To Attenuator temperature Tp Tg (0.) Ideal antenna L=刘 (e=I) T +(L-1)Tp T4= =emTs+(1-eu)Tr Tp:physical temperature of antenna; L TB:background temperature; Th= ()sinOdod temprature )sin0d0dp J0=0 GP 9%=10ε号(9 N,kT BLs kBLs For a receiver:T=T+TLNE 10

To conclude - 1 §4.3 Antenna noise temperature Tp: physical temperature of antenna; TB: background temperature; Tb: Brightness temperature For a receiver: 10     1 1 b P A rad b rad P TLT T eT e T L           2 0 0 2 0 0 , , sin , sin B b T D dd T D dd                              10log   A G G dB dB T K T  i t rt tt r i AS A S S GG P GP G N kT BL T kBL         TTT e A LNB  