
省领精品课程—一材料力学 D.=D.=0.C=C:-(6F-(-a)-P(F-B) (w) 将(w)式代回到m小、(、(q、()四式,得到转角和挠度方程。 AC段,(0sx≤a) 以告0-6-3) (w) (x) CB段(asxs) a以0-8-3)+5-o ,告0-8-)片- 61 现在来分析所得到的解。 (1)关于最大转角。当没有异号的弯矩时,简支染的最大转角发生在支座处。在(w) 式中令=0,在式)冲令,=1,得到 Pb g=监6+2*五0-a*o 当a>b时,|日。最大,即离P力较近的支座截面的转角(指绝对)最大。 (2)关于最大挠度。由上面的计算可看到,日,和日。符合相反,因此跨中一定有一点 的日-0,它对应于y·至于这一点在哪一段梁上,还应求出日.再判断。(w)式中 =a,得0.欲-0 若ab,则日.为负,与Q:反号,这时0-0的截面必在AC段,即在大于2的那一段内。 令()式等于零,得发生最大挠度的截面位置: P-6 (a>b时) 代入(x)式得到最大挠度 -可ab Ph 17 This document is generated by trial version of Print2Flash(www.printflash.com)

省级精品课程—材料力学 特别地,当集中力P在跨中时,abV2由此得到 P x=3ym48l (3)关于最大挠度的近似值。当集中力P偏离跨中,最大挠度y与跨中的挠度相差 多少呢?在()式中,令书子得到 (a>b时) 比较y与跨中挠度,用相对误差表示,记 8=Yms-yihom 当b=2时,yx=y,6=0随者力P偏离跨中越多,6增大。考虑极端情况,当b→0 Pb产 11 时,63弘48 32 PbP ,gf16=257% 5E1 5 由此可见,在简支梁中,只要挠曲线上无拐点用跨中的挠度代替最大挠度不会引起很大误差。 积分法是计算染的位移的基本方法,它可以给出任意截面的转角和挠度,但一般来说计 算比较冗长。 §9.3用叠加法求梁的转角和挠度 由于我们研究小变形,且梁的材料服从虎克定律(即工作在线弹性范围内),则梁的位 移与梁上的载荷成线性关系。在这个条件下,当梁上同时有几个载荷作用时,某一截面的转 角或挠度等于每一个载荷单独作用时引起的转角或挠度的代数和。根据这个原理求转角或挠 度的方法称为叠加法。 显然,应用叠加法有个前提条件:即单个载荷作用下梁的位移是已知的,只有这祥,才 显示出叠加法的优越性。表91列出了几种简单载荷作用下染的转角和挠度,以便于应用, 吾加法常用干计算指定截面的转角和挠度 下面举例说明叠加法的原理及其应用技巧 例9-3计算图示荷支梁的转角0,和挠度y。,设抗弯刚度E为已知的常数 This document is generated by trial version of Print2Flash(www.print2flash.com)

省领精品课程一材料力学 解:利用表-1的第6项,在D处的P力作用下,日,P0-四21-a) 6EI1 在F处的P力作用下,O,Pa0-A+a 6El1 于是在D、F两处的P力共同作用下 在F处的P力作用下,设-a>0即2a,这个条件满足,故 戈台- 于是在D、F两处的P力共同作用下,由对称性得 =2品-品e-4的 例94计算图示悬梁自由端的挠度y,己知E为常数 题94图 解:利用表91第2项。将分布载荷看作是一系列微小集中力之和。在微小集中力作用下, dvs-ET 31-x)acs 放在分布载荷作用下 为品r-盼 例95求图(a)所示简支梁跨中的挠度y。已知E团为常数. 解:图(a)中的y.可看作图(b)中的y和图(c)中的y2的代数和 5g' 已知38瓦。由对称性,当AC段有我背q与B段有问样载荷▣时跨中的挠度是相 179 This document is generated by trial version of Print2Flash(www.printflash.com)
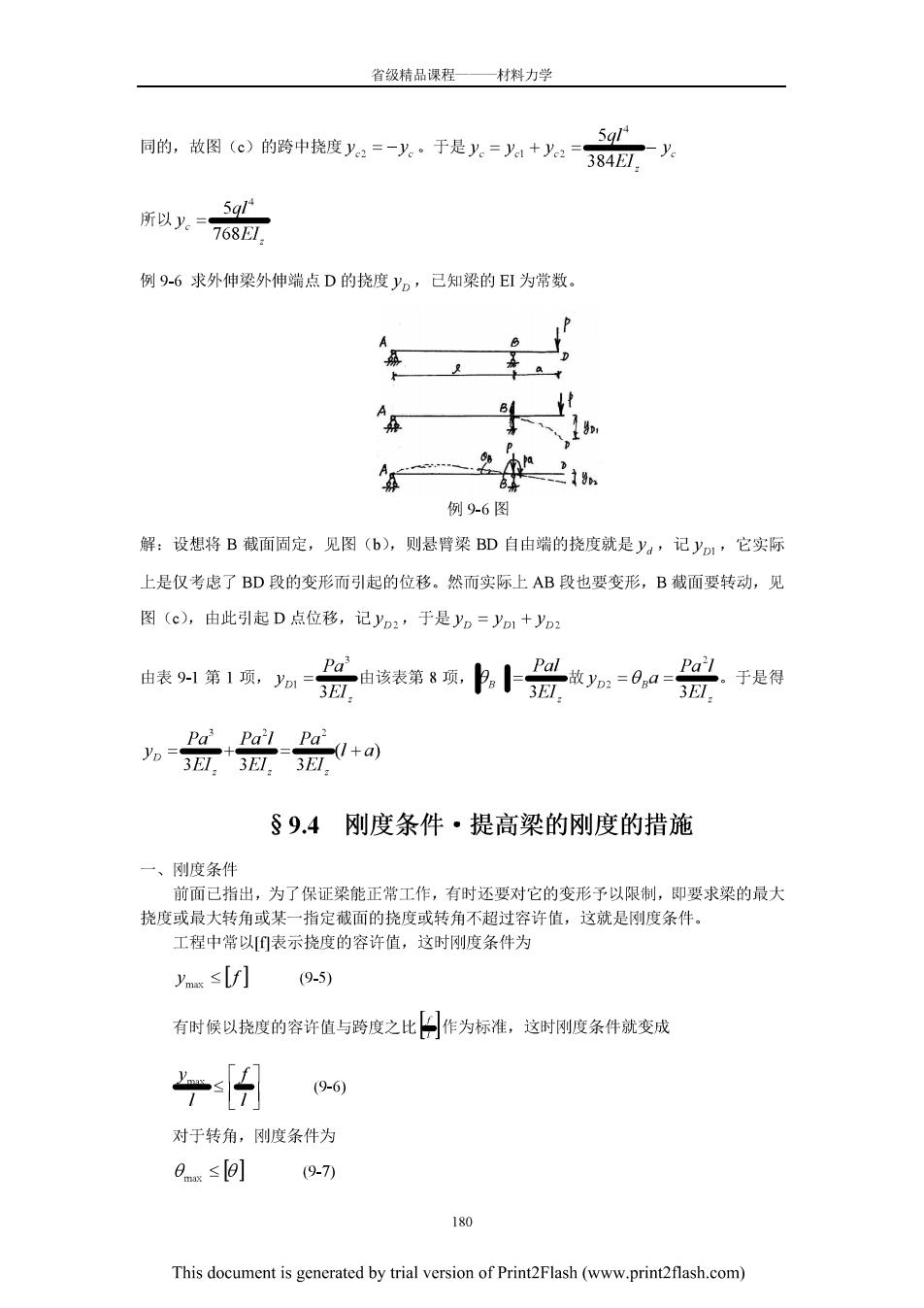
省领精品课程一材料力学 同的,故图(®)的跨中挠度a=-火·于是。=h+:一384可少 5aP 所以y.=768EL: 例9-6求外伸梁外伸端点D的挠度yD,已知梁的EI为常数。 例9-6图 解:设想将B截面固定,见图(b),则悬臂梁BD自由端的挠度就是y,记yo,它实际 上是仅考虑了BD段的变形而引起的位移。然而实际上AB段也要变形,B截面要转动,见 图(),由此引起D点位移,记yo2,于是yn=yo1+yo: 自装第1现a合曲读装第8现.|合a=8如哥于是 §9.4刚度条件·提高梁的刚度的措施 一、刚度条件 前面已指出,为了保证梁能正常工作,有时还要对它的变形予以限制,即要求染的最大 挠度或最大转角或某一指定酸面的挠度或转角不超过容许值,这就是刚度条件。 工程中常以表示挠度的容许值,这时俐度条件为 mss[/]9-5) 有时候以挠度的容许值与跨度之比口作为标准,这时刚度条件就变成 一H 9-6) 对于转角,刚度条件为 0msg9-7刀 0 This document is generated by trial version of Print2Flash(www.print2flash.com)

省级精品课程 材料力学 各类工程问题中,对旧和[]都有具体规定,例如铁路钢桥=女一女,普通机床主 轴,月-★点=0.005-0.001ad. 例9-7吊车大桑由45a工字钢制成,已知梁的容许挠度日=女,材料的弹性模量 +细 E=200GPa,试校核吊车梁的刚度。 例9-7图 解:当吊重在跨中时,跨中的挠度最大。若考虑梁的自重,则 p 5g' yos=48E1.384El. 103 50x105x788x10 200×10°×32240×1048 384 =15.5×10(1042+1026) =17.7×103m=17.7mm 177 10 二品 故刚度条件满足。 二、提高染的刚度的措施 公式(8-1)或者表91的最后一列可看到,梁的变形或位移与弯矩M(包括载荷 跨度等 以及抗弯刚度E有关。因此,为了减少梁的变形,就应在这两个方面采取措枪 1.减小弯矩的绝对值。如改变支座位置,尽可能使集中力靠近支座,分散集中力,缩 小跨度,改变结构形式等提高梁的强度的措施在这里原则上也都适用。 2.增大抗弯刚度。这主婴靠采用合理截面形状,增大截面的惯性矩z来实现。以钢为 例,各种钢材的弹性模量E值比较接近,因此靠增大E来增大抗弯刚度Ez的办法意义不 大多数情况下,提高梁的强度的措施与提高梁的刚度的措施原则上是一致的。然而两老 又有区别。首先,染的较大正应力只决定于该截面的较大弯矩,因此仅将局部截面增大,即 采用变截面梁,即可提高梁的强度。但梁某一指定藏面的位移却与整个梁的变形有关,因此 为了减小位移,提高梁的刚度,必须使整个梁的变形减小。图94(a)为一悬臂梁,固定端 截面的弯矩MA=P!最大,最大正应力也在该截面上,它其有局部性。自由端截面的弯矩 MB=O,但该截面的挠度B为最大, 是B截面 局部变形的表 是整个梁变 形的表现。其次,由于上面的原因,当采取某个措施时,强度提高的程度与刚度提高的程度 差别很大。比较图94(a)和(b),若将悬臂梁的跨度减少一半,其余情况不变,则最大正 This document is generated by trial version of Print2Flash(www.printflash.com)