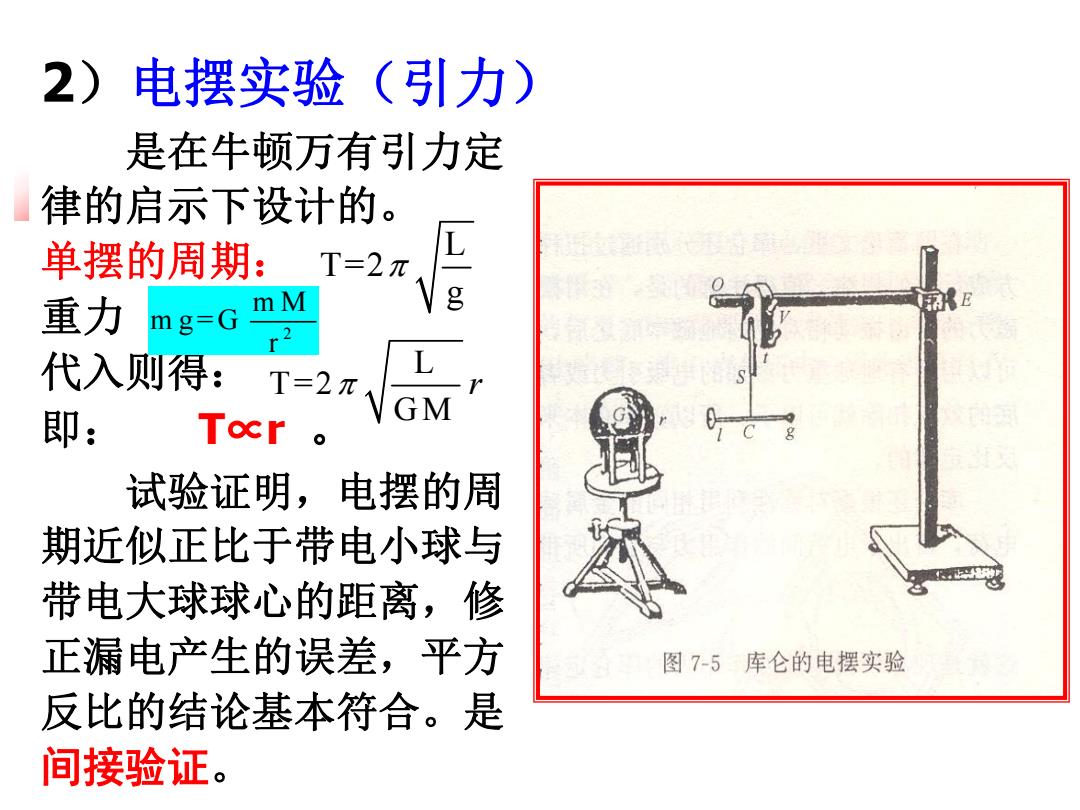
2)电摆实验(引力) 是在牛顿万有引力定 律的启示下设计的。 单摆的周期:T=2π, 重力mg=G mM E 代入则得: T=2π L 即: Tocr |GM .o 试验证明,电摆的周 期近似正比于带电小球与 带电大球球心的距离,修 正漏电产生的误差,平方 图7-5库仑的电摆实验 反比的结论基本符合。是 间接验证
2)电摆实验(引力) 是在牛顿万有引力定 律的启示下设计的。 单摆的周期: 重力 代入则得: 即: T∝r 。 试验证明,电摆的周 期近似正比于带电小球与 带电大球球心的距离,修 正漏电产生的误差,平方 反比的结论基本符合。是 间接验证。 L T=2 g 2 m M m g= G r L T=2 GM r

3.库仑定律 库仑定律的精确表述是: 两个静止的点电荷q和q1之间的作用力 的大小与两点电荷电量的乘积成正比,与 它们之间距离的平方成反比,作用力的方 向沿着两点电荷间的连线,同号电荷相斥, 异号电荷相吸
3. 库仑定律 库仑定律的精确表述是: 两个静止的点电荷q0和q1之间的作用力 的大小与两点电荷电量的乘积成正比,与 它们之间距离的平方成反比,作用力的方 向沿着两点电荷间的连线,同号电荷相斥, 异号电荷相吸
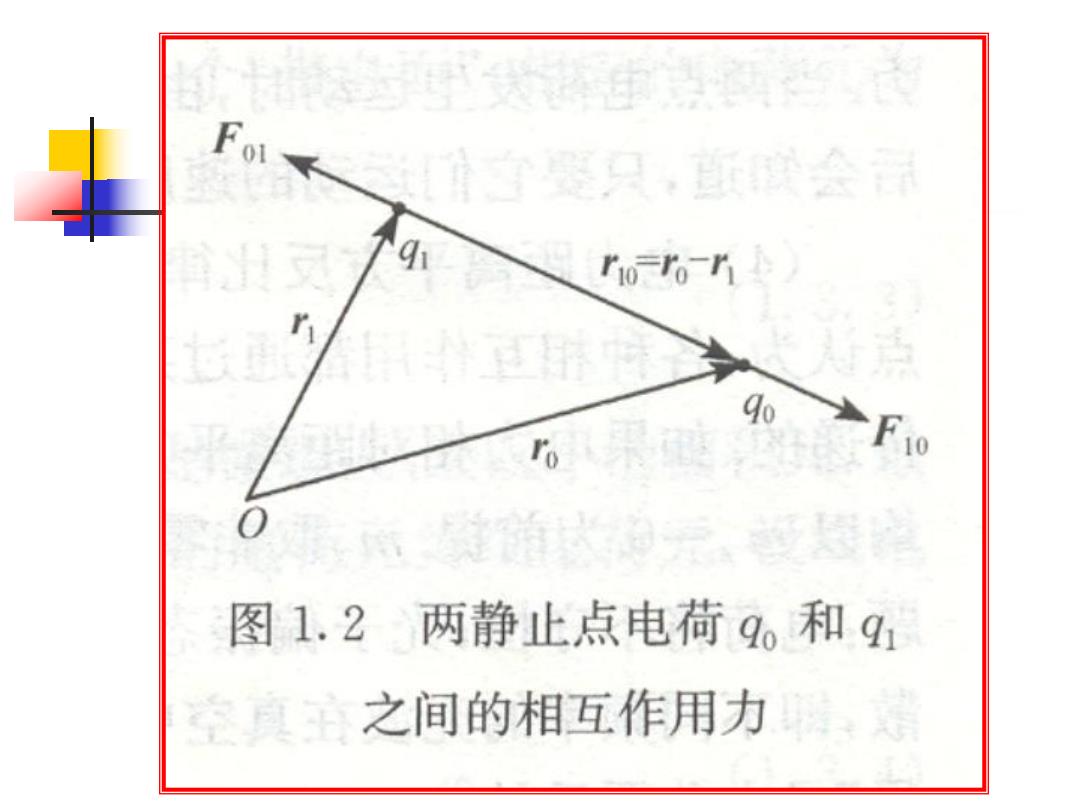
竖只,所联会 ro ro n r 90 ro 产F0 图1.2两静止点电荷9。和91 空真 之间的相互作用力

按图1.2,可将库仑定律表达为: 0=k。= (1.2.1) k为比例常数,由实验测定并与单位制有关。 我们取国际单位制(S工),在真空中,我们将常数 k写成为k=1/(4πE0)其中8,称为真空介电常量 或电容率 由实验测定已知电量的两个点电荷在真空中的相 互作用力,便可得k或8。! 的值。近似值为: ≈8.85×102C2.N1.m-2 相应的k值为: k≈8.99×109C-2.Nm2
按图1.2,可将库仑定律表达为: k 为比例常数,由实验测定并与单位制有关。 我们取国际单位制(SI),在真空中,我们将常数 k 写成为 ,其中 称为真空介电常量 或电容率。 由实验测定已知电量的两个点电荷在真空中的相 互作用力,便可得k 或 的值。近似值为: 相应的k 值为: 1 0 10 3 10 01 10 , q q k r F r F 0 (1.2.1) 0 k 1 / (4 ) 12 2 1 2 0 8.85 10 C N m 9 2 2 8.9910 C N m k 0

4.对库仑定律的几点说明 (1)库仑定律适用的对象是点电荷。点电荷意即其 尺度为零,是种模型。自然界中并不存在这种理 想的点电荷。在实际问题中,只要两带电体的尺 度远小于它们之间的距离,就可忽略带电体本身 的尺度,而把它们当作点电荷来处理 (2)库仑定律只适用于两点电荷静止的情况,因此 人们常把库仑力称为静电力。当两点电荷发生运 动时,由库仑定律所预言的相互作用力应该进行 修改。但以后会知道,只要它们运动的速度远低 于光速,这一修改可以忽略
4. 对库仑定律的几点说明 (1) 库仑定律适用的对象是点电荷。点电荷意即其 尺度为零,是种模型。自然界中并不存在这种理 想的点电荷。在实际问题中,只要两带电体的尺 度远小于它们之间的距离,就可忽略带电体本身 的尺度,而把它们当作点电荷来处理。 (2) 库仑定律只适用于两点电荷静止的情况,因此 人们常把库仑力称为静电力。当两点电荷发生运 动时,由库仑定律所预言的相互作用力应该进行 修改。但以后会知道,只要它们运动的速度远低 于光速,这一修改可以忽略