
同度量因秦的作用 例如:研究多种商品销售量和销售价格的综合变动情况 当研究销售量的变动时,销售量是数量指标,则与 之相联系的质量指标一价格,就是同度量因素 ∑(商品销售量×商品销售价格)=商品销售总额 所研究的指数化指标 同度量因素 价值量指标 当研究价格的变动时,商品价格是质量指标,则与 之相联系的数量指标销售量,就是同度量因素 ∑(商品销售量×商品销售价格)=商品销售总额 同度量因素 所研究的指数化指标 价值量指标
同度量因素的作用 当研究销售量的变动时,销售量是数量指标,则与 之相联系的质量指标——价格,就是同度量因素 当研究价格的变动时,商品价格是质量指标,则与 之相联系的数量指标——销售量,就是同度量因素 例如:研究多种商品销售量和销售价格的综合变动情况 (商品销售量 × 商品销售价格)= 商品销售总额 所研究的指数化指标 同度量因素 ∑ 价值量指标 (商品销售量 × ∑ 商品销售价格)= 商品销售总额 同度量因素 所研究的指数化指标 价值量指标

2、对比 通过解决同度量因素的时期,来解 决对比的问题。 指数分析是利用价值量指标的形式,分析其中的数量指标 或质量指标的综合变动,分析的方法就是将引进的同度量 因素的时期固定,即假定同度量因素不变,从而通过对比 反映所研究指标的变动情况。 如前例:设:销售量为q,价格为p, 下标1表示报告期,0表示基期 反映多种商品销鲁量变动的指数公式有: ∑9Po ∑4P ∑9oP ∑gp, ∑9P, 拉氏指数 帕氏指数 不变价指数
2、对比 通过解决同度量因素的时期,来解 决对比的问题。 指数分析是利用价值量指标的形式,分析其中的数量指标 或质量指标的综合变动,分析的方法就是将引进的同度量 因素的时期固定,即假定同度量因素不变,从而通过对比 反映所研究指标的变动情况。 如前例: 下标 表示报告期,表示基期 设:销售量为 ,价格为 , 1 0 q p 反映多种商品销售量变动的指数公式有: 0 0 1 0 q p q p 0 1 1 1 q p q p n n q p q p 0 1 拉氏指数 帕氏指数 不变价指数 √
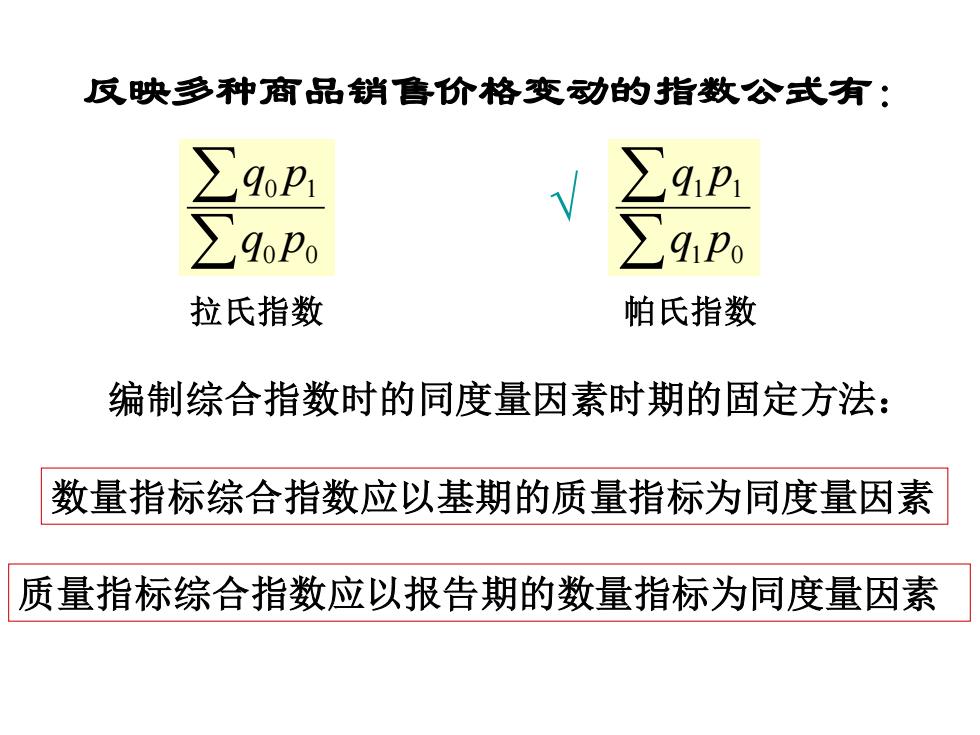
反映多种商品销价格变动的指数公式有: ∑9op1 ∑goP0 ∑9p 拉氏指数 帕氏指数 编制综合指数时的同度量因素时期的固定方法: 数量指标综合指数应以基期的质量指标为同度量因素 质量指标综合指数应以报告期的数量指标为同度量因素
反映多种商品销售价格变动的指数公式有: 0 0 0 1 q p q p 1 0 1 1 q p q p 拉氏指数 帕氏指数 √ 编制综合指数时的同度量因素时期的固定方法: 数量指标综合指数应以基期的质量指标为同度量因素 质量指标综合指数应以报告期的数量指标为同度量因素

即:当所研究的指数化指标为数量指标时,称为数 量指标综合指数,其同度量因素为基期质量指标。 数量指标综合指数: 当所研究的指数化指标为质量指标时,称为质量 指标综合指数,其同度量因素为报告期数量指标。 质量指标综合指数: 公式中:q代表数量指标,p代表质量指标 下标1代表报告期,0代表基期
数量指标综合指数: 0 0 1 0 q p q p 公式中: q代表数量指标,p代表质量指标 下标 1 代表报告期,0 代表基期 质量指标综合指数: 1 0 1 1 q p q p 当所研究的指数化指标为数量指标时,称为数 量指标综合指数,其同度量因素为基期质量指标。 当所研究的指数化指标为质量指标时,称为质量 指标综合指数,其同度量因素为报告期数量指标。 即:

(二) 综合指数分析方法 1、数量指标综合指数分析 相对数分析: 9o Po 公式分子与分母的比值反映了所研究的数 量指标报告期比基期相对综合变动程度。 绝对数分析: ∑9P。-∑qoP0 公式分子减分母的差额,反映了由于所分析的数 量指标的变动,使价值量指标增加或减少的数额
(二)综合指数分析方法 0 0 1 0 q p q p 公式分子与分母的比值反映了所研究的数 量指标报告期比基期相对综合变动程度。 q1 p0 −q0 p0 公式分子减分母的差额,反映了由于所分析的数 量指标的变动,使价值量指标增加或减少的数额。 1、数量指标综合指数分析 相对数分析: 绝对数分析: