
《高等数学II》课程教学大纲 一、课程基本信息 课程中文名称高等数学 课程英文名称Higher MathematicsⅡ 课程编号 106121002 适用专业 物理学(师范)专业全日制本利 学生 课程模块 专业课程-学科基础 课程类别 专业必修 开课单位物理与信息工程系 教研室 理论物理 开课学期第2学期(一年级第二学期)考核方式 笔试(闭卷) 学时 48 理论学时 48 实验学时 0 学分 3 先修课程高等数学1 教材选用同济大学数学系编.《高等数学》下册.高等教有出版社,2007(第六版) 二、课程简介 高等数学IⅡ是高等学校物理专业学生一门必修的重要基础课,通过本课程的学习要使学生获得: 1)向量代数和空间解析几何: 2》多元函数徽积分学: 3)重积分: 4)曲线积分与曲面积分: 5)无穷级数: 五个方面的基本概念、基本理论和基本运算技能。 高等数学Ⅱ在传授以上5方面的基本概念、基本理论和基本运算技能的同时,要通过各个教学 环节逐步培养学生具有抽象概括问题的能力、逻辑推理能力和自学能力,还要特别注意培养学生具 有比较熟练的运算能力和综合运用所学知识去分析问题和解决实际问题的能力,从而使学生具有一 定的数学素养
14 《高等数学 II》课程教学大纲 一、课程基本信息 课程中文名称 高等数学 II 课程英文名称 Higher Mathematics II 课程编号 106121002 适用专业 物理学(师范)专业全日制本科 学生 课程模块 专业课程-学科基础 课程类别 专业必修 开课单位 物理与信息工程系 教 研 室 理论物理 开课学期 第 2 学期(一年级第二学期) 考核方式 笔试(闭卷) 学 时 48 理论学时 48 实验学时 0 学 分 3 先修课程 高等数学 I 教材选用 同济大学数学系编.《高等数学》下册. 高等教育出版社,2007(第六版). 二、课程简介 高等数学 II 是高等学校物理专业学生一门必修的重要基础课,通过本课程的学习要使学生获得: 1)向量代数和空间解析几何; 2)多元函数微积分学; 3)重积分; 4)曲线积分与曲面积分; 5) 无穷级数; 五个方面的基本概念、基本理论和基本运算技能。 高等数学 II 在传授以上 5 方面的基本概念、基本理论和基本运算技能的同时,要通过各个教学 环节逐步培养学生具有抽象概括问题的能力、逻辑推理能力和自学能力,还要特别注意培养学生具 有比较熟练的运算能力和综合运用所学知识去分析问题和解决实际问题的能力,从而使学生具有一 定的数学素养

三、课程目标 课程目标 对应的专业培养目标 掌提学习物理学所需的高等数学基础知识和 理解向量代数和空间解析几何: 基本计算技能 2.掌握多元函数微积分学、重积分、曲线积分 曲面积分、无穷级数等内容的概念、计算与应用。 四、课程重难点 课程重点 课程难点 向量代数和空间解析几何 1.空间曲面的绘制 多元函数微积分学 2.复合函数和隐函数的偏导数 3.重积分 3.三重积分 4.第二类曲线积分与第二类曲面积分 5.无穷级数 4.第二类曲面积分 5.傅里叶级数 五、教学方式与方法 教学方式与方法学时占比教学方式与方法学时占比教学方式与方法学时占比 1.讲授法教学 2.体验学习 36 75% 25% (习题课) 六、考核形式及成绩评定 评价方式 占比 评价方式 占比评价方式 占比 平时考核1.作业撰写 5%2.期中测试 20%3.出勤率 5% 期末考核笔试(闭卷) 70% 成绩评定 平时成绩(10%)+期中成绩(20%)+期末成绩(70%) 七、教学内容及学时分配 课次学时章目名称 教学内容及教学目标 教学方式 评价方式 向量及其线性计算: 第八章向量代数 和空间解析几何,向量的概念、模、单位向量、正交分 讲授 筑一节 解、方向余弦(掌握) 第二节至第三节掌握:数量积、向量积、混合积,旋 讲授(2) 3 曲面方程 转曲面,柱面,二次曲面: 习题课(1)
15 三、课程目标 课程目标 对应的专业培养目标 掌握学习物理学所需的高等数学基础知识和 基本计算技能 1.理解向量代数和空间解析几何; 2.掌握多元函数微积分学、重积分、曲线积分与 曲面积分、无穷级数等内容的概念、计算与应用。 四、课程重难点 课程重点 课程难点 1. 向量代数和空间解析几何 2. 多元函数微积分学 3. 重积分 4. 第二类曲线积分与第二类曲面积分 5. 无穷级数 1. 空间曲面的绘制 2.复合函数和隐函数的偏导数 3. 三重积分 4. 第二类曲面积分 5. 傅里叶级数 五、教学方式与方法 教学方式与方法 学时 占比 教学方式与方法 学时 占比 教学方式与方法 学时 占比 1.讲授法教学 36 75% 2.体验学习 (习题课) 12 25% 六、考核形式及成绩评定。 评价方式 占比 评价方式 占比 评价方式 占比 平时考核 1. 作业撰写 5 % 2. 期中测试 20 % 3. 出勤率 5% 期末考核 笔试(闭卷) 70% 成绩评定 平时成绩(10%)+期中成绩(20 %)+期末成绩(70%) 七、教学内容及学时分配 课次 学时 章目名称 教学内容及教学目标 教学方式 评价方式 1 3 第八章向量代数 和空间解析几何, 第一节 向量及其线性计算: 向量的概念、模、单位向量、正交分 解、方向余弦(掌握) 讲授 2 3 第二节至第三节 曲面方程 掌握:数量积、向量积、混合积,旋 转曲面,柱面,二次曲面; 讲授(2) 习题课(1)
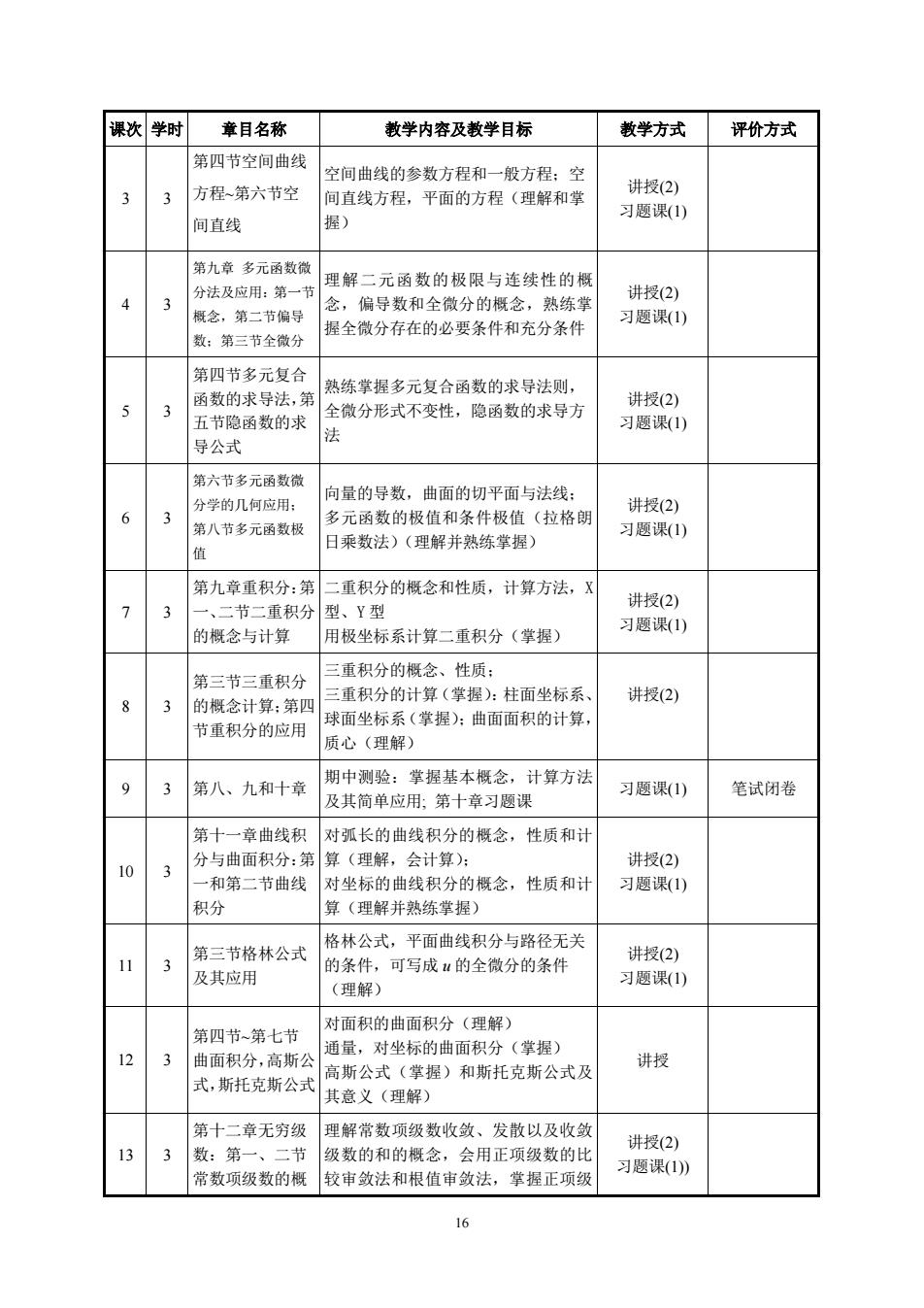
课次学时 章目名称 教学内容及教学目标 教学方式 评价方式 第四节空间曲线 空间曲线的参数方程和一般方程: 方程第六节空 间直线方程,平面的方程(理解和学 讲授(2) 间省线 握) 习题课(1) 第九.煮多元函数潜 理解二元函数的极限与连续性的概 公法马应用。教士 3 概念,第二节偏号 念,偏导数和全微分的概念,熟练掌 讲授2) 全微分存在的必要条件和充分条件 习题课(1) 数:第三节全微分 第四节多元复合 函数的求导法,第 熟练掌握多元复合函数的求导法则, 讲授(2) 3 五节隐函数的求 全微分形式不变性,隐函数的求导方 习题课(1) 导公式 第六节多元函数微 向量的导数,曲面的切平面与法线 3 多元函数的极 讲授(2) 1和条件极但 (拉格朗 习题课(1) 日乘数法)(理解并熟练掌握) 第九章重积分:第 二重积分的概念和性质,计算方法,X 讲授(2) 、二节二重积分型、Y型 习题课1 的概念与计算 用极坐标系计算二重积分(掌握) 三重积分的概念、性质: 的概念计算:第 :重积分的 十算(掌握):柱面坐标系 井授(2) 球面坐标系(掌握):曲面面积的计算 节重积分的应用 质心(理解) 第八、九和十意 期中测验:掌握基本概念,计算方法 3 习题课(1) 笔试闭卷 及其简单应用:第十章习题课 第十一意曲线积 对弧长的曲线积分的概念,性质和计 3 分与曲面积分:第算(理解,会计算): 讲授(2) 和第 节曲线 对坐标的曲线积分的概念,性质和计 习题课(1) 积分 算(理解并熟练掌握) 格林公式,平面曲线积分与路径无关 第三节格林公式 讲授2) 3 及比应用 的条件,可写成“的全微分的条件 (理解) 习题课(1) 对面积的曲面积分(理解) 第四节、第十节 12 3 曲面积分 高斯 通量,对坐标的曲面积分(掌握) 高斯公式 (掌握)和斯托克斯公式 讲授 式,斯托克斯公 其意义(理解) 第十二章无穷级 理解常数项级数收敛、发散以及收敛 3 数:第一、二节级数的和的概念,会用正项级数的比 讲授(2) 常数项级数的概 习题课(1)》 较审敛法和根值审敛法,堂握正顶级
16 课次 学时 章目名称 教学内容及教学目标 教学方式 评价方式 3 3 第四节空间曲线 方程~第六节空 间直线 空间曲线的参数方程和一般方程;空 间直线方程,平面的方程(理解和掌 握) 讲授(2) 习题课(1) 4 3 第九章 多元函数微 分法及应用:第一节 概念,第二节偏导 数;第三节全微分 理解二元函数的极限与连续性的概 念,偏导数和全微分的概念,熟练掌 握全微分存在的必要条件和充分条件 讲授(2) 习题课(1) 5 3 第四节多元复合 函数的求导法,第 五节隐函数的求 导公式 熟练掌握多元复合函数的求导法则, 全微分形式不变性,隐函数的求导方 法 讲授(2) 习题课(1) 6 3 第六节多元函数微 分学的几何应用; 第八节多元函数极 值 向量的导数,曲面的切平面与法线; 多元函数的极值和条件极值(拉格朗 日乘数法)(理解并熟练掌握) 讲授(2) 习题课(1) 7 3 第九章重积分:第 一、二节二重积分 的概念与计算 二重积分的概念和性质,计算方法,X 型、Y 型 用极坐标系计算二重积分(掌握) 讲授(2) 习题课(1) 8 3 第三节三重积分 的概念计算;第四 节重积分的应用 三重积分的概念、性质; 三重积分的计算(掌握):柱面坐标系、 球面坐标系(掌握);曲面面积的计算, 质心(理解) 讲授(2) 9 3 第八、九和十章 期中测验:掌握基本概念,计算方法 及其简单应用; 第十章习题课 习题课(1) 笔试闭卷 10 3 第十一章曲线积 分与曲面积分:第 一和第二节曲线 积分 对弧长的曲线积分的概念,性质和计 算(理解,会计算); 对坐标的曲线积分的概念,性质和计 算(理解并熟练掌握) 讲授(2) 习题课(1) 11 3 第三节格林公式 及其应用 格林公式,平面曲线积分与路径无关 的条件,可写成 u 的全微分的条件 (理解) 讲授(2) 习题课(1) 12 3 第四节~第七节 曲面积分,高斯公 式,斯托克斯公式 对面积的曲面积分(理解) 通量,对坐标的曲面积分(掌握) 高斯公式(掌握)和斯托克斯公式及 其意义(理解) 讲授 13 3 第十二章无穷级 数:第一、二节 常数项级数的概 理解常数项级数收敛、发散以及收敛 级数的和的概念,会用正项级数的比 较审敛法和根值审敛法,掌握正项级 讲授(2) 习题课(1))
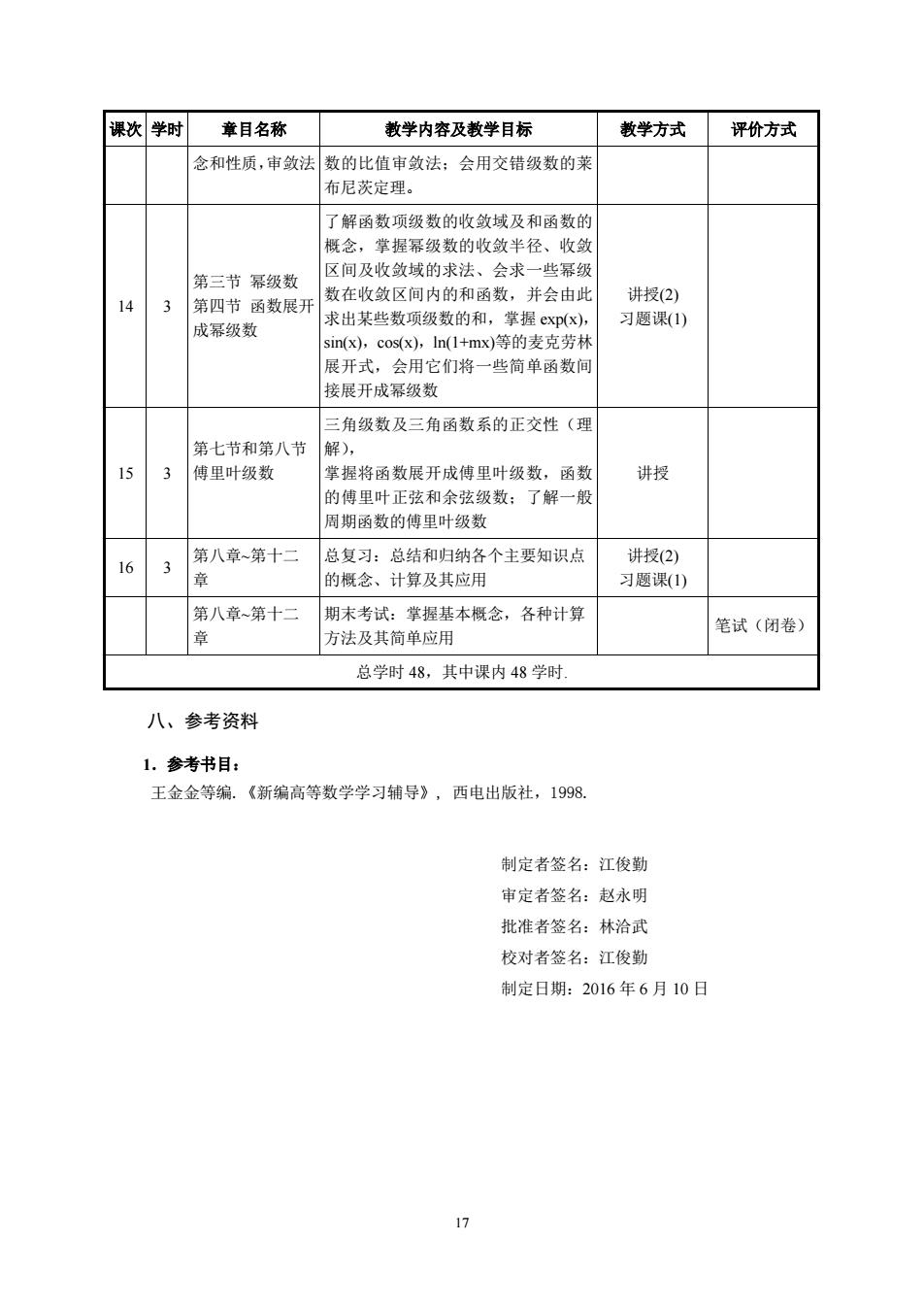
课次学时 章目名称 教学内容及教学目标 教学方式 评价方式 念和性质,审敛法 数的比值审敛法:会用交错级数的菜 布尼茨定理。 了解函数项级数的收敛域及和函数的 概念,掌握幂级数的收敛半径、收敛 风间及收敛域的求法、会求一些磊级 第三节系级勒 14 3 第四节函数展) 数在收敛区间内的和函数,并会由此 讲授(2) 求出某些数项级数的和,掌握xp(x) 习题课(1) 成幂级数 sin(x),cosx,ln(I+mx)等的麦克劳林 展开式,会用它们将一些简单函数间 接展开成幂级数 三角级数及三角函数系的正交性(理 第七节和第八节 15 3 傅里叶级数 握将函数展开成傅里叶级数, 函数 讲授 的傅里叶正弦和余弦级数:了解一般 周期函数的傅里叶级数 6 3 第八章第十二 总复习:总结和归纳各个主要知识点 讲授(2) 的概念、计算及其应用 习题课(1) 第八章第十一 期末考试:掌握基本概念,各种计算 章 方法及其简单应用 笔试(闭卷) 总学时48,其中课内48学时 八、参考资料 1.参考书目: 王金金等编。《新编高等数学学习辅导》,西电出版社,1998, 制定者签名:江俊勤 审定者签名:赵水明 批准者签名:林治武 校对者签名:江俊勤 制定日期:2016年6月10日
17 课次 学时 章目名称 教学内容及教学目标 教学方式 评价方式 念和性质,审敛法 数的比值审敛法;会用交错级数的莱 布尼茨定理。 14 3 第三节 幂级数 第四节 函数展开 成幂级数 了解函数项级数的收敛域及和函数的 概念,掌握幂级数的收敛半径、收敛 区间及收敛域的求法、会求一些幂级 数在收敛区间内的和函数,并会由此 求出某些数项级数的和,掌握 exp(x), sin(x),cos(x),ln(1+mx)等的麦克劳林 展开式,会用它们将一些简单函数间 接展开成幂级数 讲授(2) 习题课(1) 15 3 第七节和第八节 傅里叶级数 三角级数及三角函数系的正交性(理 解), 掌握将函数展开成傅里叶级数,函数 的傅里叶正弦和余弦级数;了解一般 周期函数的傅里叶级数 讲授 16 3 第八章~第十二 章 总复习:总结和归纳各个主要知识点 的概念、计算及其应用 讲授(2) 习题课(1) 第八章~第十二 章 期末考试:掌握基本概念,各种计算 方法及其简单应用 笔试(闭卷) 总学时 48,其中课内 48 学时. 八、参考资料 1.参考书目: 王金金等编.《新编高等数学学习辅导》, 西电出版社,1998. 制定者签名:江俊勤 审定者签名:赵永明 批准者签名:林洽武 校对者签名:江俊勤 制定日期:2016 年 6 月 10 日
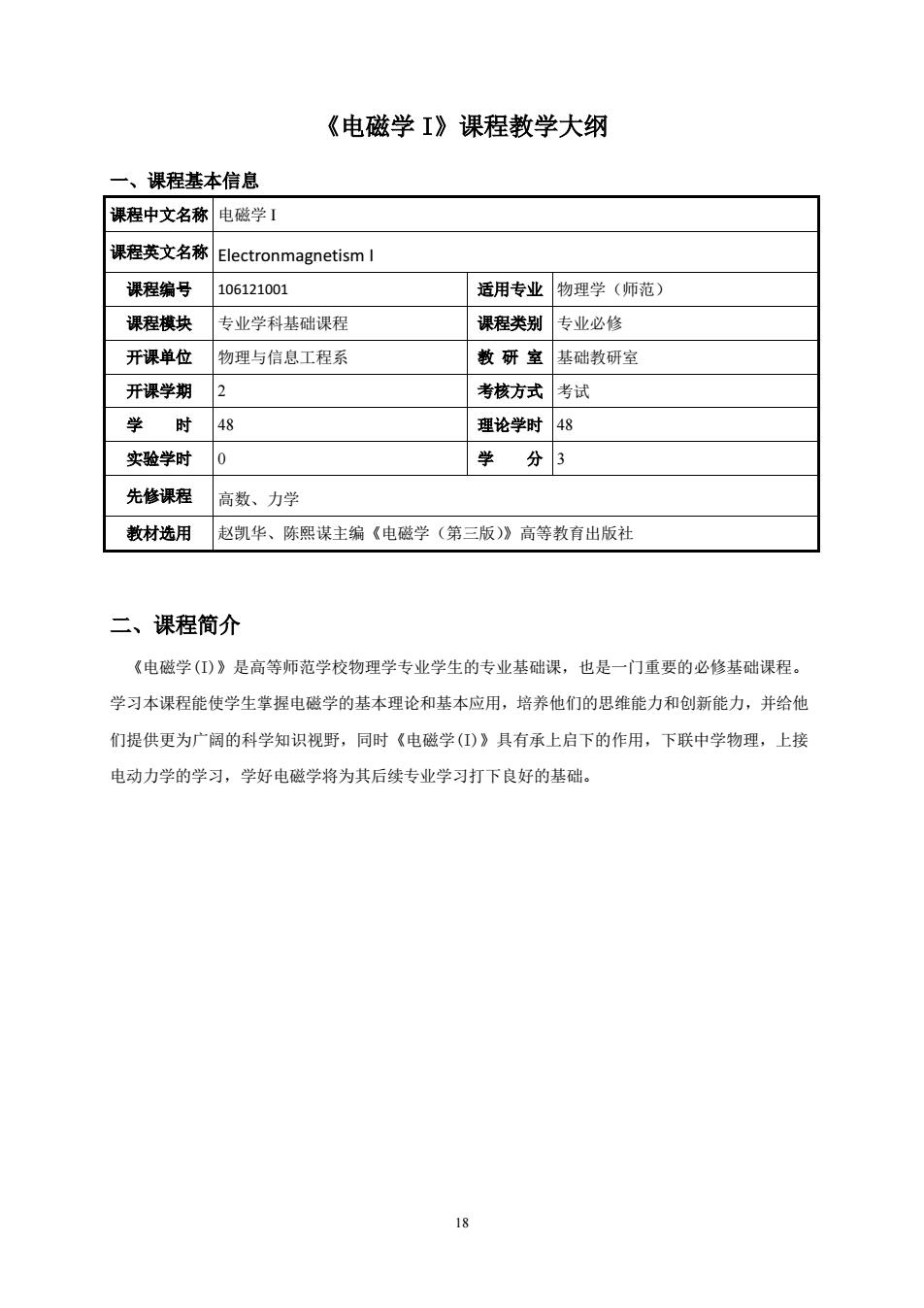
《电磁学I》课程教学大纲 一、课程基本信息 课程中文名称电磁学】 课程英文名称ElectronmagnetismI 课程编号106121001 适用专业物理学(师范) 课程模块 专业学科基础课程 课程类别专业必修 开课单位物理与信息工程系 教研室基础教研室 开课学期 2 考核方式考试 学时48 理论学时48 实验学时0 学分3 先修课程高数、力学 教材选用赵凯华、陈熙谋主编《电磁学(第三版)》高等教有出版社 二、课程简介 《电磁学(①)》是高等师范学校物理学专业学生的专业基础课,也是一门重要的必修基础课程。 学习本课程能使学生掌握电磁学的基本理论和基本应用,培养他们的思维能力和创新能力,并给他 们提供更为广阔的科学知识视野,同时《电磁学(D》具有承上启下的作用,下联中学物理,上接 电动力学的学习,学好电磁学将为其后续专业学习打下良好的基础
18 《电磁学 I》课程教学大纲 一、课程基本信息 课程中文名称 电磁学 I 课程英文名称 Electronmagnetism I 课程编号 106121001 适用专业 物理学(师范) 课程模块 专业学科基础课程 课程类别 专业必修 开课单位 物理与信息工程系 教 研 室 基础教研室 开课学期 2 考核方式 考试 学 时 48 理论学时 48 实验学时 0 学 分 3 先修课程 高数、力学 教材选用 赵凯华、陈熙谋主编《电磁学(第三版)》高等教育出版社 二、课程简介 《电磁学(I)》是高等师范学校物理学专业学生的专业基础课,也是一门重要的必修基础课程。 学习本课程能使学生掌握电磁学的基本理论和基本应用,培养他们的思维能力和创新能力,并给他 们提供更为广阔的科学知识视野,同时《电磁学(I)》具有承上启下的作用,下联中学物理,上接 电动力学的学习,学好电磁学将为其后续专业学习打下良好的基础