
第5期 李航,等:基于Spark的多标签超网络集成学习 ·629 12)每条样本生成e条超边 区计算获胜节点,并更新优胜邻域中的输出单元, 13)end flatmap.cache 然后将各个分区的值利用reduce算子进行合并,并 14)Ho=Hii .map 更新优胜邻域,达到终止条件得到最终输出层。其 15)对超边进行1,次替代 中,计算邻域函数选取高斯函数,距离仍然选取欧 16)end map.cache 氏距离,WBro为SOM初始化输出层W的广播变量 17)for t+l to t do 在6)~12)中完成了一次迭代计算,旷为每次迭代 18)HBro broadcast(H) 利用每个分区样本更新后输出层,W旷:为分区合并的 19)Himp=Tky.map 输出层。 20)对样本利用H-'Bro中超边集合预测 训练集 测试集 21)end map.flatmap 22)对超边进行梯度计算 自组织神经网络 <输出层权重 23)end flatmap.reduceByKey(合并梯度值) 选择性集成 24)H'H.leftjoin(H) 训练簇1 训练簇2 训练簇c 获得s个 领域簇 25).map 26)利用合并后梯度值更新超边权重 获得s个对应 SI-MLHN SI-MLHN SI-MLHN 27)end map 局部超网络 28)end for 构成新的 超网路 29)H=H 30)return H 输出 训练过程测试过程 T为训练集经过分布式并行归一化处理后的 结果:broadcast操作可以保存只读变量,并保在每个 图2SEI-MLHN流程图 节点内存中;TBo为归一化后样本广播变量; Fig.2 Flow chart of SEI-MLHN T,Bo为样本与其k近邻的键值对T,的广播变量: 算法3S-S0M Hm为超边初始化集合;H为超边替代后集合;H 输入训练集T={(x.yn)}(1≤n≤N),类 为超边演化学习后集合。 簇个数c,学习率n,迭代次数t; 2.3 Spark下集成多标签超网络(SEI-MLHN)】 输出类簇T1,T,…,T。 SI-MLHN为MLHN的Spark平台下分布式并行 1)T =T.map 改进方法,大幅缩短了训练时间,但是其时间复杂 2)每条样本进行归一化 度仍然随着样本数量的增加呈平方级增长,仍然无 3)end map.cache 法很好适应大样本数据。故本文利用选择性集成, 4)W=初始化输出层(随机抽取c个样本) 一方面降低时间复杂度,另一方面提高算法性能, 5)WBro =broadcast(W) 提出了Spark下集成多标签超网络,记作SEL- 6)for t+1 to ti MLHN。SEI-MLHN首先将训练集进行分簇,并分别 7)for each T的分区do 用SI-MLHN算法演化学习多个局部多标签超网络。 8)for each分区内样本do 对于未知样本,首先获得近邻簇,然后利用局部超 9)利用输出层计算获胜节点 网络选择性集成对测试样本进行预测,SEI-MLHN 10)更新优胜邻域中的值为W 的流程见图2。 11)end for 为了对训练样本进行分簇,本文选择了基于神 12)end for 经网络的无监督聚类方法自组织神经网络 13)更新优胜邻域 (SOM)[。SOM对类簇初始化不敏感,并且可以 l4)W=利用reduce合并各分区W 很好地发现数据之间的结构关系,为了让其适应大 15)end for 规模数据处理将其进行了Spark下并行化扩展,记 16)T1,T,…,T。'=Tm,计算获胜节点(W) 为S-S0M。算法3为算法伪代码,首先利用每个分 17)return T,T,…,T
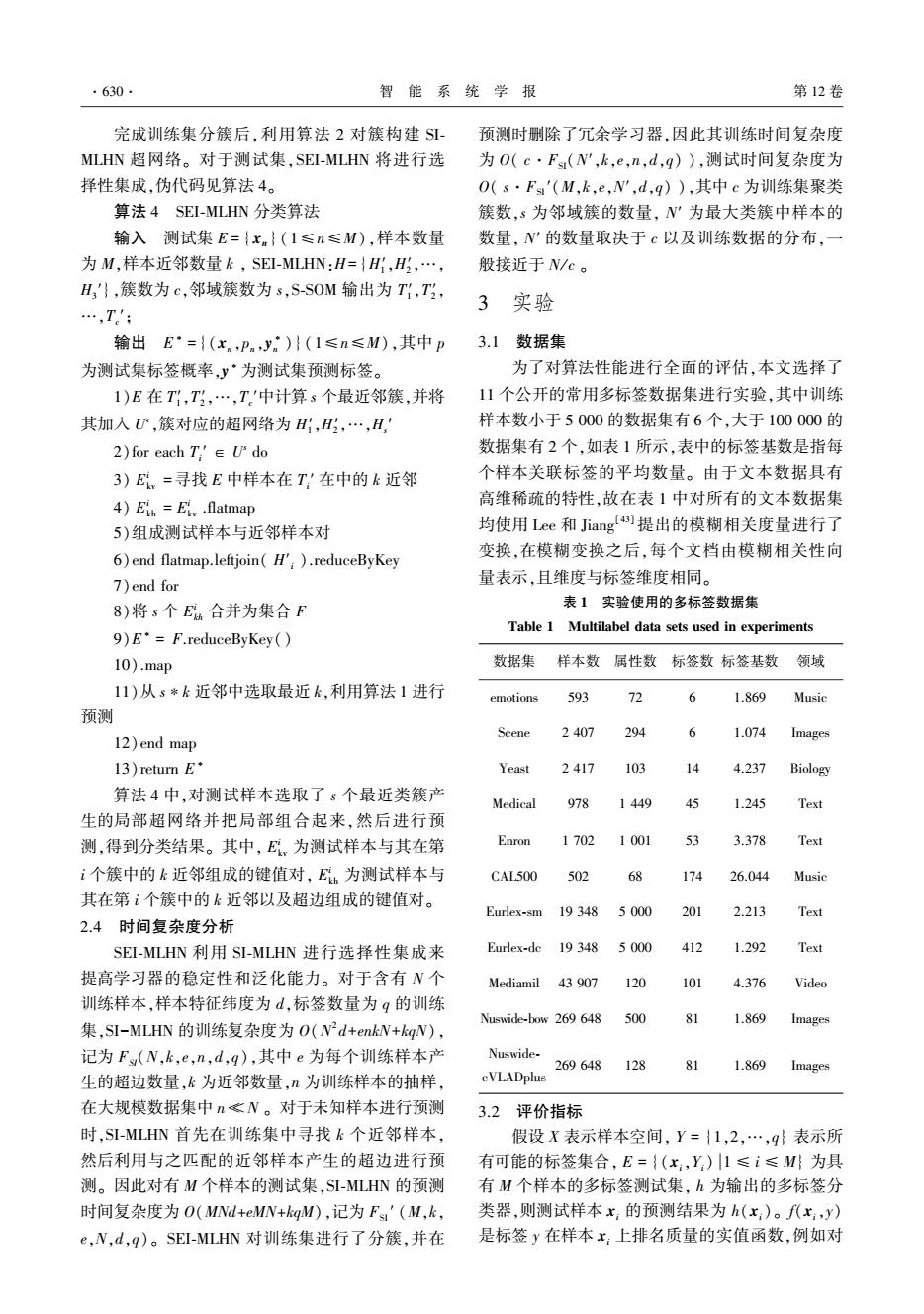
12)每条样本生成 e 条超边 13)end flatmap.cache 14) H 0 re = Hini .map 15)对超边进行 t r次替代 16)end map.cache 17)for t←1 to t d do 18) H t-1 re Bro = broadcast( H t-1 re ) 19)Htmp = Tkv .map 20)对样本利用 H t-1 re Bro 中超边集合预测 21)end map.flatmap 22)对超边进行梯度计算 23)end flatmap.reduceByKey(合并梯度值) 24) H t re = H t-1 re .leftjoin(Htmp ) 25).map 26)利用合并后梯度值更新超边权重 27)end map 28)end for 29)H=H t re 30)return H Tnor 为训练集经过分布式并行归一化处理后的 结果;broadcast 操作可以保存只读变量,并保在每个 节点内存中; TnorBro 为归一化后样本广播变量; TkvBro 为样本与其 k 近邻的键值对 Tkv 的广播变量; Hini为超边初始化集合; H 0 re 为超边替代后集合; H t re 为超边演化学习后集合。 2.3 Spark 下集成多标签超网络(SEI⁃MLHN) SI⁃MLHN 为 MLHN 的 Spark 平台下分布式并行 改进方法,大幅缩短了训练时间,但是其时间复杂 度仍然随着样本数量的增加呈平方级增长,仍然无 法很好适应大样本数据。 故本文利用选择性集成, 一方面降低时间复杂度,另一方面提高算法性能, 提出 了 Spark 下 集 成 多 标 签 超 网 络, 记 作 SEI⁃ MLHN。 SEI⁃MLHN 首先将训练集进行分簇,并分别 用 SI⁃MLHN 算法演化学习多个局部多标签超网络。 对于未知样本,首先获得近邻簇,然后利用局部超 网络选择性集成对测试样本进行预测,SEI⁃MLHN 的流程见图 2。 为了对训练样本进行分簇,本文选择了基于神 经网 络 的 无 监 督 聚 类 方 法 自 组 织 神 经 网 络 (SOM) [42] 。 SOM 对类簇初始化不敏感,并且可以 很好地发现数据之间的结构关系,为了让其适应大 规模数据处理将其进行了 Spark 下并行化扩展,记 为 S⁃SOM。 算法 3 为算法伪代码,首先利用每个分 区计算获胜节点,并更新优胜邻域中的输出单元, 然后将各个分区的值利用 reduce 算子进行合并,并 更新优胜邻域,达到终止条件得到最终输出层。 其 中,计算邻域函数选取高斯函数,距离仍然选取欧 氏距离, WBro 为 SOM 初始化输出层 W 的广播变量 在 6) ~12)中完成了一次迭代计算,W t c 为每次迭代 利用每个分区样本更新后输出层,W t r 为分区合并的 输出层。 图 2 SEI⁃MLHN 流程图 Fig.2 Flow chart of SEI⁃MLHN 算法 3 S⁃SOM 输入 训练集 T = {(xn ,yn )}(1 ≤ n ≤ N) ,类 簇个数 c ,学习率 η,迭代次数 t i; 输出 类簇 T1 ′,T2 ′,…,Ts ′。 1) Tnor = T .map 2)每条样本进行归一化 3)end map.cache 4) W =初始化输出层(随机抽取 c 个样本) 5) WBro = broadcast( W ) 6)for t←1 to t i 7)for each Tnor的分区 do 8)for each 分区内样本 do 9)利用输出层计算获胜节点 10)更新优胜邻域中的值为 W t c 11)end for 12)end for 13)更新优胜邻域 14)W t r =利用 reduce 合并各分区 W t c 15)end for 16)T1 ′,T2 ′,…,Tp ′ = Tnor,计算获胜节点(W t r) 17)return T1 ′,T2 ′,…,Ts ′ 第 5 期 李航,等:基于 Spark 的多标签超网络集成学习 ·629·
·630 智能系统学报 第12卷 完成训练集分簇后,利用算法2对簇构建S- 预测时删除了冗余学习器,因此其训练时间复杂度 MLHN超网络。对于测试集,SEI-MLHN将进行选 为O(c·Fs(N',k,e,n,d,q)),测试时间复杂度为 择性集成,伪代码见算法4。 O(s·Fs'(M,k,e,N',d,q)),其中c为训练集聚类 算法4SEI-MLHN分类算法 簇数,s为邻域簇的数量,N'为最大类簇中样本的 输入测试集E={xn}(1≤n≤M),样本数量 数量,N'的数量取决于c以及训练数据的分布,一 为M,样本近邻数量k,SEI-MLHN:H={H,H,…, 般接近于N/c。 H'},簇数为c,邻域簇数为s,S-SOM输出为T1,T, 3实验 …,T' 输出E·={(x.,Pn,y)}(1≤n≤M),其中p 3.1数据集 为测试集标签概率,y·为测试集预测标签。 为了对算法性能进行全面的评估,本文选择了 1)E在T1,T,…,T'中计算s个最近邻簇,并将 11个公开的常用多标签数据集进行实验,其中训练 其加入心,簇对应的超网络为H,H,…,H, 样本数小于5000的数据集有6个,大于100000的 2)for each T'∈Udo 数据集有2个,如表1所示,表中的标签基数是指每 3)E,=寻找E中样本在T,'在中的k近邻 个样本关联标签的平均数量。由于文本数据具有 4)Eih Eiy .flatmap 高维稀疏的特性,故在表1中对所有的文本数据集 5)组成测试样本与近邻样本对 均使用Lee和Jiang)提出的模糊相关度量进行了 6)end flatmap.leftjoin(H').reduceByKey 变换,在模糊变换之后,每个文档由模糊相关性向 7)end for 量表示,且维度与标签维度相同。 8)将s个E合并为集合F 表1实验使用的多标签数据集 Table 1 Multilabel data sets used in experiments 9)E'=F.reduceByKey() 10).map 数据集 样本数属性数标签数标签基数领域 11)从s*k近邻中选取最近k,利用算法1进行 emotions 593 12 6 1.869 Music 预测 Scene 2407 294 6 1.074 Images 12)end map l3)return E· Yeast 2417 1)3 14 4.237 Biology 算法4中,对测试样本选取了s个最近类簇产 Medical 978 1449 49 1.245 Text 生的局部超网络并把局部组合起来,然后进行预 测,得到分类结果。其中,E。为测试样本与其在第 Enron 1702 3.378 Text i个簇中的k近邻组成的键值对,E为测试样本与 CAL500 502 26.044 Music 其在第i个簇中的k近邻以及超边组成的键值对。 Eurlex-sm 19348 5000 20 2.213 Text 2.4时间复杂度分析 SEI-MLHN利用SI-MLHN进行选择性集成来 Eurlex-de 19 348 50 42 1.292 Text 提高学习器的稳定性和泛化能力。对于含有N个 Mediamil 43 907 120 101 4.376 Video 训练样本,样本特征纬度为d,标签数量为q的训练 Nuswide-bow 269 648 500 6 1.869 Images 集,SI-MLHN的训练复杂度为O(N2d+enkW+kgN), 记为F(N,k,e,n,d,g),其中e为每个训练样本产 Nuswide- 269648 128 81 1.869 Images 生的超边数量,k为近邻数量,n为训练样本的抽样, cVLADplus 在大规模数据集中n客N。对于未知样本进行预测 3.2评价指标 时,SI-MLHN首先在训练集中寻找k个近邻样本, 假设X表示样本空间,Y={1,2,…,9}表示所 然后利用与之匹配的近邻样本产生的超边进行预 有可能的标签集合,E={(x:,Y)1≤i≤M为具 测。因此对有M个样本的测试集,SI-MLHN的预测 有M个样本的多标签测试集,h为输出的多标签分 时间复杂度为O(MNd+eMN+kgM),记为Fs'(M,k, 类器,则测试样本x,的预测结果为h(x:)。f(x,y) e,N,d,q)。SEI-MLHN对训练集进行了分簇,并在 是标签y在样本x:上排名质量的实值函数,例如对
完成训练集分簇后,利用算法 2 对簇构建 SI⁃ MLHN 超网络。 对于测试集,SEI⁃MLHN 将进行选 择性集成,伪代码见算法 4。 算法 4 SEI⁃MLHN 分类算法 输入 测试集 E = { xn } (1≤n≤M),样本数量 为 M,样本近邻数量 k , SEI⁃MLHN:H= {H1 ′,H2 ′,…, H3 ′},簇数为 c,邻域簇数为 s,S⁃SOM 输出为 T1 ′,T2 ′, …,Tc ′; 输出 E ∗ = {(xn ,pn ,y ∗ n )} (1≤n≤M),其中 p 为测试集标签概率,y ∗为测试集预测标签。 1)E 在 T1 ′,T2 ′,…,Tc ′中计算 s 个最近邻簇,并将 其加入 U s ,簇对应的超网络为 H1 ′,H2 ′,…,Hs ′ 2)for each Ti ′ ∈ U s do 3) E i kv =寻找 E 中样本在 Ti ′ 在中的 k 近邻 4) E i kh = E i kv .flatmap 5)组成测试样本与近邻样本对 6)end flatmap.leftjoin( H′i ).reduceByKey 7)end for 8)将 s 个 E i kh 合并为集合 F 9)E ∗ = F.reduceByKey() 10).map 11)从 s∗k 近邻中选取最近 k,利用算法 1 进行 预测 12)end map 13)return E ∗ 算法 4 中,对测试样本选取了 s 个最近类簇产 生的局部超网络并把局部组合起来,然后进行预 测,得到分类结果。 其中, E i kv 为测试样本与其在第 i 个簇中的 k 近邻组成的键值对, E i kh 为测试样本与 其在第 i 个簇中的 k 近邻以及超边组成的键值对。 2.4 时间复杂度分析 SEI⁃MLHN 利用 SI⁃MLHN 进行选择性集成来 提高学习器的稳定性和泛化能力。 对于含有 N 个 训练样本,样本特征纬度为 d,标签数量为 q 的训练 集,SI-MLHN 的训练复杂度为 O(N 2 d+enkN+kqN), 记为 FSI(N,k,e,n,d,q),其中 e 为每个训练样本产 生的超边数量,k 为近邻数量,n 为训练样本的抽样, 在大规模数据集中 n ≪ N 。 对于未知样本进行预测 时,SI⁃MLHN 首先在训练集中寻找 k 个近邻样本, 然后利用与之匹配的近邻样本产生的超边进行预 测。 因此对有 M 个样本的测试集,SI⁃MLHN 的预测 时间复杂度为 O(MNd+eMN+kqM),记为 FSI ′ (M,k, e,N,d,q)。 SEI⁃MLHN 对训练集进行了分簇,并在 预测时删除了冗余学习器,因此其训练时间复杂度 为 O( c·FSI(N′,k,e,n,d,q) ),测试时间复杂度为 O( s·FSI ′(M,k,e,N′,d,q) ),其中 c 为训练集聚类 簇数,s 为邻域簇的数量, N′ 为最大类簇中样本的 数量, N′ 的数量取决于 c 以及训练数据的分布,一 般接近于 N/ c 。 3 实验 3.1 数据集 为了对算法性能进行全面的评估,本文选择了 11 个公开的常用多标签数据集进行实验,其中训练 样本数小于 5 000 的数据集有 6 个,大于 100 000 的 数据集有 2 个,如表 1 所示,表中的标签基数是指每 个样本关联标签的平均数量。 由于文本数据具有 高维稀疏的特性,故在表 1 中对所有的文本数据集 均使用 Lee 和 Jiang [43] 提出的模糊相关度量进行了 变换,在模糊变换之后,每个文档由模糊相关性向 量表示,且维度与标签维度相同。 表 1 实验使用的多标签数据集 Table 1 Multilabel data sets used in experiments 数据集 样本数 属性数 标签数 标签基数 领域 emotions 593 72 6 1.869 Music Scene 2 407 294 6 1.074 Images Yeast 2 417 103 14 4.237 Biology Medical 978 1 449 45 1.245 Text Enron 1 702 1 001 53 3.378 Text CAL500 502 68 174 26.044 Music Eurlex⁃sm 19 348 5 000 201 2.213 Text Eurlex⁃dc 19 348 5 000 412 1.292 Text Mediamil 43 907 120 101 4.376 Video Nuswide⁃bow 269 648 500 81 1.869 Images Nuswide⁃ cVLADplus 269 648 128 81 1.869 Images 3.2 评价指标 假设 X 表示样本空间, Y = {1,2,…,q} 表示所 有可能的标签集合, E = {(xi,Yi) 1 ≤ i ≤ M} 为具 有 M 个样本的多标签测试集, h 为输出的多标签分 类器,则测试样本 xi 的预测结果为 h(xi)。 f(xi,y) 是标签 y 在样本 xi 上排名质量的实值函数,例如对 ·630· 智 能 系 统 学 报 第 12 卷