上浒充通大学 2.1.1数制、转换及编码 SHANGHAI JLAO TONG UNIVERSITY ①二进制数转换成士进制数 记住以2为底的指数值,直接写出转换结果!! 权值 2726 25 24 23 22 21 20 2122 8421码 1286432 168 4 2 1 112114 [例1]将二进制数101.12 转换成十进制数 101.12=4+0+1+0.5=5.5
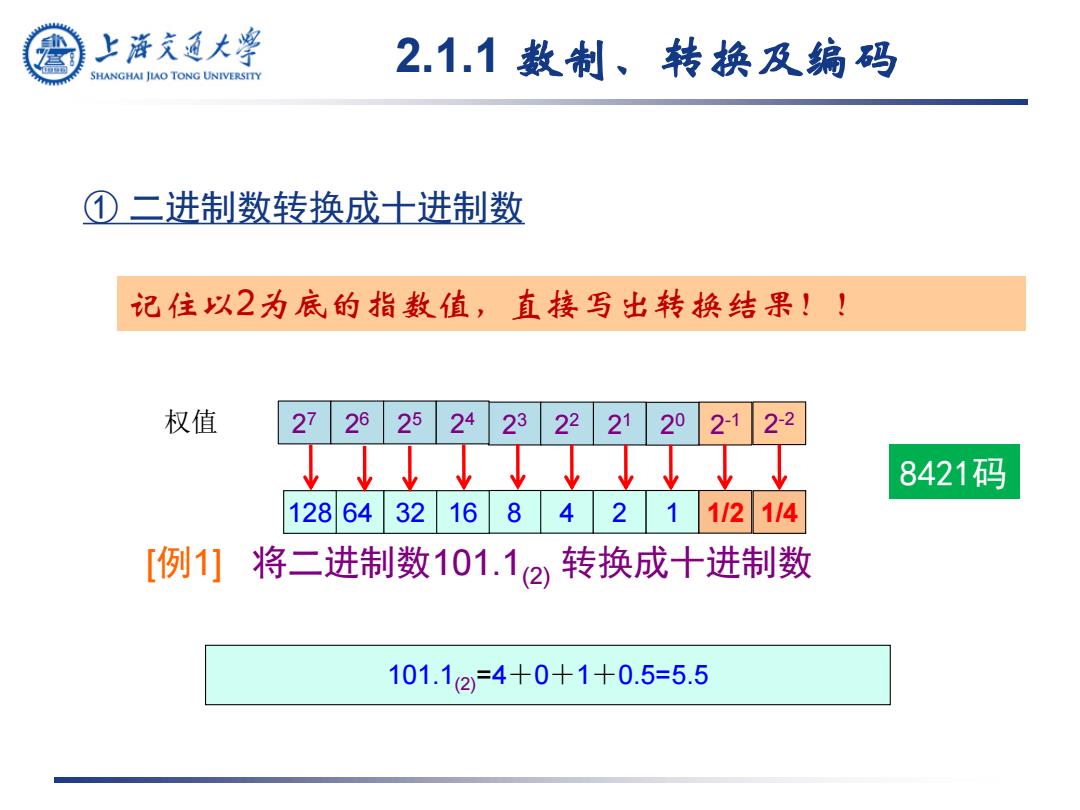
2.1.1 数制、转换及编码 ① 二进制数转换成十进制数 [例1] 将二进制数101.1(2) 转换成十进制数 记住以2为底的指数值,直接写出转换结果!! 101.1(2)=4+0+1+0.5=5.5 8 4 2 1 1/2 2 3 2 2 2 1 2 0 2 权值 -1 128 64 32 16 1/4 2 7 2 6 2 5 2 4 2 -2 8421码
上游充通大学 2.1.1数制、转换及编码 SHANGHAI JLAO TONG UNIVERSITY ②士进制数转换成二进制数 整数部分用除2取余法 0 十进制数有整数和小数两部分,转换时: 2)1.… 高位 整数部分采用除2取余法,小数部分采用乘 2)3...1 2取整法,然后通过小数点将转换后的二进 2)6.......0 制数连接起来即可。 2)13.....1 [例2]将105.62510转换成二进制数 2)26..0 105.62510)=1101001.1012 2)52.....0 2)105.....1 低位 (见右图) 小数部分用乘2取整法 105.62510=64+32+8+1+0.5+0.125 0.625 =1101001.101 X 2 1.250..... 高位 弄清二进制数与十进制数的互换方法,可 X 2 0.500.. 将其推广到其它进制与十进制数的互换, X 2 不同之处是应该考虑具体进制的基数,而 1.000 1 低位 转换算法完全是一样的
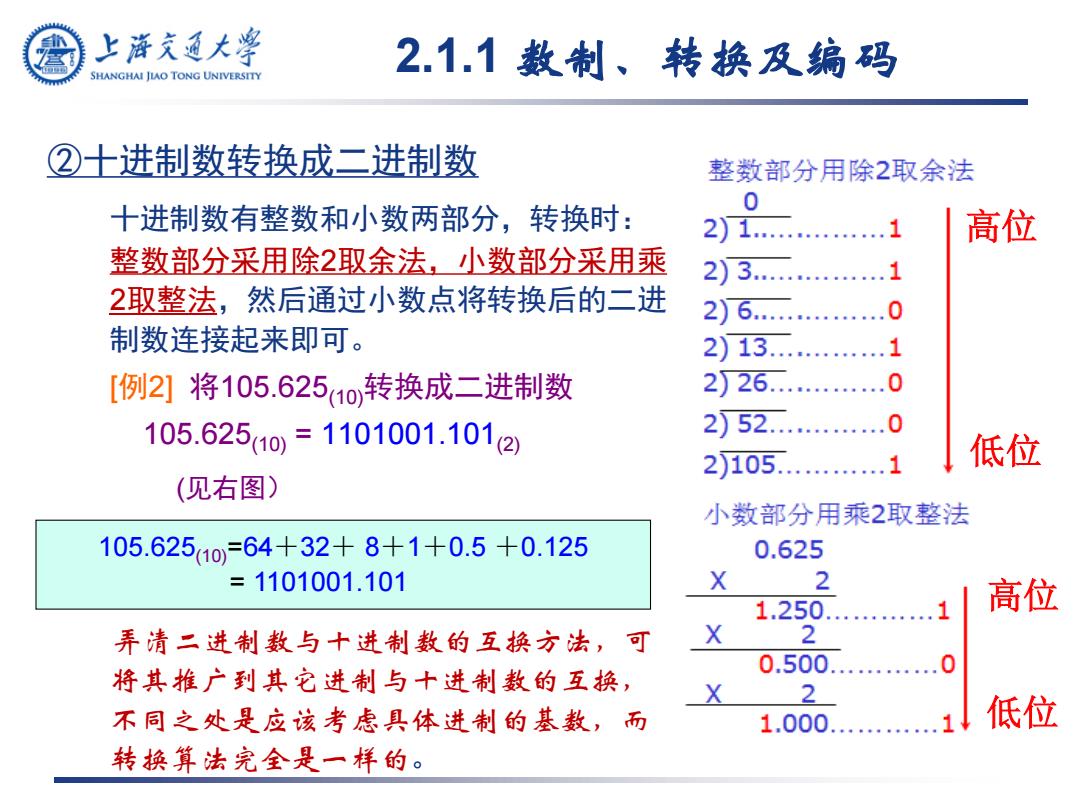
2.1.1 数制、转换及编码 ②十进制数转换成二进制数 十进制数有整数和小数两部分,转换时: 整数部分采用除2取余法,小数部分采用乘 2取整法,然后通过小数点将转换后的二进 制数连接起来即可。 [例2] 将105.625(10)转换成二进制数 105.625(10) = 1101001.101(2) (见右图) 弄清二进制数与十进制数的互换方法,可 将其推广到其它进制与十进制数的互换, 不同之处是应该考虑具体进制的基数,而 转换算法完全是一样的。 低位 高位 高位 低位 105.625(10)=64+32+ 8+1+0.5 +0.125 = 1101001.101

上游充通大学 2.1.1数制、转换及编码 SHANGHAI JLAO TONG UNIVERSITY (2) 二进制数与十六进制数的互换 二进制数与十六进制数之间也存在二进制数与八进制数之间相似的 关系。由于24=16,161=16,即二进制四位数对应于土六进制一位 数。 ①二进制数转换成士六进制数 二进制数转换为十六进制数可概括为“四位并一位”。即以小数点 为基准,整数部分从右至左,小数部分从左至右,每四位一组,不 足四位添0补足。然后将每组的四位二进制数按权展开后相加,得到 一位十六进制数码,再按权的顺序连接起来即得到相应的十六进制 数。 ← [例3]将1011100j001112转换为十六进制数 0101,11000011,10002=5C.38(16 5 C.3 8
2.1.1 数制、转换及编码 (2) 二进制数与十六进制数的互换 二进制数与十六进制数之间也存在二进制数与八进制数之间相似的 关系。由于2 4=16,161=16,即二进制四位数对应于十六进制一位 数。 ①二进制数转换成十六进制数 二进制数转换为十六进制数可概括为“四位并一位”。即以小数点 为基准,整数部分从右至左,小数部分从左至右,每四位一组,不 足四位添0补足。然后将每组的四位二进制数按权展开后相加,得到 一位十六进制数码,再按权的顺序连接起来即得到相应的十六进制 数。 [例3] 将1011100.00111(2)转换为十六进制数 0101,1100.0011,1000(2)=5C.38(16) 5 C . 3 8

上游充通大学 2.1.1数制、转换及编码 SHANGHAI JLAO TONG UNIVERSITY ②十六进制数转换成二进制数 十六进制数转换成二进制数可概括为“一位拆四位”, 即把一位十六进制数写成对应的四位二进制数,然后按 权连接即可。 [例4]将16E.5F(16转换成二进制数 不能略去!! 1 6 E.5 F16 0001,0110,1110.0101,1111 思考题:二进制数和八进制数之间如何相互转换? [倒s1:]将362.478转换成二进制数。 [例s2:]将1011100.001112转换为八进制数
2.1.1 数制、转换及编码 ②十六进制数转换成二进制数 十六进制数转换成二进制数可概括为“一位拆四位”, 即把一位十六进制数写成对应的四位二进制数,然后按 权连接即可。 [例4] 将16E.5F(16)转换成二进制数 1 6 E . 5 F (16)=101101110.01011111(2) 0001,0110,1110.0101,1111 思考题:二进制数和八进制数之间如何相互转换? [例s1:] 将362.47(8)转换成二进制数。 [例s2:] 将1011100.00111(2)转换为八进制数。 000 不能略去!!

上游充通大学 2.1.1数制、转换及编码 SHANGHAI JLAO TONG UNIVERSITY (3)BCD(Binary-Coded Decimal)编码的 数制及转换 二进码十进数 十进 BCD 制数 码 十进制转二进制数有两种方法:整体转换和BCD转换 0000 (即二进制编码的十进制数): 0001 整体转换:基于2为除数,将十进制数作为整体进 0010 行处理(见前节) 3 0011 4 0100 BCD转换:用10种半字节(即4位)的组合分别对应 5 0101 每位十进制数。BCD码是用二进制数表示十进制 6 0110 0~9单个数字的一种方法。具体对应的BCD码见 7 0111 8 1000 右表: 由此可见,1010、1011、1100、1101、 9 1001 1110和1111在BCD数制系统中是不存在的!
2.1.1 数制、转换及编码 (3) BCD(Binary-Coded Decimal)编码的 数制及转换 十进制转二进制数有两种方法:整体转换和BCD转换 (即二进制编码的十进制数): 整体转换:基于2为除数,将十进制数作为整体进 行处理(见前节) BCD转换:用10种半字节(即4位)的组合分别对应 每位十进制数。BCD码是用二进制数表示十进制 0~9单个数字的一种方法。具体对应的BCD码见 右表: 十进 制数 BCD 码 0 0000 1 0001 2 0010 3 0011 4 0100 5 0101 6 0110 7 0111 8 1000 由此可见, 9 1001 1010、1011、1100、1101、 1110和1111在BCD数制系统中是不存在的! 二进码十进数