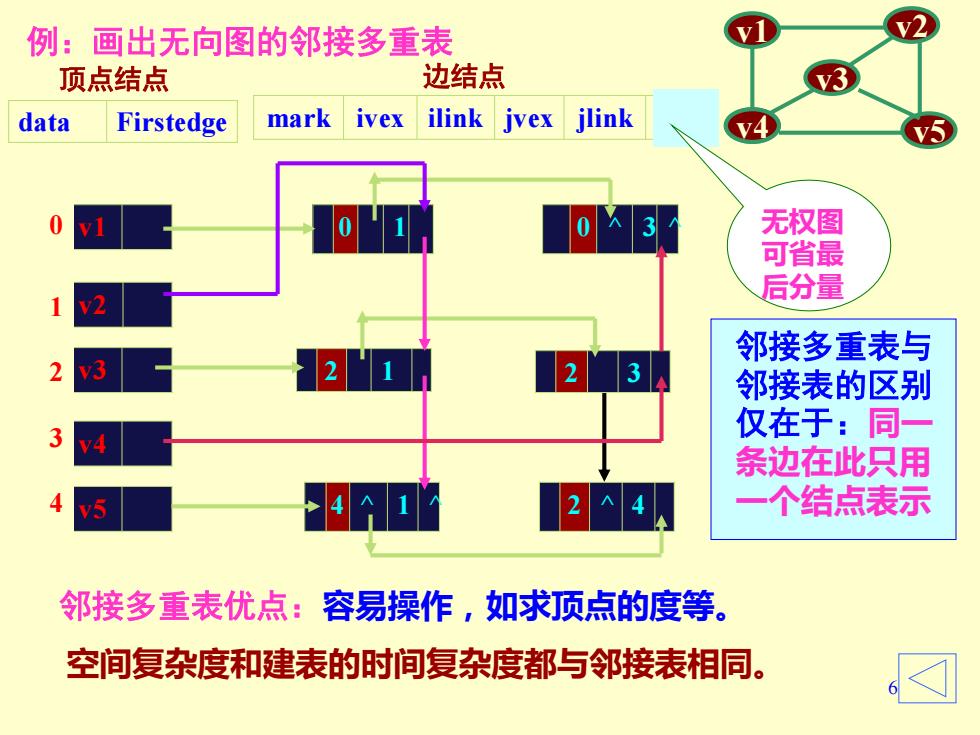
例:画出无向图的邻接多重表 顶点结点 边结点 data Firstedge mark ivex ilink jvex jlink 无权图 可省最 后分量 邻接多重表与 2 邻接表的区别 仅在于:同 条边在此只用 一个结点表示 邻接多重表优点:容易操作,如求顶点的度等。 空间复杂度和建表的时间复杂度都与邻接表相同
6 v1 v2 v3 v4 v5 例:画出无向图的邻接多重表 邻接多重表优点:容易操作,如求顶点的度等。 0 v1 1 v2 2 v3 3 v4 4 v5 0 1 2 3 4 data Firstedge 顶点结点 mark ivex ilink jvex jlink info 边结点 空间复杂度和建表的时间复杂度都与邻接表相同。 0 1 0 ^ 3 ^ 无权图 可省最 后分量 2 1 2 3 4 ^ 1 ^ 2 ^ 4 邻接多重表与 邻接表的区别 仅在于:同一 条边在此只用 一个结点表示

7.3 图的遍历 遍历定义:从已给的连通图中某一顶点出发,沿着一些边,访 遍图中所有的顶点,且使每个顶点仅被访问一次,就叫做 图的遍历,它是图的基本运算。 遍历实质:找每个顶点的邻接点的过程。 图的特点:图中可能存在回路,且图的任一顶点都可能与其它 顶点相通,在访问完某个顶点之后可能会沿着某些边又回 到了曾经访问过的顶点。怎样避免重复访问? 解决思路:可设置一个辅助数组visited[n】,用来标记每个被 访问过的顶点。它的初始状态为0,在图的遍历过程中, 一旦某一个顶点被访问,就立即改visited[为1,防止它 被多次访问。 深度优先搜索 图常用的遍历: 广度优先搜索
7 一、深度优先搜索 二、广度优先搜索 7.3 图的遍历 遍历定义:从已给的连通图中某一顶点出发,沿着一些边,访 遍图中所有的顶点,且使每个顶点仅被访问一次,就叫做 图的遍历,它是图的基本运算。 遍历实质:找每个顶点的邻接点的过程。 图的特点:图中可能存在回路,且图的任一顶点都可能与其它 顶点相通,在访问完某个顶点之后可能会沿着某些边又回 到了曾经访问过的顶点。 解决思路:可设置一个辅助数组 visited [n ],用来标记每个被 访问过的顶点。它的初始状态为0,在图的遍历过程中, 一旦某一个顶点i被访问,就立即改 visited [i]为1,防止它 被多次访问。 图常用的遍历: 怎样避免重复访问?
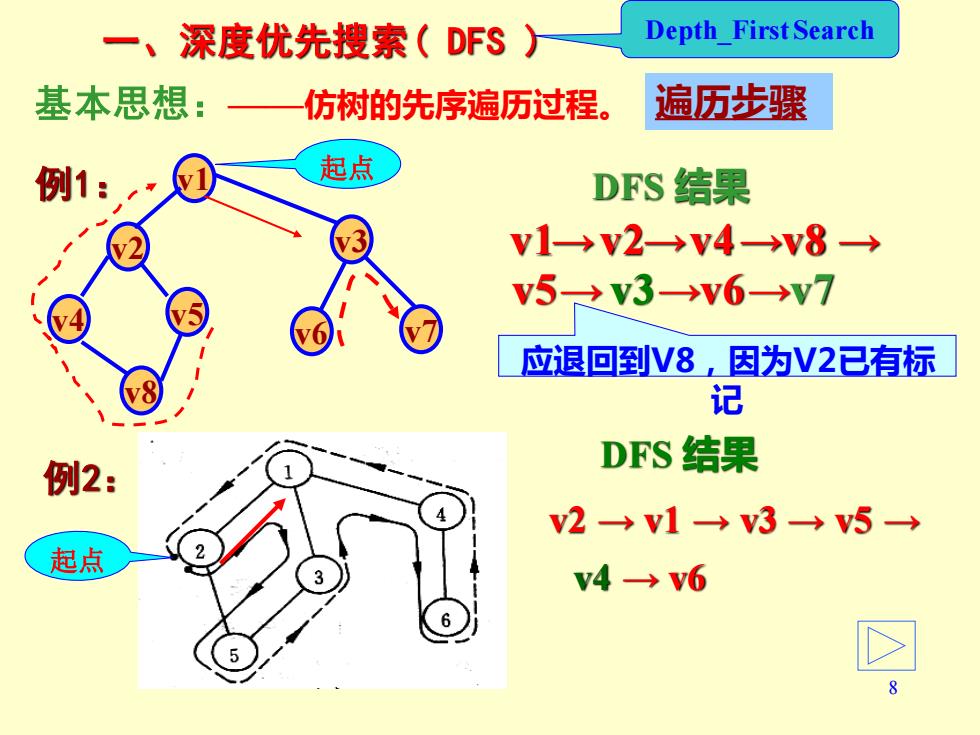
一、深度优先搜索(DFS) Depth First Search 基本思想: 仿树的先序遍历过程。 遍历步骤 例1: 起点 DFS结果 v1-→V2→V4→v8 → v5→v3V6→y7 76 应退回到V8,因为V2已有标 记 例2: DFS结果 v2→v1→v3→v5→ 起点 v4→v6
8 一、深度优先搜索( DFS ) 基本思想:——仿树的先序遍历过程。 Depth_First Search v1 v1 v2 v3 v8 v6 v7 v4 v5 例1: DFS 结果 → → → → → → → v2 v4 v8 v5 v3 v6 v7 例2: v2 → v1 → v3 → v5 → DFS 结果 v4 → v6 起点 起点 遍历步骤 应退回到V8,因为V2已有标 记

深度优先搜索(遍历)步骤: 简单归纳: 访问起始点v; 若v的第1个邻接点没访问过,深度遍历此邻接点; 若当前邻接点已访问过,再找ν的第2个邻接点重新遍历。 详细归纳: ◆在访问图中某一起始顶点v后,由y出发,访问它的任一邻接 顶点w1: ◆再从W出发,访问与w,邻接但还未被访问过的顶点w2; ◆然后再从w出发,进行类似的访问,. ◆如此进行下去,直至到达所有的邻接顶点都被访问过的顶点 为止。 ◆接着,退回一步,退到前一次刚访问过的顶点,看是否还有其 它未被访问的邻接顶点。 如果有,则访问此顶点,之后再从此顶点出发,进行与前述 类似的访问: 如果没有,就再退回一步进行搜索。重复上述过程,直到连 通图中所有顶点都被访问过为止
9 深度优先搜索(遍历)步骤: 详细归纳: 在访问图中某一起始顶点 v 后,由 v 出发,访问它的任一邻接 顶点 w1; 再从 w1 出发,访问与 w1邻接但还未被访问过的顶点 w2; 然后再从 w2 出发,进行类似的访问,. 如此进行下去,直至到达所有的邻接顶点都被访问过的顶点 u 为止。 接着,退回一步,退到前一次刚访问过的顶点,看是否还有其 它未被访问的邻接顶点。 如果有,则访问此顶点,之后再从此顶点出发,进行与前述 类似的访问; 如果没有,就再退回一步进行搜索。重复上述过程,直到连 通图中所有顶点都被访问过为止。 简单归纳: • 访问起始点v; • 若v的第1个邻接点没访问过,深度遍历此邻接点; • 若当前邻接点已访问过,再找v的第2个邻接点重新遍历