
3、一元二次方程 y=bo+bx+b2x2 b=不施肥产量,b1、b2=效应系数,b=起始时肥料增产效应的 趋势;b,=肥料效应增减的程度,反映效应曲线的曲率变化
3、一元二次方程 y=b0+b1x+b2x 2 b0=不施肥产量,b1、b2=效应系数,b1=起始时肥料增产效应的 趋势;b2=肥料效应增减的程度,反映效应曲线的曲率变化
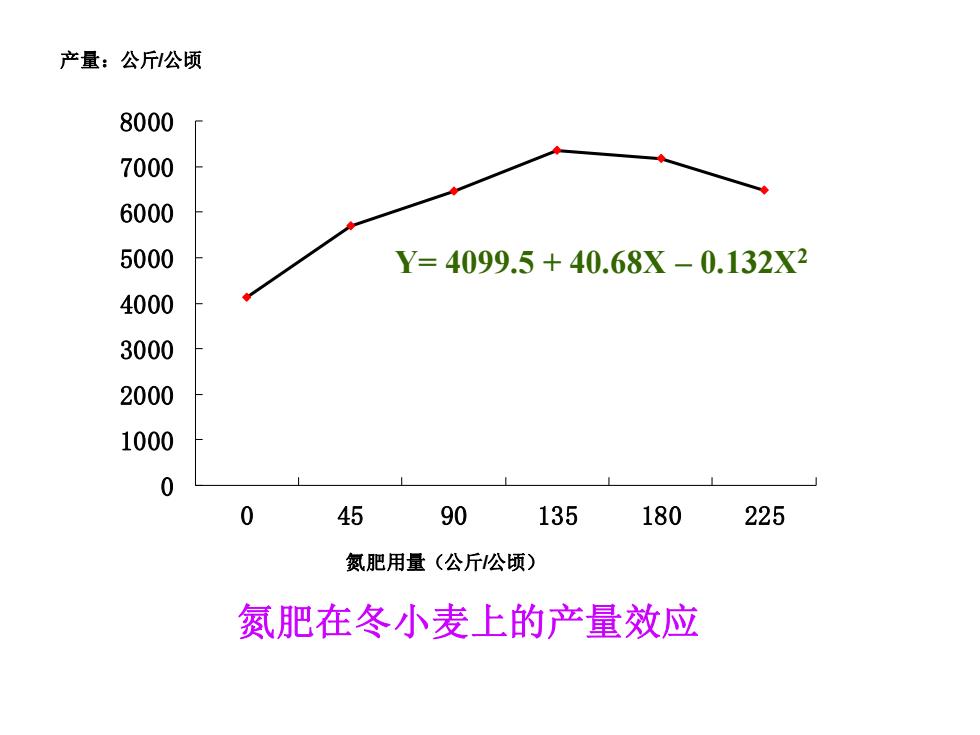
产量:公斤公顷 8000 7000 6000 5000 Y=4099.5+40.68X-0.132X2 4000 3000 2000 1000 0 0 45 90 135 180 225 氮肥用量(公斤公顷) 氮肥在冬小麦上的产量效应
0 1000 2000 3000 4000 5000 6000 7000 8000 0 45 90 135 180 225 氮肥在冬小麦上的产量效应 产量:公斤/公顷 氮肥用量(公斤/公顷) Y= 4099.5 + 40.68X – 0.132X2

3、一元二次方程 y=bo+bx+b2x2 当b>0,b2<0时,施肥量与产量呈现为二次抛物线形式。作物的产量随施 肥的增加按递减率增加,超过最高产量后产量随施肥量的增加而减少, 二次抛物线函数可反映出超过最高产量后总产量的递减效应 dy/dx=边际产量,当x=0时,dy/dk=b1,其生物学意义是起始时增施肥料 的增产量,一般为为正值 当dy/dk=0,dy/dPx=2b2>0时,函数有一个极小值,曲线呈现报酬递增型 当dy/dk=0,dy/dPx=2b2<0时,函数有一个极大值,曲线呈现报酬递减型 最高产量施肥量x=b1/2b2
3、一元二次方程 y=b0+b1x+b2x 2 当b1>0, b2<0时,施肥量与产量呈现为二次抛物线形式。作物的产量随施 肥的增加按递减率增加,超过最高产量后产量随施肥量的增加而减少, 二次抛物线函数可反映出超过最高产量后总产量的递减效应 dy/dx=边际产量,当x=0时, dy/dx=b1,其生物学意义是起始时增施肥料 的增产量,一般为为正值 当dy/dx=0,d 2y/d2x=2b2>0时,函数有一个极小值,曲线呈现报酬递增型 当dy/dx=0,d 2y/d2x=2b2<0时,函数有一个极大值,曲线呈现报酬递减型 最高产量施肥量x=b1 /2b2

4、二元二次方程 y=b0+b1x1+b2X12+b3X2+b4X22+b5X1X2 b为不施肥时的产量,b1b2为x1的主效应系数,b3b4为x2 的主效应系数,b为x和x的交互效应系数
4、二元二次方程 y=b0+b1x1+b2x1 2+b3x2+b4x2 2+b5x1x2 b0为不施肥时的产量,b1、b2为x1的主效应系数,b3、b4为x2 的主效应系数,b5为x1和x2的交互效应系数

5、三元二次方程 y=b0+b1X1+b2X12+b3X2+b4X22+b5X3+b6X32 +b-XX2+b8XjX3+b9X2X3 其中: b1、b2b3、b4、b5、b6分别为x1x2 x3的主效应系数,b7、bg、bg为交互效应系 数
5、三元二次方程 y=b0+b1x1+b2x1 2+b3x2+b4x2 2+b5x3+b6x3 2 +b7x1x2+b8x1x3+b9x2x3 其中: b1、b2、b3、b4、b5、b6分别为x1、x2、 x3的主效应系数,b7、b8、b9为交互效应系 数