
4.吉布斯-杜亥姆方程 偏摩尔量集合公式 X=∑nBXR 对集合公式微分 dK=立n,Kn+2Xnd血n 因 dX=∑XpdnB B=1 ∑ndXg=0 Gibbs-Duhem方程 21
21 4. 吉布斯-杜亥姆方程 偏摩尔量集合公式 = = k B 1 X nB XB = = B 1 dX XB dn B B k B B k B dX = nB dXB +X dn 对集合公式微分 因 = k B nB dXB 0 Gibbs-Duhem方程

x,dZnm=0 R-1 也称吉布斯-杜亥姆方程。 吉布斯-杜亥姆方程表明:多组分体 系中各物质的偏摩尔量之间不是彼此无 关的,而是有一定的联系的。如有某一 组分的偏摩尔量增加,必有一个或多个 组分的偏摩尔量减少,其变化量服从吉 布斯-杜亥姆方程
22 = = k B 1 x B dZB,m 0 也称吉布斯-杜亥姆方程。 吉布斯-杜亥姆方程表明:多组分体 系中各物质的偏摩尔量之间不是彼此无 关的,而是有一定的联系的。如有某一 组分的偏摩尔量增加,必有一个或多个 组分的偏摩尔量减少,其变化量服从吉 布斯-杜亥姆方程

5.各偏摩尔量之间的关系 根据各函数定义 H=U+PV A=U-TS G=H-TS=U+PV-TS=A+PV 所以 23
23 5. 各偏摩尔量之间的关系 G = H-TS = U+PV-TS = A+PV H = U+PV A = U-TS 根据各函数定义 所以
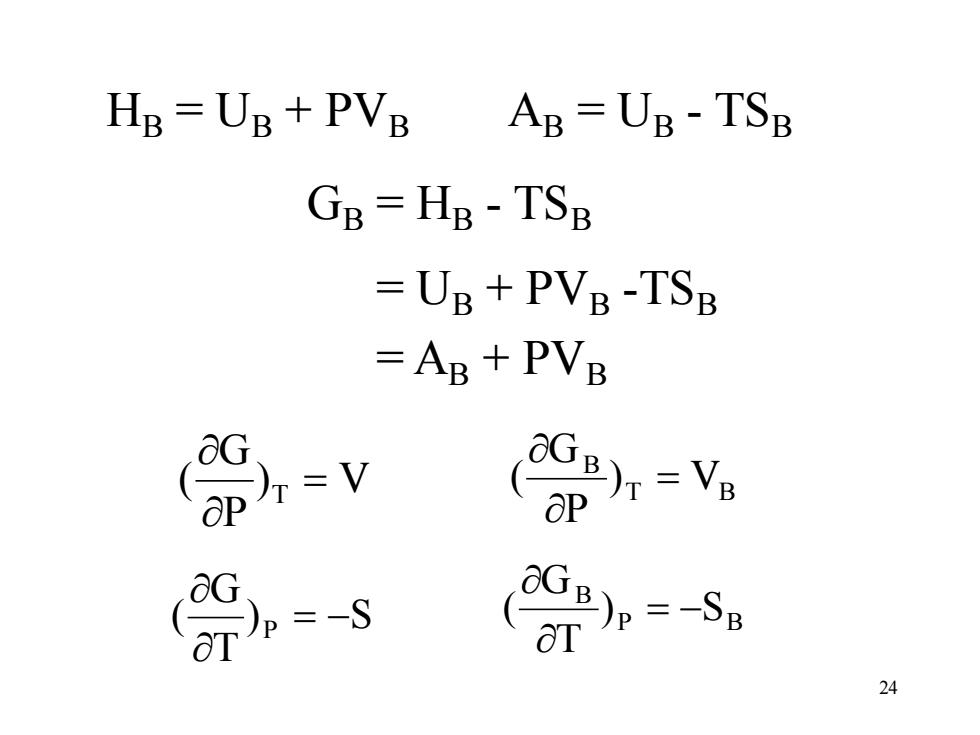
HB=UB+PVB AB-UB-TSB GB-HB-TSB UB PVB-TSB =AB +PVB (v ()V, 24
24 GB = HB - TSB HB = UB + PVB AB = UB - TSB = UB + PVB -TSB = AB + PVB ) V P G ( T = T B B ) V P G ( = ) S T G ( P = − P B B ) S T G ( = −

§4.2 化学势 对于多组分体系,另一个重要的物 理量就是化学势。 对单组分体系,在等温等压且无其 他功的情况下: 不可逆,自发 dG≤0 可逆,平衡 25
25 §4.2 化学势 对于多组分体系,另一个重要的物 理量就是化学势。 对单组分体系,在等温等压且无其 他功的情况下: dG ≤ 0 不可逆,自发 可逆,平衡