
·家庭作业·数学·五年级·下册·配人教版· ● 第7课时 解决问题 基)础梳理) 能力提升) 一、你能想办法求出下面两种物体的体积吗? 三、解决问题。 L.在一个长6dm、宽4dm、深3dm的长方体玻 璃缸中注满水,然后把一块棱长2.1dm的正 橡皮泥 石块 方体石块放入水中,玻璃缸中溢出的水的体积 可以把橡皮泥捏成规则的长方体或正方 体,再测量它的长、宽、高,然后根据 是多少? 长方体的体积=长×宽×高 2.1×2.1×2.1=9.261(dm3) 就可以求出橡皮泥的体积。 石块的形状不能改变,可以用排水法。 先测量出水的体积,然后把石块放入水中 2.佳佳想知道一个瓷碗的体积,于是准备了一个 (完全浸没,水没有溢出),再测量出水和 盛了适量水的长方体玻璃容器和一块体积为 石块的总体积,最后两者的差就是石 块的体积。 1dm的金属块,把金属块完全浸没在水中,水 二、做实验。 面上升了16cm,然后又放入瓷碗,完全浸没 1.一个从里面量长50cm、宽40cm、高30cm的 后,水面又上升了4cm,则瓷碗的体积是多少? 长方体鱼缸中,水深25cm,放入一些金鱼后, 1dm3=1000cm 水面上升3cm,这些金鱼的体积是多少立方 1000÷16×4=250(cm3) 厘米? 50×40×3=6000(cm3) 智慧拓展) 四、做一做。 一个无水观赏鱼缸 (无盖)中放有一块高 2.有一个从里面量长8dm、宽5dm的长方体玻 为14cm、体积为 1100cm3的假山石 璃缸,将一块假山石放到里面后,水面上升 cm 46 cm 2cm(水面淹过假山石,水没有溢出),这块假 (如右图),如果水管 以每分钟6dm3的流量向鱼缸内注水,那么 山石的体积是多少立方分米? 8×5×(2÷10)=8(dm3) 至少需要多长时间才能将假山石完全淹没? 46×25×14-1100=15000(cm3) 15000cm3=15dm3 15÷6=2.5(分) 0.5L=(500)mL600mL=(0.6)L4L=(4000)mL2.4L=(2400)mL 主题口算 24 4700mL=(4.7)L750mL=(0.75)L1.07m2=(1070)dm3=(1070)L

·3长方体和正方体。 整理和复习 一、在下面的表格里填上合适的数。 (2)此时,将一块铁块全部浸人水中,水面离容器 长 宽/ 底面积 高/ 表面积 体积 口还有2.4dm,你能求出该铁块的体积吗? 名称 cm cm cm2 cm cm2 cm2 4-2.4=1.6(dm) 7.2 4.5 32.4 2.4 120.96 77.76 2.5×2×1.6=8(dm3) 长方体 4.5 36 6 197 180 正方体 7 > 49 > 294 343 3.王叔叔家买了一个柜子(如 二、填一填。 图,单位:cm),要在这个柜 L.一个长12cm、宽9cm、高7cm的长方体的六 子的外面贴上一层装饰板 个面中,最大面的面积是(108cm2),最小面 (底面不贴)。如果每平方 30e 的面积是(63cm2)。 米装饰板220元,购买装饰板需要多少钱? 2.一个无盖的正方体水槽的表面积是20dm,这 80×(30+30)×3+30×30×6=19800(cm2) 个水槽的底面积是(4)dm,容积是(8)L。 19800cm2=1.98m2 3.3650cm3=(3650)mL=(3.65)L 220×1.98=435.6(元) 8509dm3=(8)m3(509)dm 736cm2=(7.36)dm22030mL=(2.03)L 4.用2cm厚的铁板做一个长方体铁箱(有盖), 三、解决问题。 铁箱长6dm,宽5dm,高4dm,求这个铁箱的 1.实验小学要建一个长60m、宽50m的长方形 体积和容积。 足球场,先要铺5cm厚的煤渣,再铺12cm厚 体积:6×5×4=120(dm3) 的三合土。需要煤渣和三合土各多少立方米? 2 cm=0.2 dm 5cm=0.05m 容积:(6-0.2×2)×(5-0.2×2)×(4-0.2× 12cm=0.12m 2)=92.736(dm3) 煤渣:60×50×0.05=150(m3) 三合土:60×50×0.12=360(m3) 四、做一做。 2.把10L水倒入一个长为2.5dm,宽为2dm, 如下图所示,玻璃容器的底面积是80cm(不 高为6dm的长方体水缸中。 计玻璃厚度)。观察图中玻璃容器内水位的 (1)这时水面的高度离容器口有多少分米? 变化,求大圆球的体积。 10L=10dm 10÷(2.5×2)=2(dm) 6-2=4(dm) 80×(18-12)÷2=240(cm3) 80×(38-12)-240×3=1360(cm3) 主题口算 0.6×2.5=1.5 7×0.03=0.21 12.5÷2.5=5 2.8×0.3=0.84 25 4.5÷0.01=450 1.8×50=90 64÷1.6=40 0.48×0.2=0.096

。家庭作业·数学·五年级·下册·配人教版· ● 第3单元总结 ⑥复习梳理0 知识点 概要 (1)长方体的特点:①长方体有8个顶点。②长方体有12条棱,相对的棱长度相等。③长 方体有6个面,每个面都是长方形(特殊情况有两个相对的面是正方形),相对的面完全 相同。 1.长方体和正 (2)相交于同一顶点的3条棱的长度分别叫作长方体的长、宽、高。 方体的认识 (3)正方体的特点:①正方体有8个顶点。②正方体有12条棱,所有棱的长度相等。③正 方体有6个面,每个面都是正方形且完全相同。 (4)正方体是长、宽、高都相等的长方体 2.长方体和正方 (1)长方体的棱长总和=(长十宽+高)×4。 体的棱长总和 (2)正方体的棱长总和=棱长×12 (1)定义:长方体或正方体6个面的面积之和,叫作它的表面积。 3.长方体和正 (2)长方体的表面积=(长×宽+长×高+宽×高)×2。 方体的表面积 (3)正方体的表面积=棱长×棱长×6 4.体积和体积 (1)物体所占空间的大小叫作物体的体积。 单位 (2)常用的体积单位有立方厘米、立方分米和立方米,可以分别写成cm3、dm3和m3 (1)长方体的体积=长×宽×高,用字母表示为V=abh。 5.长方体和正 (2)正方体的体积=棱长×棱长×棱长,用字母表示为V=a·a·a=a3。 方体的体积 (3)长方体或正方体的体积=底面积×高,用字母表示为V=S 6.容积和容积 (1)像太空舱、粮仓、油桶、盒子等所能容纳物体的体积,通常叫作它们的容积。 单位 (2)计量容积,一般用体积单位。计量液体的体积,常用容积单位升(L)和毫升(mL) 7.单位换算 1m3=1000dm,1dm3=1000cm,1L=1000mL,1L=1dm3,1mL=1cm C易错易混○ 1.没有准确掌握长方体或正方体的特征 判断:(1)长方体的6个面一定是长方形。(×) (2)一般的长方体最多可以有4个面是正方形。(×) (3)6个正方形能围成一个正方体。(×) 易错警示:(1)常因忽视长方体的面的特殊情况而出错。特殊情况下,长方体可以有两个相对的面 17×4=68 10×12=120 2.8×4=11.2 11×4=44 主题口算 26 9.6÷4=2.4 192÷4=48 0.3×8=2.4 35.2÷4=8.8

。3长方体和正方体。 是正方形。(2)应注意有4个面是正方形的长方体一定是正方体,一般的长方体最多有两个相对的 面是正方形。(3)正方体的6个面是完全相同的正方形,而题中没有说明6个正方形的大小是否相 同,所以错误。 2.长方体(或正方体)的切割问题中,不理解增加或减少的表面积是哪部分面积 解答:一个长方体,沿着平行于底面的方向切掉高为3cm的一部分,剩下的部分正好是一个正方 体,但表面积减少了72c,原来长方体的表面积是多少? 易错警示:此类问题易因不理解增加或减少的表面积是哪部分而出错。根据题 cm 意,画出示意图,如图所示,可知切掉的部分是一个长方体,底面是正方形,高是 3cm,剩下的正方体的表面积与原来长方体的表面积相比较,减少的部分即切 掉的长方体前、后、左、右4个面的面积之和,且这4个面完全相同。由此可知, 切掉的长方体的底面周长为72÷3=24(cm),则底面边长为24÷4=6(cm),即 原来长方体的底面边长为6cm,原来长方体的高为6十3=9(cm),进而可求出原来长方体的表 面积。 72÷3=24(cm)24÷4=6(cm) 6+3=9(cm) 6×6×2+6×9×4=288(cm2) 3.没有准确掌握排水法的本质 解答:在一个长7m、宽4m、深1m的水池中注满水,然后把两根长2m、宽1.5m、高2m的石柱 竖着放入水池中。水池溢出的水的体积是多少? 易错警示:往注满水的容器中放入物体,当物体完全浸入水中时,溢出的水的体积等于放入物体的 体积;当物体不完全浸入水中时,溢出的水的体积等于放入物体浸入水中部分的体积。 2×1.5×1×2=6(m3) 主题口算 0.5×12=60.36÷12=0.03 2.5÷5×0.8=0.41.6÷0.4×5=20 27 84×0.5=423.6×10=36 0.6÷3×0.2=0.041.25×8×2=20
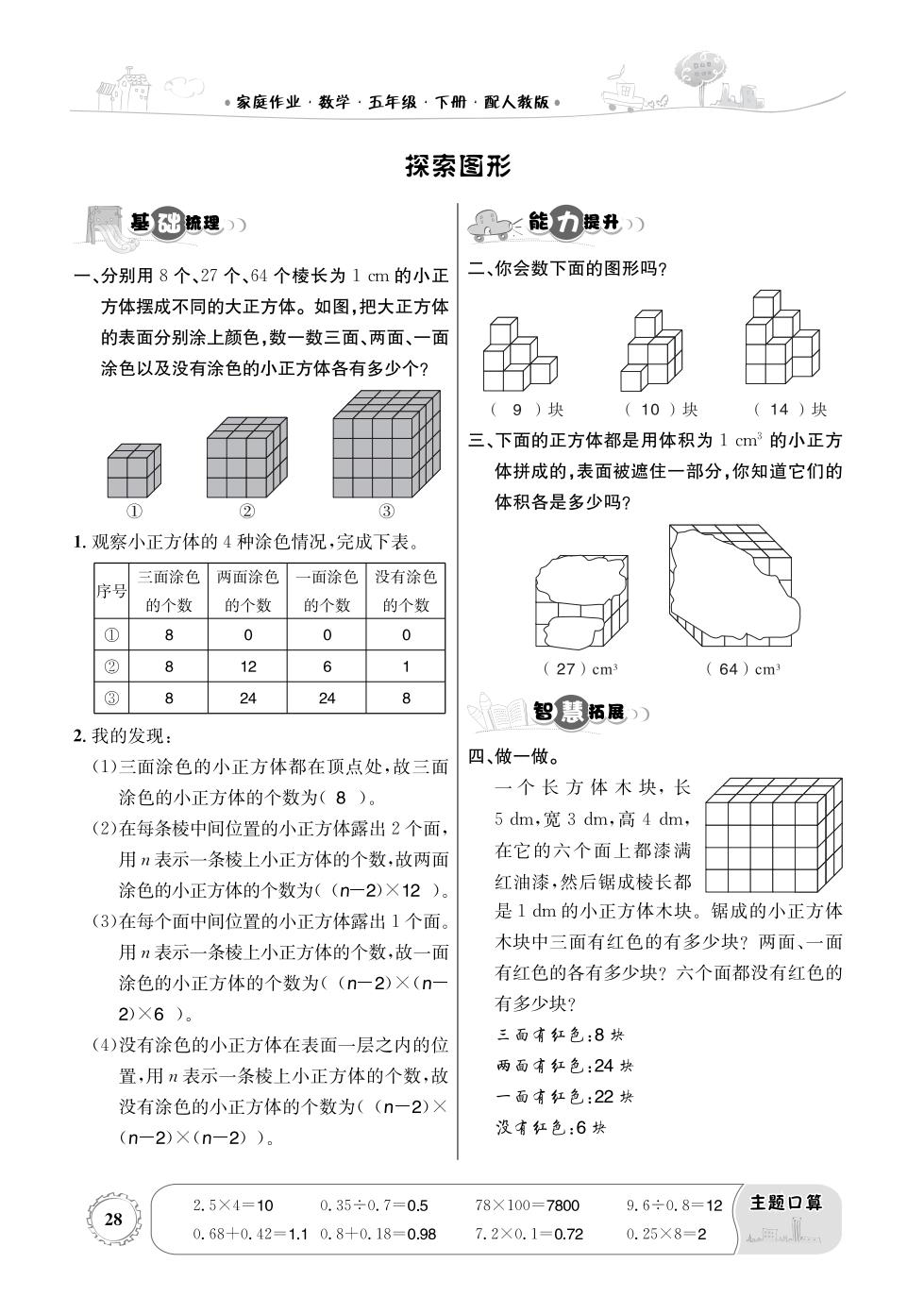
。家庭作业·数学·五年级·下册·配人教版· 探索图形 基)础梳理) 2长能力提升) 一、分别用8个、27个、64个棱长为1cm的小正 二、你会数下面的图形吗? 方体摆成不同的大正方体。如图,把大正方体 的表面分别涂上颜色,数一数三面、两面、一面 涂色以及没有涂色的小正方体各有多少个? (9)块 (10)块 (14)块 三、下面的正方体都是用体积为1cm3的小正方 体拼成的,表面被遮住一部分,你知道它们的 ① ② ③ 体积各是多少吗? 1.观察小正方体的4种涂色情况,完成下表。 三面涂色 两面涂色 一面涂色 没有涂色 序号 的个数 的个数 的个数 的个数 ① 8 0 0 0 T个工 ② 8 12 6 1 (27)cm (64)cm3 ③ 8 24 24 智慧拓展) 2.我的发现: (1)三面涂色的小正方体都在顶点处,故三面 四、做一做。 涂色的小正方体的个数为(8)。 一个长方体木块,长 (2)在每条棱中间位置的小正方体露出2个面, 5dm,宽3dm,高4dm, 用n表示一条棱上小正方体的个数,故两面 在它的六个面上都漆满 涂色的小正方体的个数为((n一2)×12)。 红油漆,然后锯成棱长都 (3)在每个面中间位置的小正方体露出1个面。 是1dm的小正方体木块。锯成的小正方体 用n表示一条棱上小正方体的个数,故一面 木块中三面有红色的有多少块?两面、一面 涂色的小正方体的个数为((n一2)×(n一 有红色的各有多少块?六个面都没有红色的 2)×6)。 有多少块? (4)没有涂色的小正方体在表面一层之内的位 三面有红色:8块 置,用n表示一条棱上小正方体的个数,故 两面有红色:24块 没有涂色的小正方体的个数为((n一2)× 一面有红色:22块 (n-2)×(n-2))。 没有红色:6块 2.5×4=10 0.35÷0.7=0.5 78×100=7800 9.6÷0.8=12 主题口算 28 0.68+0.42=1.10.8+0.18=0.98 7.2×0.1=0.72 0.25×8=2