
再例:8个品种4个重复的随机区组排列图16个品种3个重复的随机区组, 小区布置成两排略 2.随机区组设计优、缺点 优点: ①易设计和分析,能保证试验的精确度和准确度(贯彻了三原则)。 ②对试验条件要求不高,灵活性大,适用广。 ③单因素、多因素试验都可应用。 缺点: ①不允许处理数太多,一般少于20 ②试验精确度没有拉丁方设计高。 (三)拉丁方设计 拉丁方设计实行双重局部控制,精确度最高,是随机区组设计特殊情况。 1.实施方法 从行和列两个方向上排列成区组,而每一处理在每一行或列都只占有一个小 教 区,处理在各区组的排列是随机的。 2.拉丁方设计的特占: 处理数=重复数=行区组数=列区组数:精确度高:试验结果分析简便: 3.随机排列的方法 均由标准拉丁丁方衍变而来 由于拉丁方的排列方式很多,抽签也麻烦,为了简便又体现随机排列原则 采用办法: 1从书中选一标准拉丁方 2.按规则随机调动直行、横行及处理 4.实际应用:(课件有彩图) 例1.不同捕蛾灯效果比较试验(灯位、日期) 2.烟叶毒素病不同毒素浓度诱病试验(株、层) 5.拉丁方设计的优、缺点: 优点:精确度最高,适用试验存在两种系统误差的试验 缺点:1.缺乏伸缩性:处理数=重复数=行数=列数 这种试验设计,不能将一行或一列分开设置:观察记载和田间管理都不方便 2.处理数限于5一8
16 教 学 过 程 再例:8 个品种 4 个重复的随机区组排列 图 16 个品种 3 个重复的随机区组, 小区布置成两排略 2.随机区组设计优、缺点 优点: ①易设计和分析,能保证试验的精确度和准确度(贯彻了三原则)。 ②对试验条件要求不高,灵活性大,适用广。 ③单因素、多因素试验都可应用。 缺点: ①不允许处理数太多,一般少于 20。 ②试验精确度没有拉丁方设计高。 (三)拉丁方设计 拉丁方设计实行双重局部控制,精确度最高,是随机区组设计特殊情况。 1.实施方法 从行和列两个方向上排列成区组,而每一处理在每一行或列都只占有一个小 区,处理在各区组的排列是随机的。 2. 拉丁方设计的特点: 处理数=重复数=行区组数=列区组数;精确度高;试验结果分析简便; 3.随机排列的方法 均由标准拉丁方衍变而来 由于拉丁方的排列方式很多,抽签也麻烦,为了简便又体现随机排列原则, 采用办法: 1.从书中选一标准拉丁方 2.按规则随机调动直行、横行及处理 4.实际应用:(课件有彩图) 例1.不同捕蛾灯效果比较试验(灯位、日期) 2.烟叶毒素病不同毒素浓度诱病试验(株、层) 5.拉丁方设计的优、缺点: 优点:精确度最高,适用试验存在两种系统误差的试验。 缺点: 1.缺乏伸缩性 :处理数=重复数=行数=列数 这种试验设计,不能将一行或一列分开设置;观察记载和田间管理都不方便。 2.处理数限于5-8
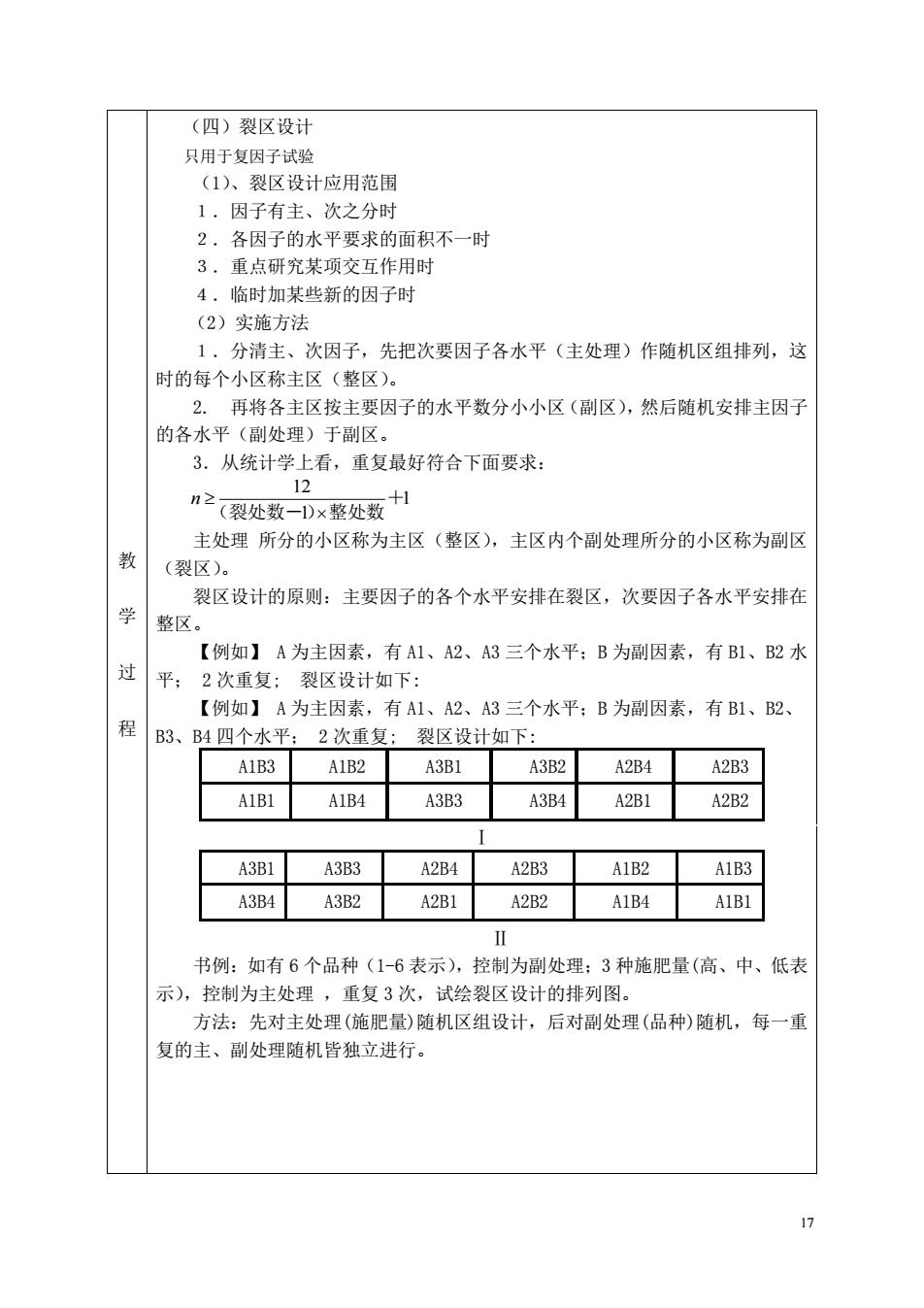
(四)裂区设计 只用于复因子试验 (1)、裂区设计应用范围 1.因子有主、次之分时 2.各因子的水平要求的面积不一时 3,重点研究某项交互作用时 4.临时加某些新的因子时 (2)实施方法 1,分清主、次因子,先把次要因子各水平(主处理)作随机区组排列,这 时的每个小区称主区(整区)。 2.再将各主区按主要因子的水平数分小小区(副区),然后随机安排主因子 的各水平(副处理)于副区。 3.从统计学上看,重复最好符合下面要求: ”之(裂处数-×整处数刊 主处理所分的小区称为主区(整区),主区内个副处理所分的小区称为副区 教 (裂区)。 裂区设计的原则:主要因子的各个水平安排在裂区,次要因子各水平安排在 整区。 【例如】A为主因素,有A1、A2、A3三个水平;B为副因素,有B1、B2水 过 平;2次重复:裂区设计如下: 【例如】A为主因素,有A1、A2、A3三个水平:B为副因素,有B1、B2、 程 B3、B4四个水平: 2次重复 裂风设计如下 A1B3 A1B2 A3B1 A3B2 A2B4 A2B3 A1B1 A1B4 A3B3 A3B4 A2BI A2B2 A3B1 A3B3 A2B4 A2B3 A1B2 A1B3 A3B4 A3B2 A2B1 A2B2 A1B4 A1B1 书例:如有6个品种(1-6表示),控制为副处理:3种施肥量(高、中、低表 示),控制为主处理,重复3次,试绘裂区设计的排列图。 方法:先对主处理(施肥量)随机区组设计,后对副处理(品种)随机,每一重 复的主、副处理随机皆独立进行 17
17 教 学 过 程 (四)裂区设计 只用于复因子试验 (1)、裂区设计应用范围 1.因子有主、次之分时 2.各因子的水平要求的面积不一时 3.重点研究某项交互作用时 4.临时加某些新的因子时 (2)实施方法 1.分清主、次因子,先把次要因子各水平(主处理)作随机区组排列,这 时的每个小区称主区(整区)。 2. 再将各主区按主要因子的水平数分小小区(副区),然后随机安排主因子 的各水平(副处理)于副区。 3.从统计学上看,重复最好符合下面要求: 1 1 12 + (裂处数-)整处数 n 主处理 所分的小区称为主区(整区),主区内个副处理所分的小区称为副区 (裂区)。 裂区设计的原则:主要因子的各个水平安排在裂区,次要因子各水平安排在 整区。 【例如】 A 为主因素,有 A1、A2、A3 三个水平;B 为副因素,有 B1、B2 水 平; 2 次重复; 裂区设计如下: 【例如】 A 为主因素,有 A1、A2、A3 三个水平;B 为副因素,有 B1、B2、 B3、B4 四个水平; 2 次重复; 裂区设计如下: A1B3 A1B2 A3B1 A3B2 A2B4 A2B3 A1B1 A1B4 A3B3 A3B4 A2B1 A2B2 Ⅰ A3B1 A3B3 A2B4 A2B3 A1B2 A1B3 A3B4 A3B2 A2B1 A2B2 A1B4 A1B1 Ⅱ 书例:如有 6 个品种(1-6 表示),控制为副处理;3 种施肥量(高、中、低表 示),控制为主处理 ,重复 3 次,试绘裂区设计的排列图。 方法:先对主处理(施肥量)随机区组设计,后对副处理(品种)随机,每一重 复的主、副处理随机皆独立进行
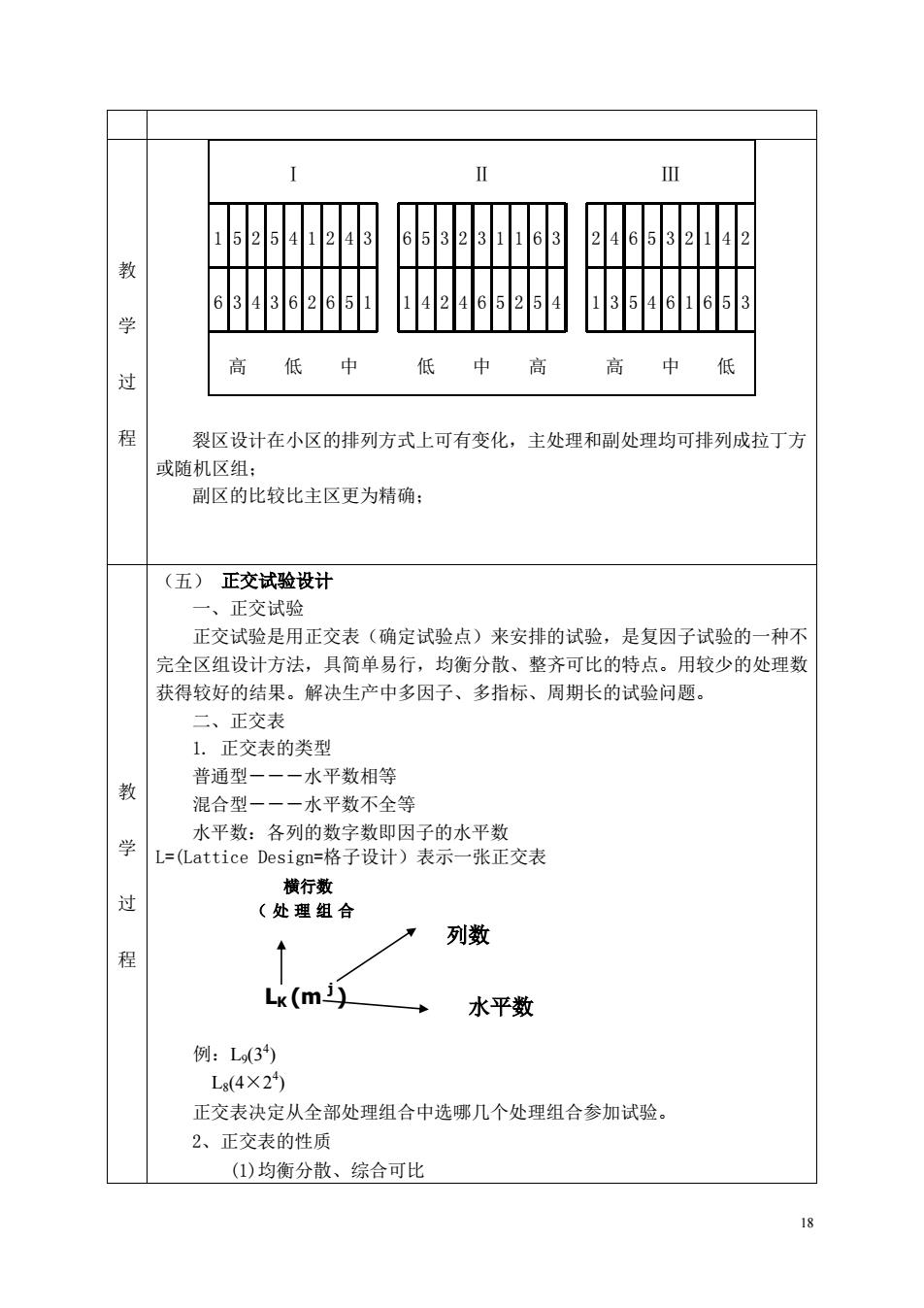
高 低 中 低 中高 高中低 过 程 裂区设计在小区的排列方式上可有变化,主处理和副处理均可排列成拉丁方 或随机区组: 副区的比较比主区更为精确 (五)正交试验设计 一、正交试验 正交试验是用正交表(确定试验点)来安排的试验,是复因子试验的一种不 完全区组设计方法,具简单易行,均衡分散、整齐可比的特点。用较少的处理数 获得较好的结果。解决生产中多因子、多指标、周期长的试验问题。 二、正交表 1.正交表的类型 普通型一一一水平数相等 混合型一一一水平数不全等 水平数:各列的数字数即因子的水平数 学 L=(Lattice Design=格子设计)表示一张正交表 横行数 (处理组合 ·列数 ↑ Lk(m) 水平数 例:L(3 L(4X2 正交表决定从全部处理组合中选哪几个处理组合参加试验。 2、正交表的性质 (1)均衡分散、综合可比
18 教 学 过 程 Ⅰ Ⅱ Ⅲ 1 5 2 5 4 1 2 4 3 6 5 3 2 3 1 1 6 3 2 4 6 5 3 2 1 4 2 6 3 4 3 6 2 6 5 1 1 4 2 4 6 5 2 5 4 1 3 5 4 6 1 6 5 3 高 低 中 低 中 高 高 中 低 裂区设计在小区的排列方式上可有变化,主处理和副处理均可排列成拉丁方 或随机区组; 副区的比较比主区更为精确; 教 学 过 程 (五) 正交试验设计 一、正交试验 正交试验是用正交表(确定试验点)来安排的试验,是复因子试验的一种不 完全区组设计方法,具简单易行,均衡分散、整齐可比的特点。用较少的处理数 获得较好的结果。解决生产中多因子、多指标、周期长的试验问题。 二、正交表 1. 正交表的类型 普通型---水平数相等 混合型---水平数不全等 水平数:各列的数字数即因子的水平数 L=(Lattice Design=格子设计)表示一张正交表 例:L9(34 ) L8(4×2 4 ) 正交表决定从全部处理组合中选哪几个处理组合参加试验。 2、正交表的性质 (1)均衡分散、综合可比 横行数 (处理组合 数) LK (m j ) 列数 水平数

正交表中: 1.每一列中,不同数字出现的次数相等 2.任意两列中,每种有序数对出现的次数相等 这种性质即正交性,它决定了每个因子各水平的重复次数相等,并且和个处理 组合出现的次数也相等。因而使得正交设计具有均衡分散、整齐可比的特性。 (2)可伸可缩,效应明确 例如:L(3 三、选用正交表设计试验方案的步骤 第一步挑因水、选水平(专业知识) 第二步选一张适合的正交表 所选正交必须符合两个条件: 1.正交表各列的水平数必须等于和研究因子水平数 2.正交表自由度≥∑df子+∑df红 正交表总自由度=横行数一1 教 **分考察交互作用和不考察交互作用两种情况 第三步作表头设计 将各因子及各项交互作用安排在正交表的列上 如试验处理组合数过多,可按某空白列下的水平号将全部处理组合分几个组, 过每组为1个不完全区组。 第四步写试验方案 程 四、选用正交表设计试验方案的实例 实例一:不考虑互作 [例13.11]有一小麦栽培试验,A因素为施碳铵方式,4水平:B因素为追 肥时期,2水平:C因素为基肥多少,2水平:D因素为镇压次数,2水平:E因 素为种子处理,2水平,据以往经验,不存在互作,现要求明确各因素主效,试 予设计。 所选正交必须符合两个条件: 1.正交表各列的水平数必须等于和研究因子水平数一一混合型正交表 2.正交表自由度≥∑df各因子+Σdf各互作=3+1+1+1+1=7正交表横行数 ≥8 .L(4×2)附表13正交表 (9)L.(4×2) 作表头设计如下,试验方案略
19 教 学 过 程 正交表中: 1.每一列中,不同数字出现的次数相等 2.任意两列中,每种有序数对出现的次数相等 这种性质即正交性,它决定了每个因子各水平的重复次数相等,并且和个处理 组合出现的次数也相等。因而使得正交设计具有均衡分散、整齐可比的特性。 (2)可伸可缩,效应明确 例如:L9(34 ) 三、选用正交表设计试验方案的步骤 第一步 挑因水、选水平(专业知识) 第二步 选一张适合的正交表 所选正交必须符合两个条件: 1.正交表各列的水平数必须等于和研究因子水平数 2.正交表自由度≥∑df 各因子+∑df 各互作 正交表总自由度=横行数-1 **分考察交互作用和不考察交互作用两种情况 第三步 作表头设计 将各因子及各项交互作用安排在正交表的列上 如试验处理组合数过多,可按某空白列下的水平号将全部处理组合分几个组, 每组为 1 个不完全区组。 第四步 写试验方案 四、选用正交表设计试验方案的实例 实例一:不考虑互作 [例 13.11] 有一小麦栽培试验,A 因素为施碳铵方式,4 水平;B 因素为追 肥时期,2 水平;C 因素为基肥多少,2 水平;D 因素为镇压次数,2 水平;E 因 素为种子处理,2 水平,据以往经验,不存在互作,现要求明确各因素主效,试 予设计。 所选正交必须符合两个条件: 1.正交表各列的水平数必须等于和研究因子水平数-混合型正交表 2.正交表自由度≥∑df 各因子+∑df 各互作=3+1+1+1+1=7 正交表横行数 ≥8 ∴L8(4×2 4) 附表 13 正交表 (9)L8(4×2 4) 作表头设计如下,试验方案略
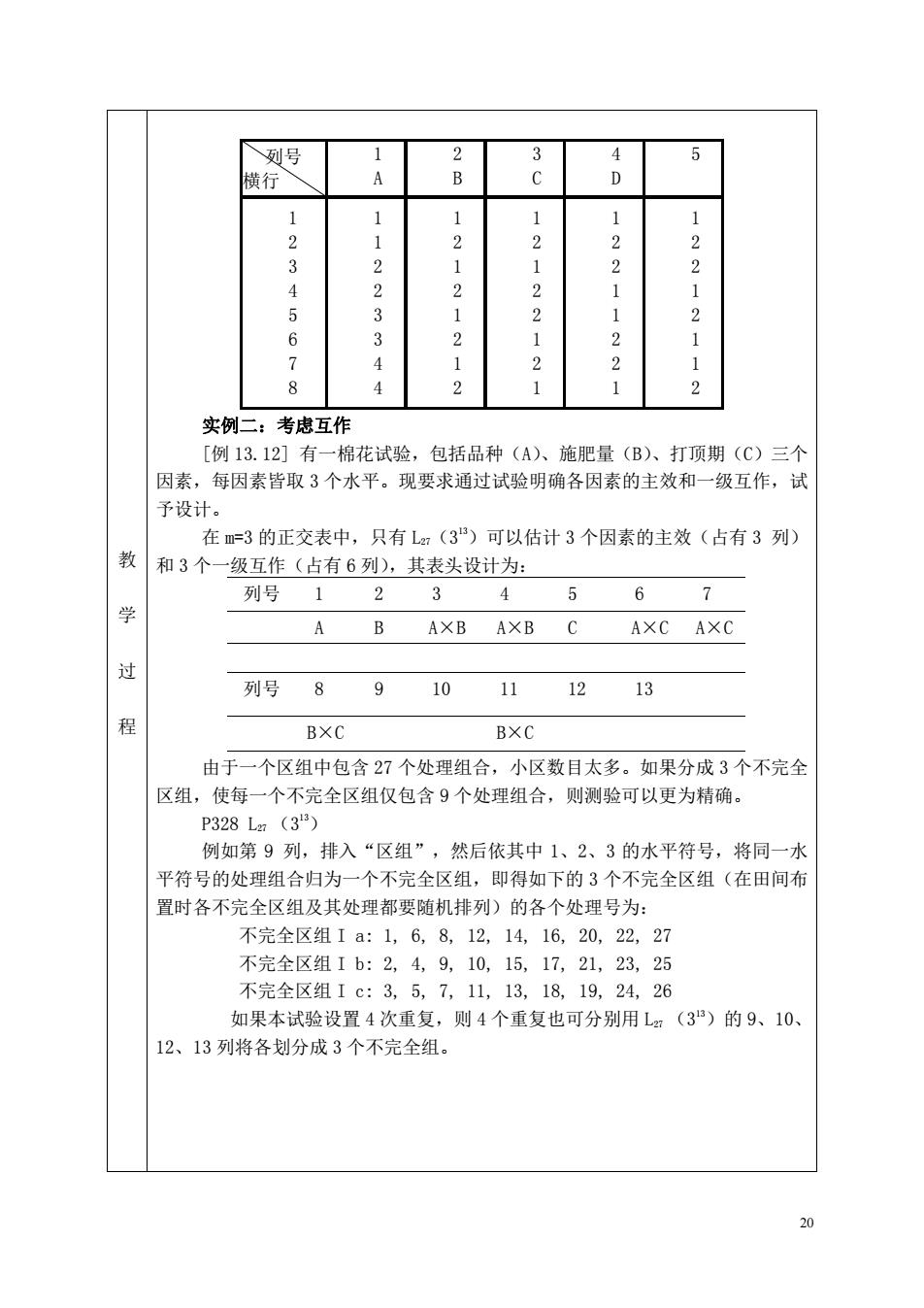
列号 2 3 5 行 B D 2 2 12 2 2 4 56 233 2 2 2 4 12 2 实例二:考虑互作 [例13.12]有一棉花试验,包括品种(A)、施肥量(B)、打顶期(C)三个 因素,每因素皆取3个水平。现要求通过试验明确各因素的主效和一级互作,试 予设计。 在m=3的正交表中,只有L:(3”)可以估计3个因素的主效(占有3列) 和3个一级互作(占有6列),其表头设计为: 列号 1 2 3 4 5 6 7 B AXBAXB AXC AXC 过 列号8 9 1011 1213 程 BXC BXC 由于一个区组中包含27个处理组合,小区数目太多。如果分成3个不完全 区组,使每一个不完全区组仅包含9个处理组合,则测验可以更为精确。 P328Lm(33) 例如第9列,排入“区组”,然后依其中1、2、3的水平符号,将同一水 平符号的处理组合归为一个不完全区组,即得如下的3个不完全区组(在田间布 置时各不完全区组及其处理都要随机排列)的各个处理号为: 不完全区组1a:1,6,8,12,14,16,20,22,27 不完全区组1b:2,4,9,10,15,17,21,23,25 不完全区组1c:3,5,7,11,13,18,19,24,26 如果本试验设置4次重复,则4个重复也可分别用Lm(3)的9、10、 12、13列将各划分成3个不完全组。 20
20 教 学 过 程 列号 横行 1 A 2 B 3 C 4 D 5 1 2 3 4 5 6 7 8 1 1 2 2 3 3 4 4 1 2 1 2 1 2 1 2 1 2 1 2 2 1 2 1 1 2 2 1 1 2 2 1 1 2 2 1 2 1 1 2 实例二:考虑互作 [例 13.12] 有一棉花试验,包括品种(A)、施肥量(B)、打顶期(C)三个 因素,每因素皆取 3 个水平。现要求通过试验明确各因素的主效和一级互作,试 予设计。 在 m=3 的正交表中,只有 L27(3 13)可以估计 3 个因素的主效(占有 3 列) 和 3 个一级互作(占有 6 列),其表头设计为: 列号 1 2 3 4 5 6 7 A B A×B A×B C A×C A×C 列号 8 9 10 11 12 13 B×C B×C 由于一个区组中包含 27 个处理组合,小区数目太多。如果分成 3 个不完全 区组,使每一个不完全区组仅包含 9 个处理组合,则测验可以更为精确。 P328 L27 (3 13) 例如第 9 列,排入“区组”,然后依其中 1、2、3 的水平符号,将同一水 平符号的处理组合归为一个不完全区组,即得如下的 3 个不完全区组(在田间布 置时各不完全区组及其处理都要随机排列)的各个处理号为: 不完全区组 I a: 1, 6, 8, 12, 14, 16, 20, 22, 27 不完全区组 I b: 2, 4, 9, 10, 15, 17, 21, 23, 25 不完全区组 I c: 3, 5, 7, 11, 13, 18, 19, 24, 26 如果本试验设置 4 次重复,则 4 个重复也可分别用 L27 (3 13)的 9、10、 12、13 列将各划分成 3 个不完全组