
再定义,增益函数:G(o)=10log1oT(jo) 2010g10T(j@) 因此: A(ω)=-G(ω) 衰减函数 增益函数 《网综》UESTC一陈会主讲
再定义,增益函数: 20log ( ) ( ) 10log ( ) 1 0 2 1 0 T j G T j 因此: A() G() 衰减函数 增益函数 《网综》UESTC—陈会主讲

又: r(j)=In H(jo)=InH(ja)eH() =lnH(jw)+j∠H(jw)=(ω)+j8(o) a(@)=In H(j@) 单位:奈培 A(@)=20l0g H(j@) 单位:分贝 有:A(w)=8.6860x(ω) 对数l0g109 自然对数 《网综》UESTC一陈会主讲
又: ln ( ) ( ) ( ) ( ) ( ) ln ( ) ln ( ) ( ) H j j H j j r j H j H j e j H j ( ) 20log ( ) ( ) ln ( ) A H j H j 单位:奈培 单位:分贝 有: A() 8.686() 对数log10。 自然对数 《网综》UESTC—陈会主讲

相位有: ∠H(jo)=-∠T(jω) 令: ∠T(j⊙)=(o) 群延迟可表达: d中(o) t()= dw A(o)=0,H(jo=1 没有衰减 定义一个关系: H(j@)2=1+K(j@)> 也可表达: K(j@)=H(j@)-1 《网综》UESTC一陈会主讲
相位有: H( j) T( j) 令: T( j) () d d ( ) 群延迟可表达: ( ) 定义一个关系: A() 0, H( j) 1 没有衰减 2 2 H( j) 1 K( j) 也可表达: ( ) ( ) 1 2 2 K j H j 《网综》UESTC—陈会主讲

特征函数 K(S |H(jω)2=1+K(jw)f K(jo)=H(j@)-1 可以导出衰减函数和特征函数的关系: A(ω)=101og1o[1+K(jw)] 衰减函数 特征函数 《网综》UESTC-一陈会主讲
特征函数 K(s) 2 2 H( j) 1 K( j) ( ) ( ) 1 2 2 K j H j 可以导出衰减函数和特征函数的关系: ( ) 10log [1 ( ) ] 2 A 1 0 K j 衰减函数 特征函数 《网综》UESTC—陈会主讲
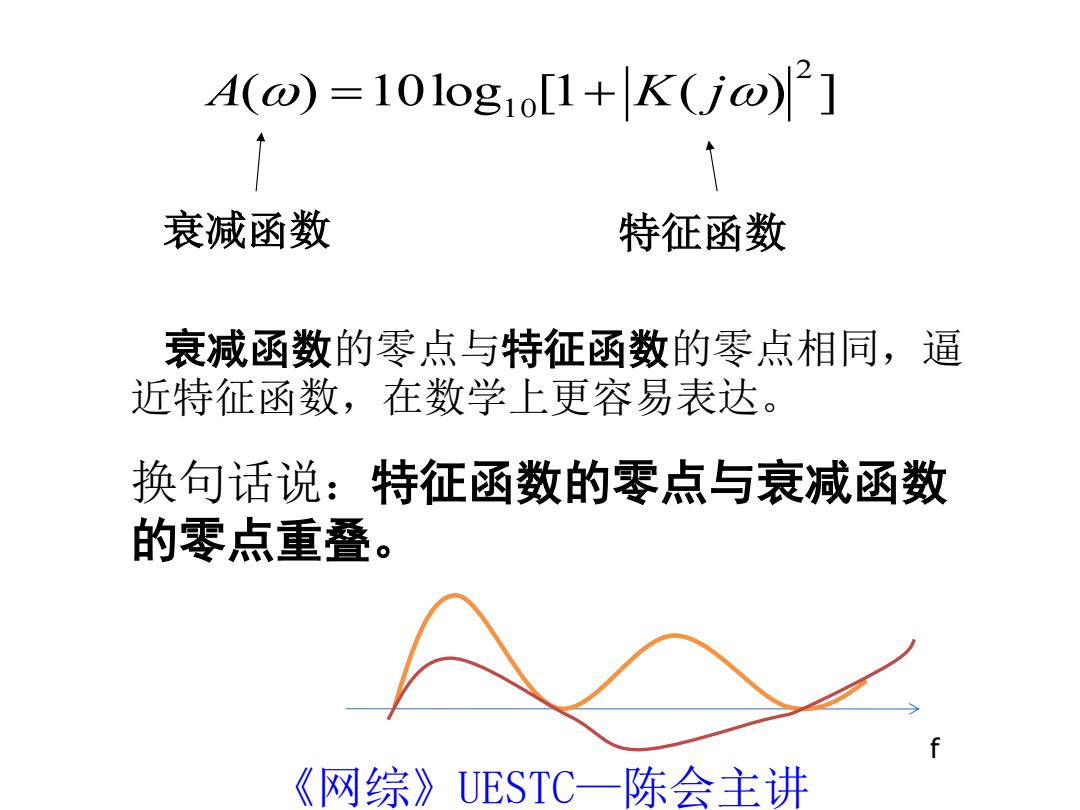
4( D)=10log1o[1+K(jo)2] 衰减函数 特征函数 衰减函数的零点与特征函数的零点相同,逼 近特征函数,在数学上更容易表达。 换句话说:特征函数的零点与衰减函数 的零点重叠。 《网综》UESTC一陈会主讲
衰减函数的零点与特征函数的零点相同,逼 近特征函数,在数学上更容易表达。 换句话说:特征函数的零点与衰减函数 的零点重叠。 ( ) 10log [1 ( ) ] 2 A 1 0 K j 衰减函数 特征函数 f 《网综》UESTC—陈会主讲