
二、四格表资料X检验 的连续性校正 应用校正公式条件 在四格表资料中,当n>40且某一个理论数 1≤T<5时。 x2= ∑01-1-0.5} T x2= (ad -be-n/2)n (a+b)c+dya+c)b+d) 13
13 二、四格表资料X 2检验 的连续性校正 应用校正公式条件 在四格表资料中,当n≥40且某一个理论数 1≤T<5时。 ( ) ( ) (a b)(c d )(a c)(b d ) ad bc n n x T A T x + + + + − − = − − = 2 2 2 2 / 2 0.5
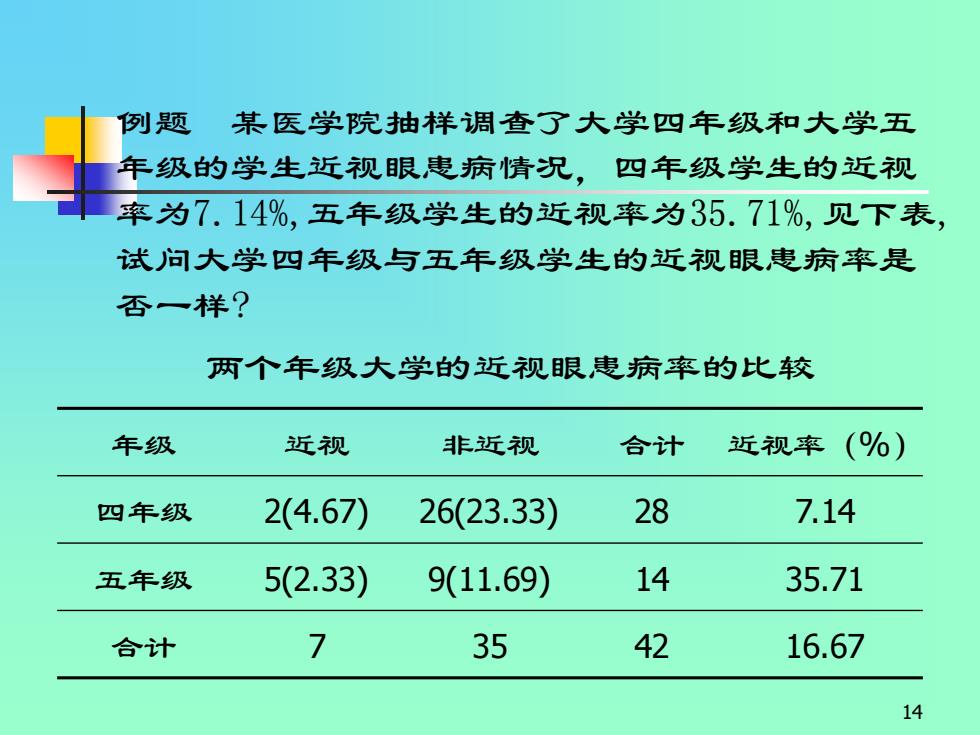
例题 某医学院抽样调查了大学四年级和大学五 年级的学生近视眼患病情况,四年级学生的近视 率为7.14%,五年级学生的近视率为35.71%,见下表, 试问大学四年级与五年级学生的近视眼患病率是 否一样? 两个年级大学的近视眼患病率的比较 年级 近视 非近视 合计 近视率(%) 四年级 2(4.67) 26(23.33) 28 7.14 五年级 5(2.33) 9(11.69) 14 35.71 合计 7 35 42 16.67 14
14 例题 某医学院抽样调查了大学四年级和大学五 年级的学生近视眼患病情况,四年级学生的近视 率为7.14%,五年级学生的近视率为35.71%,见下表, 试问大学四年级与五年级学生的近视眼患病率是 否一样? 年级 近视 非近视 合计 近视率(%) 四年级 2(4.67) 26(23.33) 28 7.14 五年级 5(2.33) 9(11.69) 14 35.71 合计 7 35 42 16.67 两个年级大学的近视眼患病率的比较

建立检验假设,确定检验水准 Ho: 四年级与五年级学生的近视眼患病率相同 兀1=元2 H:四年级与五年级学生的近视眼患病率不相同 元1丰兀2 =0.05 2、计算统计量x2 因为有两个理论频数小于己于5,但大于1,n=42>40 故用校正公式 15
15 1、建立检验假设,确定检验水准 H0:四年级与五年级学生的近视眼患病率相同 π1 = π2 H1:四年级与五年级学生的近视眼患病率不相同 π1 ≠ π2 α= 0.05 2、计算统计量x 2 因为有两个理论频数小于己于5,但大于1,n=42>40 故用校正公式

2 26 28 5 9 14 7 35 42 x2 (ad -be-n/2)"n (a+b)c+dya+c)b+d) 2x9-20x5-3 ×42 (2+262+55+926+9) =3.62 16
16 ( ) ( )( )( )( ) ( )( )( )( ) 3.62 2 26 2 5 5 9 26 9 42 2 42 2 9 26 5 / 2 2 2 2 = + + + + − − = + + + + − − = a b c d a c b d ad bc n n x 2 26 28 5 9 14 7 35 42

3、确定P值和判断结果 v=(2-1)(2-1)=1查x2界值表 X0.051)=3.84>x2=3.62,得P>0.05 按=0.05水准接受H,说明四年级与 五年的学生近视眼患病率差别没有统 计学意义. 17
17 3、确定P值和判断结果 ν=(2-1)(2-1)=1 查x 2界值表 X 2 0.05(1)=3.84 > x2=3.62,得P > 0.05 按α=0.05水准接受H0,说明四年级与 五年的学生近视眼患病率差别没有统 计学意义