
扩展域GF(2m)中的加法 0 在GF(2m中,将每个非0元素用多项式ax)表示,其系数至少 有一个不为0。对于=0,1,2,,2m-2,有: a1=a(☒)=a,0+a,X+a,2x2+..+a,m-1xm-1 ·考虑m=3,有限域表示为GF(23),下表为上式描述的基本元素 {x,xl,x2映射为7个元素{a和一个0元素。表中的各行是二进 制数字序列,代表上式中的系数a,0、a、a2的取值。 2013/4/11 12
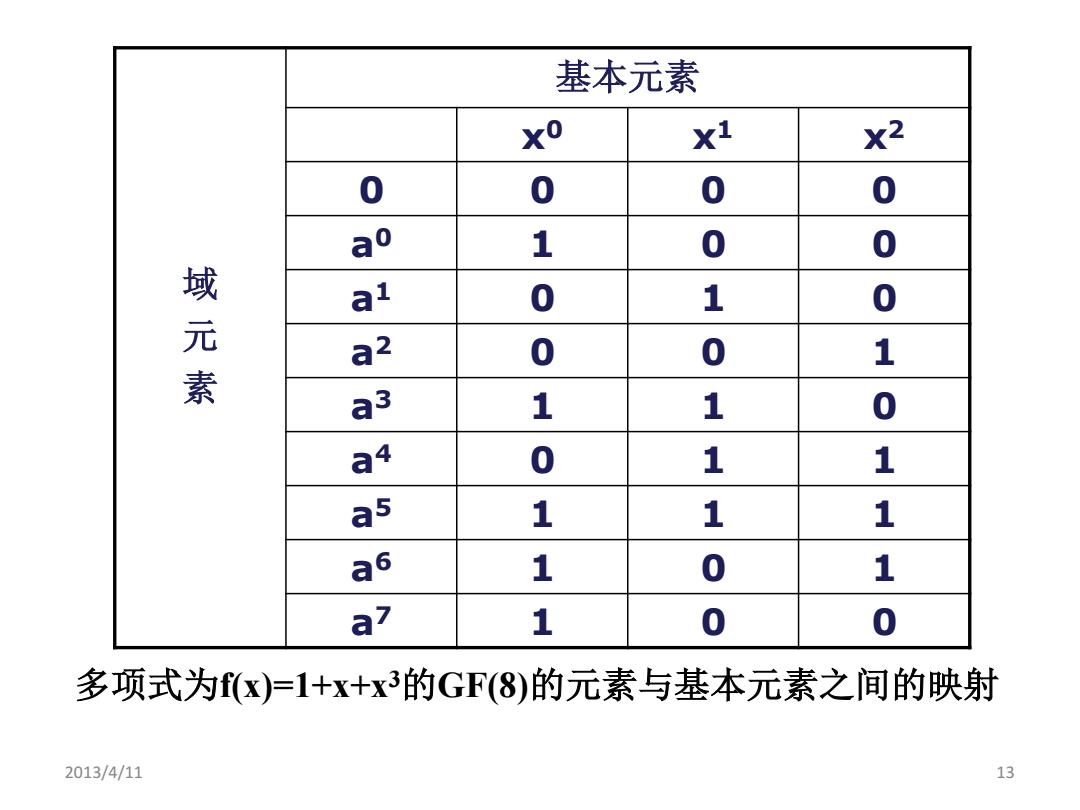
2013/4/11 12 扩展域GF(2m)中的加法 • 在GF(2m)中,将每个非0元素用多项式ai (x)表示,其系数至少 有一个不为0。对于i=0,1, 2,…,2m-2,有: ai = ai (x) = ai,0+ai,1x+ai,2x2+…+ai,m-1xm-1 • 考虑m=3,有限域表示为GF(23),下表为上式描述的基本元素 {x0,x1,x2}映射为7个元素{ai }和一个0元素。表中的各行是二进 制数字序列,代表上式中的系数ai,0、ai,1、ai,2的取值
基本元素 xO xi x2 0 0 0 0 ao 1 0 0 域元素 al 0 1 0 a2 0 0 1 a3 1 1 0 a4 0 1 1 as 1 1 1 a6 1 0 1 a7 1 0 0 多项式为f(x)=1+x+x3的GF(8)的元素与基本元素之间的映射 2013/4/11 13
2013/4/11 13 域 元 素 基本元素 x0 x1 x2 0 0 0 0 a0 1 0 0 a1 0 1 0 a2 0 0 1 a3 1 1 0 a4 0 1 1 a5 1 1 1 a6 1 0 1 a7 1 0 0 多项式为f(x)=1+x+x3的GF(8)的元素与基本元素之间的映射

·有限域中两个元素的加法定义为两个多项式中同幂次项系数 进行模2加,即 aiai=(aioajo)(aiIaj..+(ai.m-I+ai.m-1)xm-I ·有限域的本原多项式:因为这些函数用来定义有限域GF(2m)。 一个多项式是本原多项式的充要条件:一个阶的不可约多项 式fx),如果f(x)整除x+1的最小正整数n满足n=2m-1,则该多 项式是本原的。 例3.3本原多项式的辨别 (1)p(x)=1+x+x4 (2)p2(x)=1+x+x2+x3+x4 分析:(1)通过验证这个幂次为m=4的多项式是否能够整除x+1,但不能整 除1≤n<15范围内的x+1,就可以确定它是否为本原多项式。经反复计算, P1()是本原多项式,p2(x)不是,因为它能整除x5+1。 2013/4/11 14
2013/4/11 14 • 有限域中两个元素的加法定义为两个多项式中同幂次项系数 进行模2加,即 ai +aj =(ai,0+aj,0)+ (ai,1+aj,1)x+… +(ai,m-1+aj,m-1)xm-1 • 有限域的本原多项式:因为这些函数用来定义有限域GF(2m)。 一个多项式是本原多项式的充要条件:一个m阶的不可约多项 式f(x),如果f(x)整除xn+1的最小正整数n满足n=2m-1,则该多 项式是本原的。 • 例3.3 本原多项式的辨别 (1) p1(x)=1+x+x4 (2) p2(x)=1+x+x2+x3+x4 分析: (1)通过验证这个幂次为m=4的多项式是否能够整除 xn+1,但不能整 除1≤n<15范围内的xn+1,就可以确定它是否为本原多项式。经反复计算, p1(x)是本原多项式,p2(x)不是,因为它能整除x5+1

部分本原多项式 m m 3 1+x+x3 11 1+x2+x11 4 1+X+x4 12 1+X+x4+x6+x12 5 1+x2+x5 13 1+×+x3+x4+x13 6 1+X+x6 14 1+×+x6+x10+x14 7 1+x3+x7 15 1+X+x15 8 1+x2+x3+X4+x8 16 1+X+x3+x12+x16 9 1+x4+x9 17 1+x3+x17 10 1+x3+x10 18 1+x7+x18 2013/4/11 15
2013/4/11 15 部分本原多项式 m m 3 1+x+x3 11 1+x2+x11 4 1+x+x4 12 1+x+x4+x6+x12 5 1+x2+x5 13 1+x+x3+x4+x13 6 1+x+x6 14 1+x+x6+x10+x14 7 1+x3+x7 15 1+x+x15 8 1+x2+x3+x4+x8 16 1+x+x3+x12+x16 9 1+x4+x9 17 1+x3+x17 10 1+x3+x10 18 1+x7+x18

考虑一个本原多项式定义的有限域的例子 ·选择p(x)=1+x+x3,多项式的幂次为m=3,所以由px)所定义 的域中包含了2m=23=8个元素。求解p(x)的根就是指找到x 使p(x)=0。我们所熟悉的二进制数0和1不能满足,因为 p(I)=1,p(0)=1(运用模2运算)。由基本代数学理论我们知 道,对于幂次为m的多项式必然有m个根。对于这个例子, p(x)=0有3个根,由于这3个根不可能位于与p(x)系数相同 的有限域中,而是位于扩展域GF(2)中。用扩展域的元素 a来定义多项式p(x)的根,可写成如下形式:p(a=0 2013/4/11 16
2013/4/11 16 考虑一个本原多项式定义的有限域的例子 • 选择p(x)=1+x+x3 ,多项式的幂次为m=3,所以由p(x)所定义 的域中包含了2m=23=8个元素。求解p(x)的根就是指找到x 使p(x)=0。我们所熟悉的二进制数0和1不能满足,因为 p(1)=1,p(0)=1 (运用模2运算)。由基本代数学理论我们知 道,对于幂次为m的多项式必然有m个根。对于这个例子, p(x)=0有3个根,由于这3个根不可能位于与p(x)系数相同 的有限域中,而是位于扩展域GF(23)中。用扩展域的元素 a来定义多项式p(x)的根,可写成如下形式:p(a)=0