
块 ■对于阶至少为3的连通图G 1.G没有割点。 →2.对于任意两个顶点,v∈V,G含两条无公共内顶点的路。 ■采用数学归纳法,对两个顶点间的距离归纳。 ●当dis(uv)=1时,为什么成立? -G没有割点→没有割边→和v共圈 ●假设dis(u,v)=k时成立,则dis(u,v)=k+1时 -dis(u,w)=k→共圈 一若这个圈经过? u 2023/3/20 26
n 对于阶至少为3的连通图G 1. G没有割点。 2. 对于任意两个顶点u, v ∈ V ,G含两条无公共内顶点的u-v路。 n 采用数学归纳法,对两个顶点间的距离归纳。 l 当dist(u, v) = 1时,为什么成立? – G没有割点 à 没有割边 à u和v共圈 l 假设dist(u, v) = k时成立,则dist(u, v) = k + 1时 – dist(u, w) = k à 共圈 – 若这个圈经过v? 2023/3/20 26 块 u w P v Q
块 ■对于阶至少为3的连通图G 1.G没有割点。 ◆2. 对于任意两个顶点u,v∈V',G含两条无公共内顶点的-v路。 ■采用数学归纳法,对两个顶点间的距离归纳。 ●当dis(u,v)=1时,为什么成立? -G没有割点→没有割边→和v共圈 ●假设dis(u,v)=k时成立,则dis(u,v)=k+1时 -is(u,w)=k→共圈 一不经过的路与上述圈有公共顶点怎么办? u W ----2222----- 2023/3/20 27
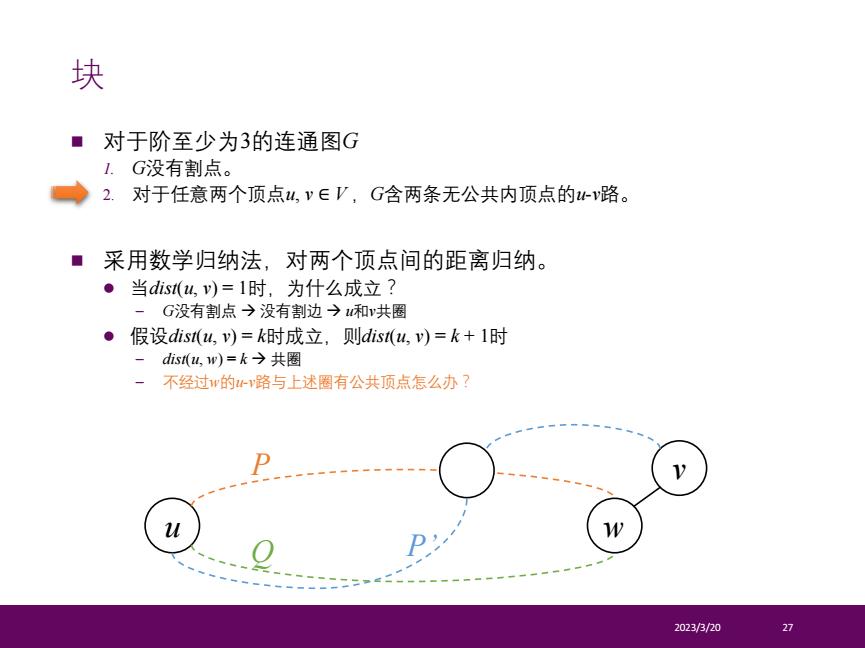
n 对于阶至少为3的连通图G 1. G没有割点。 2. 对于任意两个顶点u, v ∈ V ,G含两条无公共内顶点的u-v路。 n 采用数学归纳法,对两个顶点间的距离归纳。 l 当dist(u, v) = 1时,为什么成立? – G没有割点 à 没有割边 à u和v共圈 l 假设dist(u, v) = k时成立,则dist(u, v) = k + 1时 – dist(u, w) = k à 共圈 – 不经过w的u-v路与上述圈有公共顶点怎么办? 2023/3/20 27 块 u w P v Q P’
块 ■对于阶至少为3的连通图G 1.G没有割点。 →2.对于任意两个顶点,v∈V,G含两条无公共内顶点的路。 ■采用数学归纳法,对两个顶点间的距离归纳。 ·当dis(u,v)=1时,为什么成立? -G没有割点→没有割边→和v共圈 ●假设dis(u,v)=k时成立,则dist(uv)=k+1时 -dis(u,p)=k→共圈 -x:不经过w的路与上述圈的最后一个公共顶点 1) u 2023/3/20 28
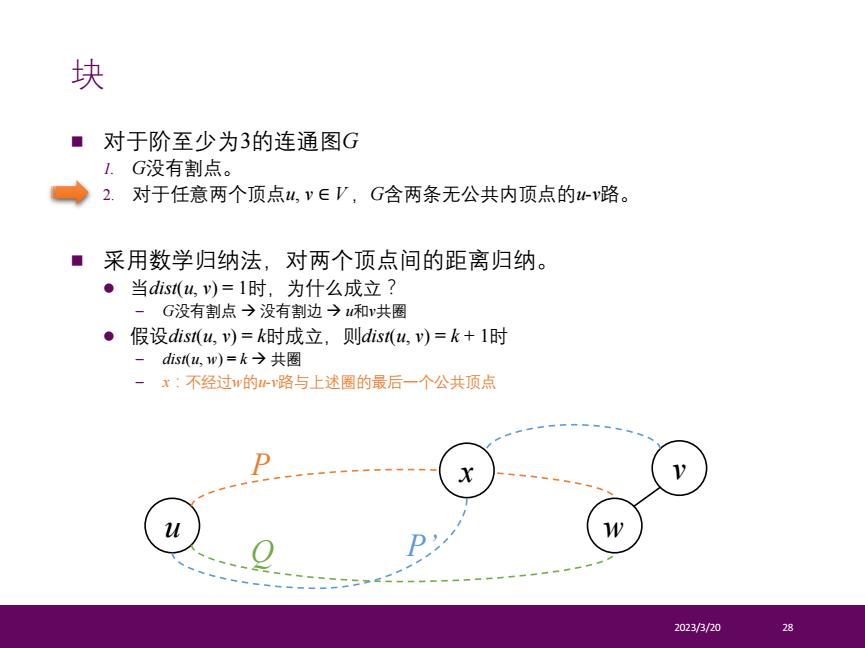
n 对于阶至少为3的连通图G 1. G没有割点。 2. 对于任意两个顶点u, v ∈ V ,G含两条无公共内顶点的u-v路。 n 采用数学归纳法,对两个顶点间的距离归纳。 l 当dist(u, v) = 1时,为什么成立? – G没有割点 à 没有割边 à u和v共圈 l 假设dist(u, v) = k时成立,则dist(u, v) = k + 1时 – dist(u, w) = k à 共圈 – x:不经过w的u-v路与上述圈的最后一个公共顶点 2023/3/20 28 块 u w P v Q x P’
块 ■对于阶至少为3的连通图G 1.G没有割点。 ◆2. 对于任意两个顶点u,v∈V',G含两条无公共内顶点的-v路。 ■采用数学归纳法,对两个顶点间的距离归纳。 ●当dis(u,v)=1时,为什么成立? -G没有割点→没有割边→和v共圈 ●假设dis(u,)=k时成立,则dist(u,v)=k+1时 -di(u,p)=k→共圈 -x:不经过的路与上述圈的最后一个公共顶点 两条无公共内顶点的路:P中的-x路拼接P中的x-v路,Q拼接(w,) W D 2023/3/20 29
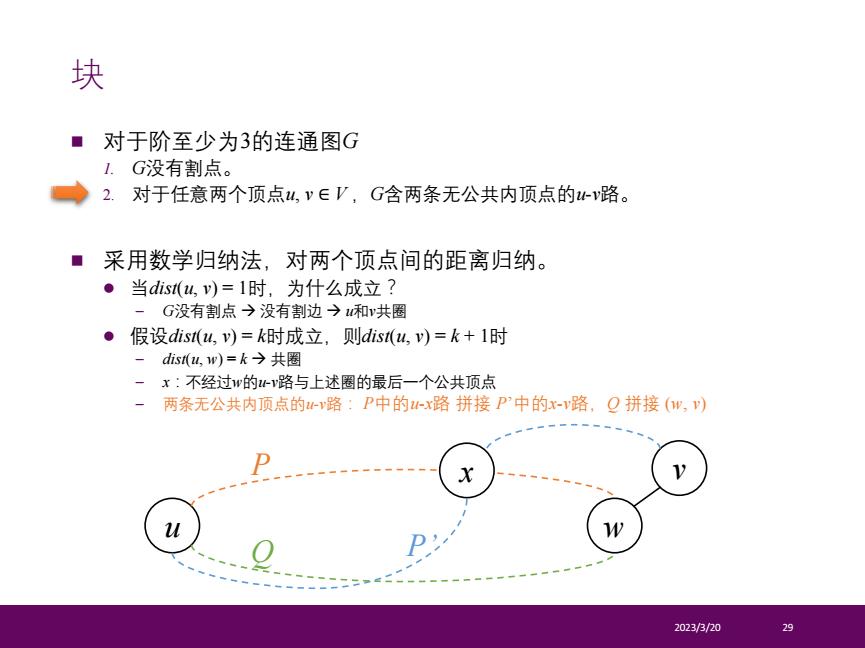
n 对于阶至少为3的连通图G 1. G没有割点。 2. 对于任意两个顶点u, v ∈ V ,G含两条无公共内顶点的u-v路。 n 采用数学归纳法,对两个顶点间的距离归纳。 l 当dist(u, v) = 1时,为什么成立? – G没有割点 à 没有割边 à u和v共圈 l 假设dist(u, v) = k时成立,则dist(u, v) = k + 1时 – dist(u, w) = k à 共圈 – x:不经过w的u-v路与上述圈的最后一个公共顶点 – 两条无公共内顶点的u-v路: P中的u-x路 拼接 P’中的x-v路,Q 拼接 (w, v) 2023/3/20 29 块 u w P v Q x P’

块 ■对于阶至少为3的连通图G →1G没有割点。 2.对于任意两个顶点w,v∈V,G含两条无公共内顶点的v路。 ■你能自己证明吗? 2023/3/20 30
n 对于阶至少为3的连通图G 1. G没有割点。 2. 对于任意两个顶点u, v ∈ V ,G含两条无公共内顶点的u-v路。 n 你能自己证明吗? 2023/3/20 30 块