
第1章绪论 人。接下来,进一步阐述了国内外学者针对混合驱动机构的研究现状,包括研究 内容以及所取得成果等。本章末尾给出了本论文的主要内容和结构安排。 第二章为平面闭链连杆机构的构型综合,首先分析单自出度连杆机构与两自 由度连杆机构的构型综合,并且给出了各种类型的缩图形式和结构简图。通过连 杆机构的构型综合,在两自由度机构中推导出了混合驱动机构的标准模型一混合 驱动五杆机构,在单自由度机构中推导出了具有复式闭链的斯蒂芬逊机构以及由 此演化得到的某个连杆长度可调节的混合驱动七杆机构。接着,本章分析了平面 四杆机构和混合驱动五杆机构的机构分类,重点对混合驱动七杆机构进行了结构 分析。 第三章为混合驱动五杆机构的相关分析与实验研究,首先分析五杆机构的工 作空间,得到了末端执行器位于工作空间边界的条件。接着进行五杆机构的运动 学分析,通过列写机构的封闭矢量方程式,己知驱动杆件的运动规律能够得到从 动杆件的位移、速度和加速度:已知末端执行器的运动轨迹能够推导出伺服电机 的变化规律。利用拉格朗日方程建立五杆机构的动力学模型,并且在ADAMS 中构建虚拟样机模型,进行了仿真分析。本章重点分析了两种轨迹规划方法,分 别基于逆运动学分析和基于轨迹曲线簇,在混合驱动五杆机构实验平台上进行了 相关实验。 第四章为混合驱动型四足机器人腿部机构的分析与研究,首先介绍机器人腿 部机构模型与七杆机构尺度优化过程。接着进行七杆机构的工作空间分析,推导 出杆c长度的变化范围,通过七杆机构末端点处于工作空间边界的条件得到了工 作空间的边界曲线。利用雅可比矩阵对七杆机构的速度特性进行了分析,比较了 尺寸参数、调节参数和控制参数对速度特性的影响。电机的动力特性直接整体机 构的运动精度,在七杆机构的动力学分析过程中引入了电机环节,进行了机电耦 合建模与仿真。特定轨迹实现采用的是基于轨迹曲线簇的近似求解方法,在机器 人腿部机构实验平台上进行了四种不同轨迹的实验。 第五章为总结与展望,对全文的研究工作和主要结论进行了总结,并对下一 步的深入研究进行了展望。 10
第1章绪论 人。接下来,进一步阐述了国内外学者针对混合驱动机构的研究现状,包括研究 内容以及所取得成果等。本章末尾给出了本论文的主要内容和结构安排。 第二章为平面闭链连杆机构的构型综合,首先分析单自由度连杆机构与两自 由度连杆机构的构型综合,并且给出了各种类型的缩图形式和结构简图。通过连 杆机构的构型综合,在两自由度机构中推导出了混合驱动机构的标准模型一混合 驱动五杆机构,在单自由度机构中推导出了具有复式闭链的斯蒂芬逊机构以及由 此演化得到的某个连杆长度可调节的混合驱动七杆机构。接着,本章分析了平面 四杆机构和混合驱动五杆机构的机构分类,重点对混合驱动七杆机构进行了结构 分析。 第三章为混合驱动五杆机构的相关分析与实验研究,首先分析五杆机构的工 作空间,得到了末端执行器位于工作空间边界的条件。接着进行五杆机构的运动 学分析,通过列写机构的封闭矢量方程式,己知驱动杆件的运动规律能够得到从 动杆件的位移、速度和加速度;已知末端执行器的运动轨迹能够推导出伺服电机 的变化规律。利用拉格朗日方程建立五杆机构的动力学模型,并且在ADAMS 中构建虚拟样机模型,进行了仿真分析。本章重点分析了两种轨迹规划方法,分 别基于逆运动学分析和基于轨迹曲线簇,在混合驱动五杆机构实验平台上进行了 相关实验。 第四章为混合驱动型四足机器人腿部机构的分析与研究,首先介绍机器人腿 部机构模型与七杆机构尺度优化过程。接着进行七杆机构的工作空间分析,推导 出杆c长度的变化范围,通过七杆机构末端点处于工作空间边界的条件得到了工 作空间的边界曲线。利用雅可比矩阵对七杆机构的速度特性进行了分析,比较了 尺寸参数、调节参数和控制参数对速度特性的影响。电机的动力特性直接整体机 构的运动精度,在七杆机构的动力学分析过程中引入了电机环节,进行了机电耦 合建模与仿真。特定轨迹实现采用的是基于轨迹曲线簇的近似求解方法,在机器 人腿部机构实验平台上进行了四种不同轨迹的实验。 第五章为总结与展望,对全文的研究工作和主要结论进行了总结,并对下一 步的深入研究进行了展望。 10

第2章平面闭链连杆机构的构型综合 第2章平面闭链连杆机构的构型综合 2.1平面连杆机构的基本概念 机构由许多构件组合而成,每个构件都以一定的方式与其他构件相互连接, 使得两个构件既能保持接触,又能产生相对运动。这样由两个构件直接接触形成 的相互连接称为运动副6)。构件之间的接触可以分为三种类型:点接触、线接触、 面接触,这些点、线、面称为运动副元素。互相啮合的轮齿之间的接触为点接触 或者线接触,滑块与导轨之间的接触为面接触。根据两个构件的接触特性,通常 把运动副分为高副和低副,点接触或者线接触的运动副称为高副,面接触的运动 副称为低副。按照运动副两个构件之间的相对运动是平面运动还是空间运动,可 以把运动副分为平面运动副和空间运动副两种类型。 运动链是由各种构件和运动副组成的完整约束系统。这个系统如果使运动链 的运动确定,或者是运动链的各种构件之间存在确定的相对运动,那么这个运动 链能够组成机构。如果组成运动链的各个构件构成了首尾封闭的系统,则称其为 闭式运动链,或者简称为闭链。如果组成运动链的各个构件并未构成首尾封闭的 系统,则称其为开式运动链,或者简称为开链。另外,根据运动链中各种构件之 间的相对运动是平面运动还是空间运动,同样可以把运动链分为平面运动链和空 间运动链两种类型。在连杆机构中一般采用的是平面闭式运动链,空间开式运动 链多应用于机械臂等场合。 如果将运动链中某个构件固定或者相对固定,这个构件称为机架,运动链被 称为机构,但是这个机构并不具有确定的运动。当机构中的一个或者几个构件具 有相对独立的运动,即是成为机构的原动件时,其余从动件的运动便可以确定, 整个机构的运动也就能够确定。具有确定运动的机构可以有效地传递运动和力。 依据形成机构的运动链是平面运动链还是空间运动链,也可把相应的机构分为平 面机构和空间机构两种类型。在实际场合中常用的机构大多数为平面机构。 在设计和分析机构时,一般都需要绘制该机构的运动简图。因为机构各个构 件之间的相对运动,通常只取决于机构中所有运动副的类型、数目以及相对位置 (例如旋转副的中心位置、移动副的中心线位置和高副的接触点位置等),与各 个构件的外形、零件数目和运动副具体结构无关。在分析机构的运动规律时,可 以不用考虑这些与运动规律无关的因素。机构运动简图用简单的线条和符号来表 示构件和运动副,并且按照一定的比例表示各个运动副之间的相对位置,如图 2.1所示。由于机构运动简图具有与原始机构完全相同的运动特性,因此可以根 11
第2章平面闭链连杆机构的构型综合 第2章平面闭链连杆机构的构型综合 2.1平面连杆机构的基本概念 机构由许多构件组合而成,每个构件都以一定的方式与其他构件相互连接, 使得两个构件既能保持接触,又能产生相对运动。这样由两个构件直接接触形成 的相互连接称为运动副【631。构件之间的接触可以分为三种类型:点接触、线接触、 面接触,这些点、线、面称为运动副元素。互相啮合的轮齿之间的接触为点接触 或者线接触,滑块与导轨之间的接触为面接触。根据两个构件的接触特性,通常 把运动副分为高副和低副,点接触或者线接触的运动副称为高副,面接触的运动 副称为低副。按照运动副两个构件之间的相对运动是平面运动还是空间运动,可 以把运动副分为平面运动副和空间运动副两种类型。 运动链是由各种构件和运动副组成的完整约束系统。这个系统如果使运动链 的运动确定,或者是运动链的各种构件之间存在确定的相对运动,那么这个运动 链能够组成机构。如果组成运动链的各个构件构成了首尾封闭的系统,则称其为 闭式运动链,或者简称为闭链。如果组成运动链的各个构件并未构成首尾封闭的 系统,则称其为开式运动链,或者简称为开链。另外,根据运动链中各种构件之 间的相对运动是平面运动还是空间运动,同样可以把运动链分为平面运动链和空 间运动链两种类型。在连杆机构中一般采用的是平面闭式运动链,空间开式运动 链多应用于机械臂等场合。 如果将运动链中某个构件固定或者相对固定,这个构件称为机架,运动链被 称为机构,但是这个机构并不具有确定的运动。当机构中的一个或者几个构件具 有相对独立的运动,即是成为机构的原动件时,其余从动件的运动便可以确定, 整个机构的运动也就能够确定。具有确定运动的机构可以有效地传递运动和力。 依据形成机构的运动链是平面运动链还是空间运动链,也可把相应的机构分为平 面机构和空间机构两种类型。在实际场合中常用的机构大多数为平面机构。 在设计和分析机构时,一般都需要绘制该机构的运动简图。因为机构各个构 件之间的相对运动,通常只取决于机构中所有运动副的类型、数目以及相对位置 (例如旋转副的中心位置、移动副的中心线位置和高副的接触点位置等),与各 个构件的外形、零件数目和运动副具体结构无关。在分析机构的运动规律时,可 以不用考虑这些与运动规律无关的因素。机构运动简图用简单的线条和符号来表 示构件和运动副,并且按照一定的比例表示各个运动副之间的相对位置,如图 2.1所示。由于机构运动简图具有与原始机构完全相同的运动特性,因此可以根 11

第2章平面闭链连杆机构的构型综合 据该图对机构进行运动学分析和动力学分析。机构运动简图可以不要求严格按照 比例关系来绘制,只是表示机构的结构情况,这样的机构运动简图称为机构示意 图,如图2.2所示。 77777777777 图2.1机构运动简图 图2.2机构示意图 2.2单自由度平面连杆机构的类型综合 机构是用来传递运动和力的系统,由具有确定运动规律的运动链组成。在设 计和分析机构时,首先应该判断这个机构能否运动。运动链的结构型式,例如构 件数目、各个构件之间的相对尺寸、运动副结构形式及其排列等都具有一定的内 在规律性。不满足这些规律会导致机构进行不确定的相对运动或者无法进行运 动。如果机构可以运动,还需要给出机构具有确定相对运动的条件。 在设计研制新机构时,约束条件往往是保证机构能够实现某种确定的运动规 律。但是由于构件数目和运动副形式的不同,机构的结构类型非常复杂。能够实 现确定运动的机构构件数目可能不同,在构件数目相同的情况下,实现确定运动 的结构类型也可能不止一种,因此在设计研制机构时有优化比较的必要。不同结 构类型的机构具有不同的运动学特性和动力学特性。根据机构组成学的相关知 识,通过对机构进行结构类型综合,可以得到各种不同类型的结构,进而为机构 设计研制提供各种参考方案[6466)。 广义上的机构类型综合是指机构设计过程中的选型,包括对凸轮、齿轮、连 杆等的选择。本章节所叙述的是狭义上的机构类型综合,只是针对平面连杆机构 的类型综合,它是指如何排列搭配构件和运动副以组成机构的过程。由于高副可 以用低副来替代,所以一般以运动副全部是旋转副的连杆机构为研究对象来进行 机构类型综合。 单自由度平面连杆机构如果解除机架的约束,将会得到一个自由度为4的运 动链。假设该运动链的构件数目为N,运动副数目为P,根据平面自由度方程推 12
第2章平面闭链连杆机构的构型综合 据该图对机构进行运动学分析和动力学分析。机构运动简图可以不要求严格按照 比例关系来绘制,只是表示机构的结构情况,这样的机构运动简图称为机构示意 图,如图2.2所示。 图2.1机构运动简图 2.2单自由度平面连杆机构的类型综合 图2.2机构示意图 机构是用来传递运动和力的系统,由具有确定运动规律的运动链组成。在设 计和分析机构时,首先应该判断这个机构能否运动。运动链的结构型式,例如构 件数目、各个构件之间的相对尺寸、运动副结构形式及其排列等都具有一定的内 在规律性。不满足这些规律会导致机构进行不确定的相对运动或者无法进行运 动。如果机构可以运动,还需要给出机构具有确定相对运动的条件。 在设计研制新机构时,约束条件往往是保证机构能够实现某种确定的运动规 律。但是由于构件数目和运动副形式的不同,机构的结构类型非常复杂。能够实 现确定运动的机构构件数目可能不同,在构件数目相同的情况下,实现确定运动 的结构类型也可能不止一种,因此在设计研制机构时有优化比较的必要。不同结 构类型的机构具有不同的运动学特性和动力学特性。根据机构组成学的相关知 识,通过对机构进行结构类型综合,可以得到各种不同类型的结构,进而为机构 设计研制提供各种参考方案畔枷】。 广义上的机构类型综合是指机构设计过程中的选型,包括对凸轮、齿轮、连 杆等的选择。本章节所叙述的是狭义上的机构类型综合,只是针对平面连杆机构 的类型综合,它是指如何排列搭配构件和运动副以组成机构的过程。由于高副可 以用低副来替代,所以一般以运动副全部是旋转副的连杆机构为研究对象来进行 机构类型综合。 单自由度平面连杆机构如果解除机架的约束,将会得到一个自由度为4的运 动链。假设该运动链的构件数目为Ⅳ,运动副数目为尸,根据平面自由度方程推 12

第2章平面闭链连杆机构的构型综合 导得到下列关系式: 3N-2P=4 (2.1) 另外,在N个构件中,假设具有i个运动副的构件数目为N,则有: ∑N=N (2.2) 在图论的相关知识中有这样一条定理:运动链拓扑图中所有顶点的度数等于 其边数的两倍。根据这个定理,可以得到以下关系式: ∑iN,=2P (2.3) 闭式运动链是一个封闭的几何图形,即构成一个闭环回路。图论中的欧拉定 理可以用来分析运动链的结构。欧拉定理表述如下:个简单闭环回路中存在V 个顶、E条边组成的一个多边形网络,应该满足下式: V-E+L=1 (2.4) 根据运动链拓扑图中对顶和边的定义:顶是一个点,代表运动链的构件:边 是一条线段,代表运动链的运动副。于是,欧拉定理中的顶数V、边数E和回路 数L可以用运动链中的构件数目N、运动副数目P和闭链数目1来替代。(2.4) 式可转换为: P-N+1=l (2.5) 本节讨论的只是单自由度平面连杆机构,将(2.1)式代入到(2.5)式中, 消去其中的N,最终得到: P-31=1 (2.6) 满足(2.1)式和(2.6)式的运动链有很多,根据构件数目的递增可以得到 如表2.1所示的运动链排列方式。 表21不同构件数目N组成的运动链 构件数目N 运动副数目P 闭链数目1 1 1 0 1 6 7 2 10 3 10 13 4 由上表可知,=2的平面连杆机构闭链数目为0,因此该机构为开式运动链, 如图2.3所示。N=4的平面连杆机构闭链数目为1,运动副数目为4,该机构的 运动链只存在一种结构型式,就是常用的四杆机构,如图2.4所示。N=6的平面 连杆机构闭链数目为2,运动副数目为7,该机构的运动链存在两种不同的结构 型式,如图2.5所示,(a)为瓦特机构,(b)为斯蒂芬逊机构。N=8的平面连杆 13
第2章平面闭链连杆机构的构型综合 导得到下列关系式: 3N一2P=4 (2.1) 另外,在Ⅳ个构件中,假设具有i个运动副的构件数目为M,则有: ∑N/=N (2.2) 在图论的相关知识中有这样一条定理:运动链拓扑图中所有顶点的度数等于 其边数的两倍。根据这个定理,可以得到以下关系式: ∑以=2P (2.3) 闭式运动链是一个封闭的几何图形,即构成一个闭环回路。图论中的欧拉定 理可以用来分析运动链的结构。欧拉定理表述如下:三个简单闭环回路中存在矿 个顶、E条边组成的一个多边形网络,应该满足下式: y—E+L=1 (2.4) 根据运动链拓扑图中对顶和边的定义:顶是一个点,代表运动链的构件;边 是一条线段,代表运动链的运动副。于是,欧拉定理中的顶数玖边数E和回路 数三可以用运动链中的构件数目N、运动副数目尸和闭链数目Z来替代。(2.4) 式可转换为: 尸一Ⅳ+1=, (2.5) 本节讨论的只是单自由度平面连杆机构,将(2.1)式代入到(2.5)式中, 消去其中的Ⅳ,最终得到: 尸一3l=1 (2.6) 满足(2.1)式和(2.6)式的运动链有很多,根据构件数目的递增可以得到 如表2.1所示的运动链排列方式。 表2.1不同构件数目Ⅳ组成的运动链 构件数目N 运动副数目P 闭链数目, 2 1 0 4 4 1 6 7 2 8 10 3 10 13 4 由上表可知,N=2的平面连杆机构闭链数目为0,因此该机构为开式运动链, 如图2.3所示。N=4的平面连杆机构闭链数目为1,运动副数目为4,该机构的 运动链只存在一种结构型式,就是常用的四杆机构,如图2.4所示。N=6的平面 连杆机构闭链数目为2,运动副数目为7,该机构的运动链存在两种不同的结构 型式,如图2.5所示,(a)为瓦特机构,(b)为斯蒂芬逊机构。N=8的平面连杆 13
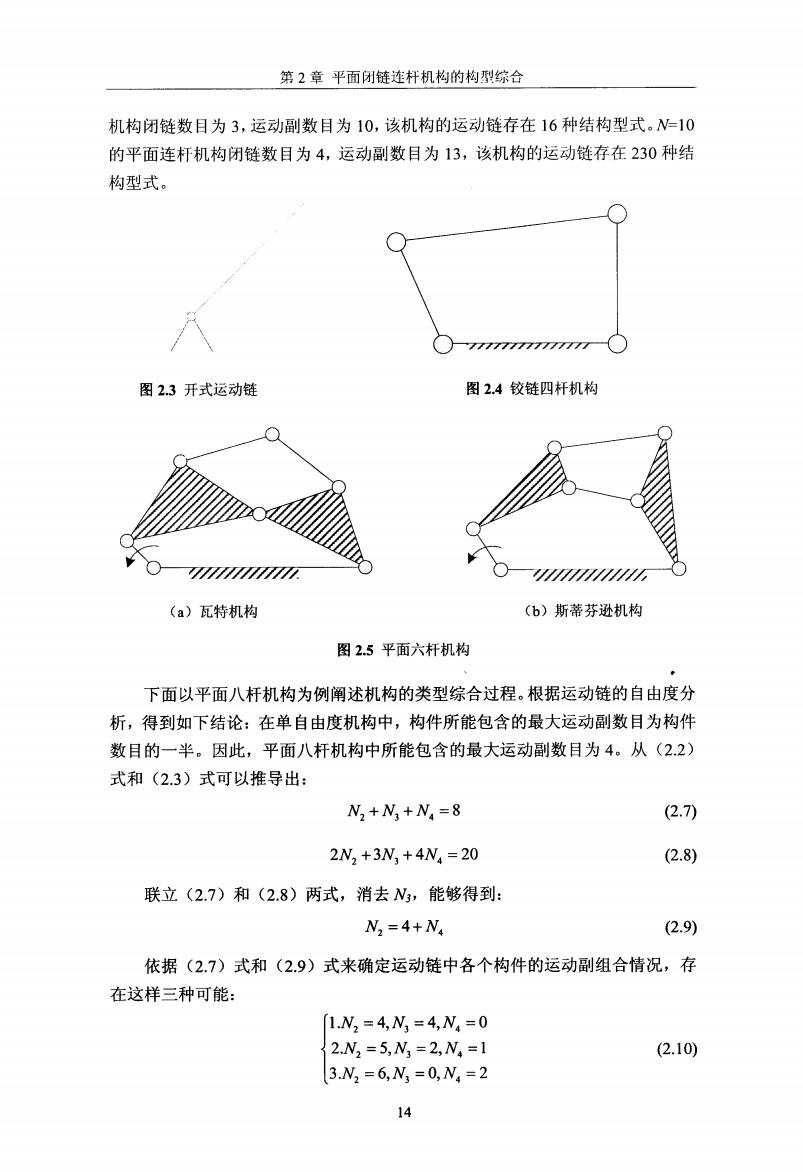
第2章平面闭链连杆机构的构型综合 机构闭链数目为3,运动副数目为10,该机构的运动链存在16种结构型式。W=10 的平面连杆机构闭链数目为4,运动副数目为13,该机构的运动链存在230种结 构型式。 777777777777777 图2.3开式运动链 图2.4铰链四杆机构 (a)瓦特机构 (b)斯蒂芬逊机构 图2.5平面六杆机构 下面以平面八杆机构为例阐述机构的类型综合过程。根据运动链的自由度分 析,得到如下结论:在单自由度机构中,构件所能包含的最大运动副数目为构件 数目的一半。因此,平面八杆机构中所能包含的最大运动副数目为4。从(2.2) 式和(23)式可以推导出: N2+N3+N,=8 (2.7) 2N,+3N,+4N4=20 (2.8) 联立(2.7)和(2.8)两式,消去N3,能够得到: N2=4+N4 (2.9) 依据(2.7)式和(2.9)式来确定运动链中各个构件的运动副组合情况,存 在这样三种可能: 1.N2=4,N3=4,N4=0 2N2=5,N3=2,N4=1 (2.10) 3.N2=6,N3=0,N4=2 14
第2章平面闭链连杆机构的构型综合 机构闭链数目为3,运动昌0数目为10,该机构的运动链存在16种结构型式。N=10 的平面连杆机构闭链数目为4,运动副数目为13,该机构的运动链存在230种结 构型式。 图2.3开式运动链 (a)瓦特机构 图2.4铰链四杆机构 (b)斯蒂芬逊机构 图2.5平面六杆机构 、 ● 下面以平面八杆机构为例阐述机构的类型综合过程。根据运动链的自由度分 析,得到如下结论:在单自由度机构中,构件所能包含的最大运动副数目为构件 数目的一半。因此,平面八杆机构中所能包含的最大运动副数目为4。从(2.2) 式和(2.3)式可以推导出: Ⅳ2+Ⅳ3+Ⅳ4=8 (2.7) 2N2+3Ⅳ3+4N4=20 (2.8) 联立(2.7)和(2.8)两式,消去M,能够得到: Ⅳ2=4+Ⅳ4 (2.9) 依据(2.7)式和(2.9)式来确定运动链中各个构件的运动副组合情况,存 在这样三种可能: 11.Ⅳ2=4,Ⅳ3=4,N4=0 {2.N2=5,Ⅳ3=2,Ⅳ4=1 (2.10) 【3.N2=6,Ⅳ3=o,Ⅳ4=2 14