
2.1数据通信的理论基础 2.1.1 Fourier级数 任何正常的周期为T的函数g()都可以展开成 Fourier级数,即 g(t)= 2c+∑a,sin2ni))+2h,cos2ufm n=l n=l f=1/T:基频 anb: n次谐波(Harmonics)Fourier分量的正 弦和余弦振幅 gt0snm2xn0h&-子g0eas2=子gto0d 0=1
2.1数据通信的理论基础 ◼ 2.1.1 Fourier 级数 ◼ 任何正常的周期为T的函数g(t)都可以展开成 Fourier级数,即 :基频 :n次谐波(Harmonics)/Fourier分量的正 弦和余弦振幅 f T =1/ , n n a b 0 2 ( )sin(2 ) T n a g t nft dt T = 0 2 ( )cos(2 ) T n b g t nft dt T = 0 2 ( ) T c g t dt T =
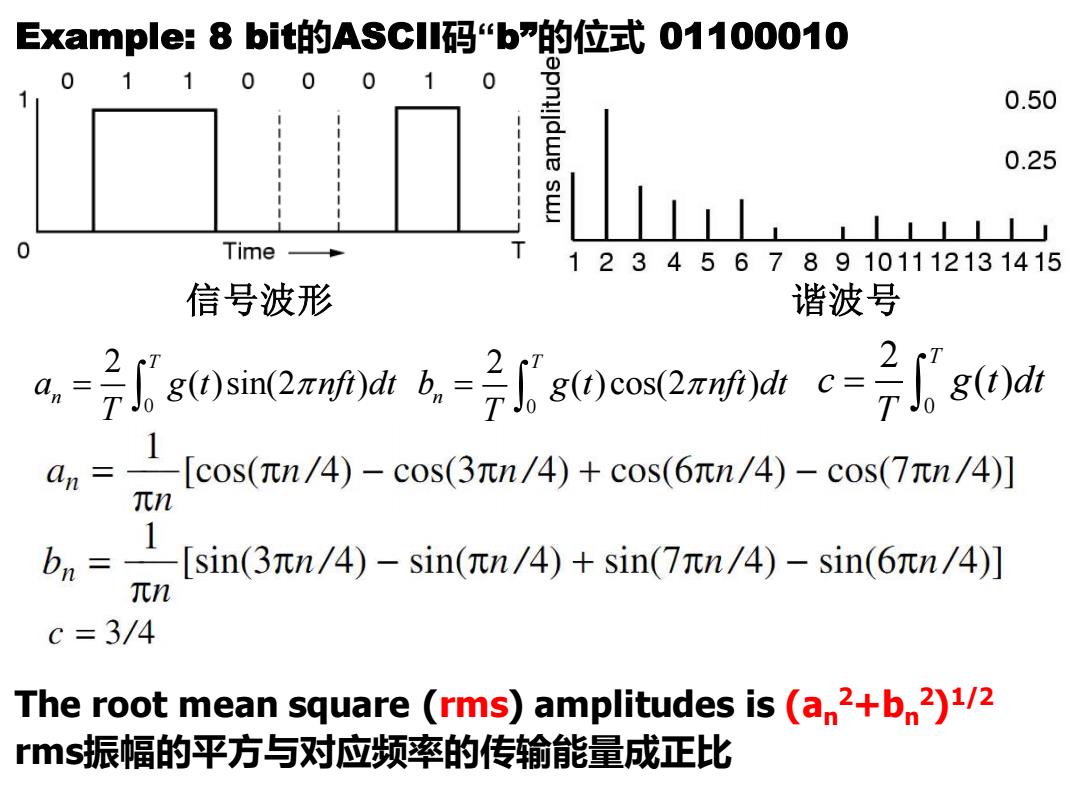
xample:8bit的ASC1l码“b的位式01100010 11000 1 0 0.50 0.25 0 Time 123456789101112131415 信号波形 谐波号 )sin(2ngdr)co2drd a,= an [cos(πn/4)-cos(3πn/4)+cos(6πn/4)-cos(7πn/4)] 元n 1 [sin(3元n/4)-sin(πn/4)+sin(7πn/4)-sin(6πn/4)] 元n c=3/4 The root mean square(rms)amplitudes is (an2+bn2)1/2 rms振幅的平方与对应频率的传输能量成正比
信号波形 谐波号 Example: 8 bit的ASCII码“b”的位式 01100010 The root mean square (rms) amplitudes is (an 2+bn 2) 1/2 rms振幅的平方与对应频率的传输能量成正比 0 2 ( )sin(2 ) T n a g t nft dt T = 0 2 ( )cos(2 ) T n b g t nft dt T = 0 2 ( ) T c g t dt T =
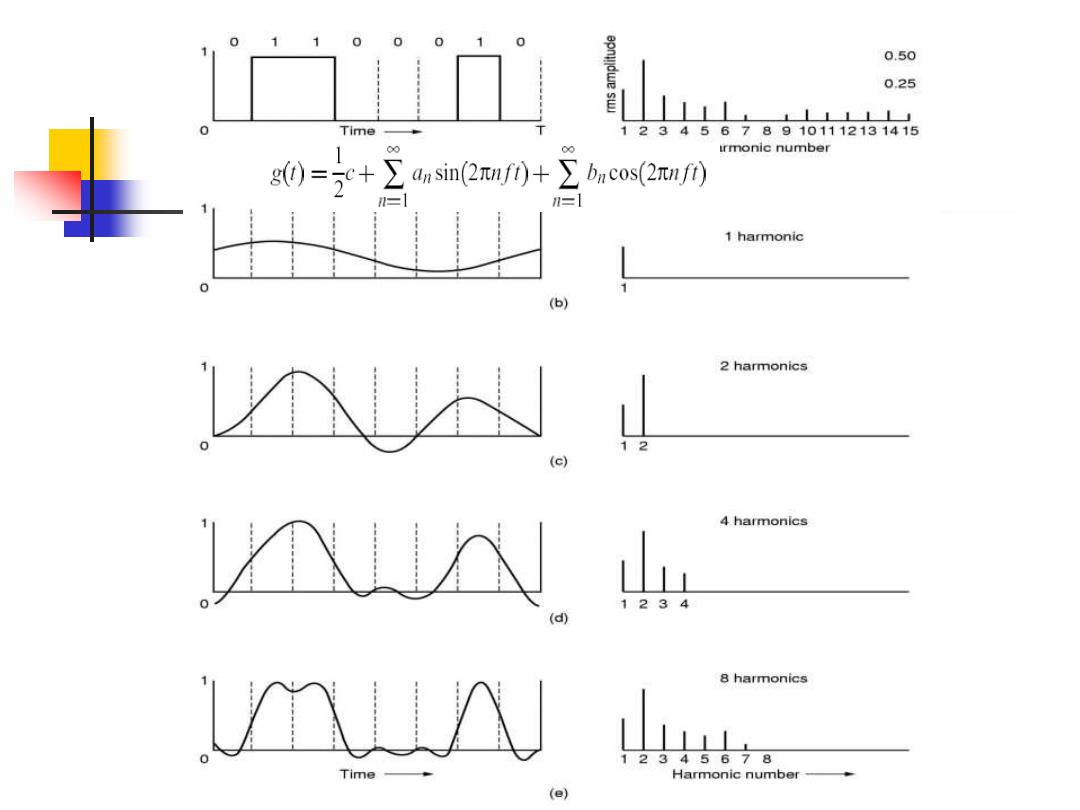
11000 1 0 0.50 0.25 Time 123456789101112131415 rmonic number g0=c+∑ansin(2uf0+∑bncos((2uf) 1 harmonic (b) 2 harmonics 12 (c) 4 harmonics 1234 d 8 harmonics Uiin 1234567 8 Time Harmonic number (e)

带宽 信号在物理介质中的传输总会有衰减, 从O到某一个频率fc,若对应Fourier分 量(谐波)振幅不会有明显减弱,这段 频率范围被称为带宽 ·fc:截止频率,通常为保留一半能量的频率 带宽由物理介质的材料构成、厚度和长 度等来决定
带宽 ◼ 信号在物理介质中的传输总会有衰减, 从0到某一个频率fc,若对应Fourier分 量(谐波)振幅不会有明显减弱,这段 频率范围被称为带宽 ◼ fc:截止频率,通常为保留一半能量的频率 ◼ 带宽由物理介质的材料构成、厚度和长 度等来决定
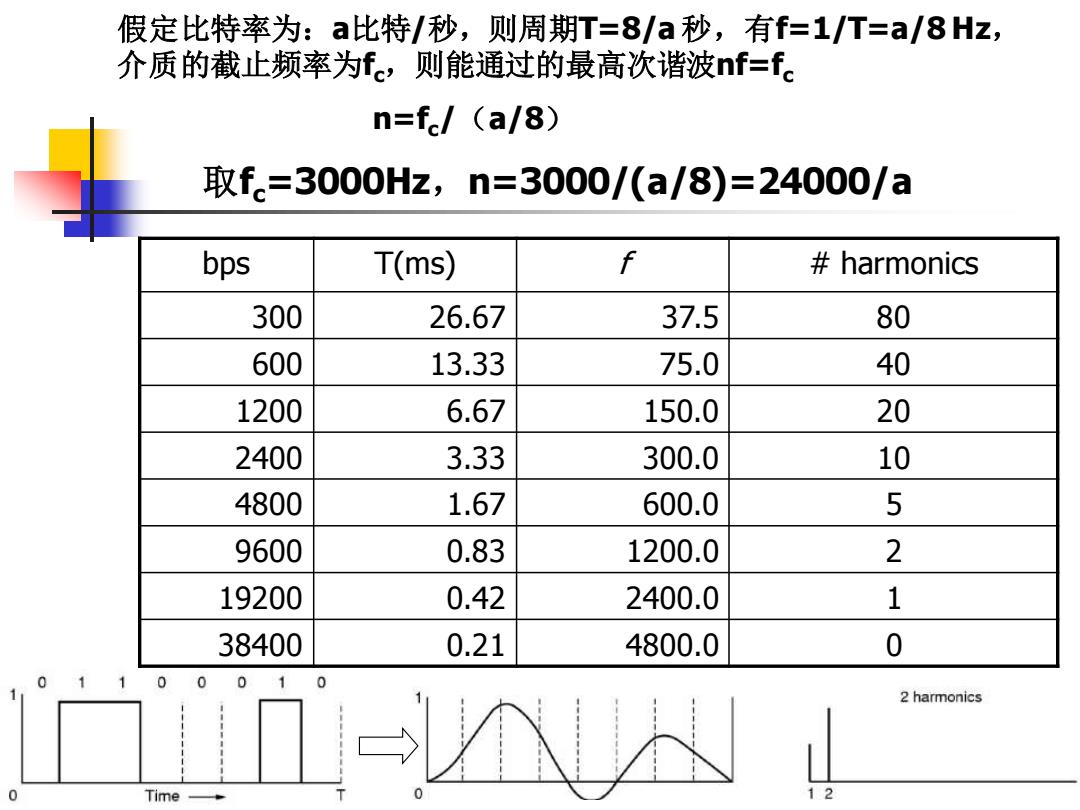
假定比特率为:a比特/秒,则周期T=8/a秒,有f=1/T=a/8Hz, 介质的截止频率为fc,则能通过的最高次谐波nf=fc n=fe/(a/8) 取f=3000Hz,n=3000/(a/8)=24000/a bps T(ms) f harmonics 300 26.67 37.5 80 600 13.33 75.0 40 1200 6.67 150.0 20 2400 3.33 300.0 10 4800 1.67 600.0 5 9600 0.83 1200.0 2 19200 0.42 2400.0 1 38400 0.21 4800.0 0 01100 0 1 0 2 harmonics 入 0 Time- 12
bps T(ms) f # harmonics 300 26.67 37.5 80 600 13.33 75.0 40 1200 6.67 150.0 20 2400 3.33 300.0 10 4800 1.67 600.0 5 9600 0.83 1200.0 2 19200 0.42 2400.0 1 38400 0.21 4800.0 0 取fc=3000Hz,n=3000/(a/8)=24000/a 假定比特率为:a比特/秒,则周期T=8/a 秒,有f=1/T=a/8 Hz, 介质的截止频率为fc,则能通过的最高次谐波nf=fc n=fc/(a/8)