非理想观察模型(信息传递系统的抽象) [X,P] [y.A] 信源 观察过程 P) 卫x一先验概率 P2x) P(x) 阝xr一后验概率 2 P) 转移概率 P(x) P(x) 传递的信息=先验不确定性一后验不确定性 第2章信息的度量 信息理论与编码 6
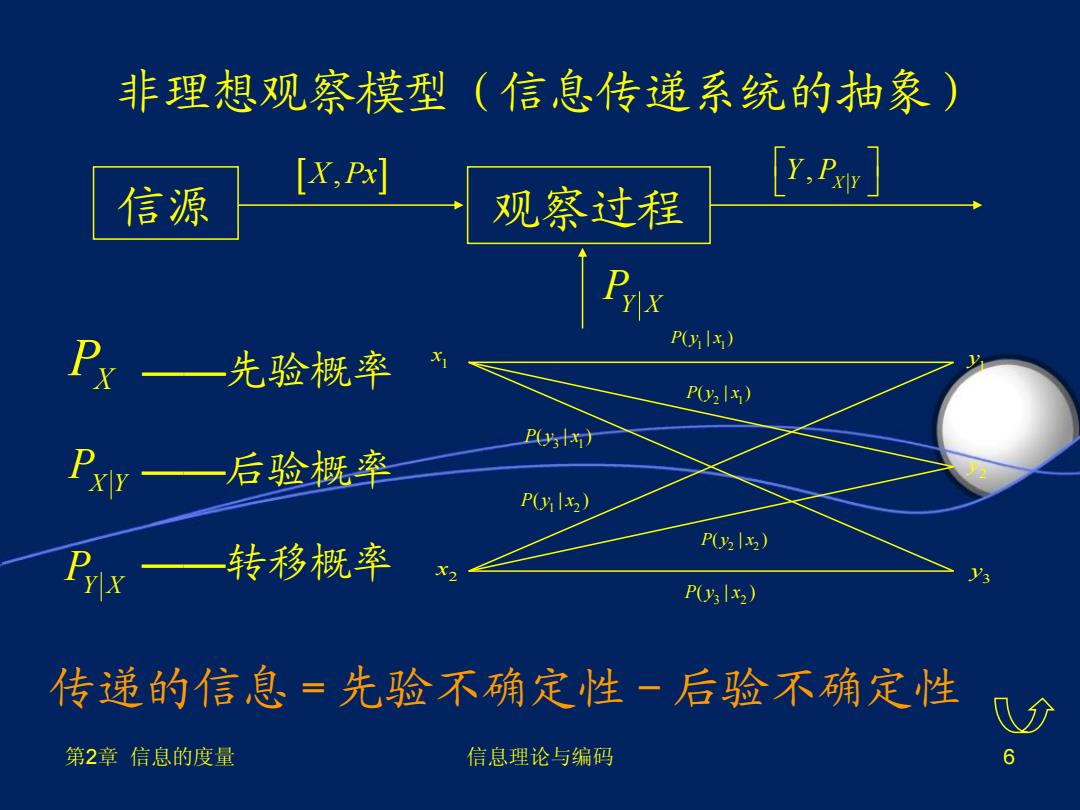
第2章 信息的度量 信息理论与编码 6 非理想观察模型(信息传递系统的抽象) ——先验概率 ——后验概率 ——转移概率 传递的信息=先验不确定性-后验不确定性 1 1 P y x ( | ) 1 x 2 x 3 y 2 y 1 y 2 2 P y x ( | ) 2 1 P y x ( | ) 1 2 P y x ( | ) 3 1 P y x ( | ) 3 2 P y x ( | ) PX PX Y PY X 信源 观察过程 X Px , , X Y Y P PY X

2、信息量及其性质 (1)自信息量及其性质 自信息量 1()=lo=-log()12 表示了信源符号的先验不确定性 单位:bit/符号 取2为对数底 联合自信息量I(xk,y,)=-logP(x,y) 表示二元符号的先验不确定性。 单位:bit/二元符号 第2章信息的度量 信息理论与编码 7
第2章 信息的度量 信息理论与编码 7 2、信息量及其性质 (1)自信息量及其性质 自信息量 表示了信源符号的先验不确定性 单位:bit/符号 取2为对数底 联合自信息量 表示二元符号的先验不确定性。 单位:bit/二元符号 1 ( ) log log ( ) ( ) k k k I x P x P x k K 1 , 2 , , ( , ) log ( , ) k j k j I x y P x y

条件自信息量 I(xy)=-log P(xy) 表示观察到y,符号的条件下x还剩下的 不确定性。 单位:bit/符号 I(y)=-log P(Y) 表示输入x且观察到y时干扰引入的不 确定性。 单位:bit/符号 第2章信息的度量 信息理论与编码 8
第2章 信息的度量 信息理论与编码 8 条件自信息量 表示观察到 符号的条件下 还剩下的 不确定性。 单位:bit/符号 表示输入 且观察到 时干扰引入的不 确定性。 单位:bit/符号 ( | ) log ( | ) k j k j I x y P x y ( | ) log ( | ) j k j k I y x P y x k x k x j y j y

例甲在一8×8的方格棋盘上随意放入一 个棋子,在乙看来棋子落入的位置是不确 定的。 (1)在乙看来,棋子落入某方格的不 确定性为多少? (2)若甲告知乙棋子落入方格的行号, 这时,在乙看来棋子落入某方格的 不确定性为多少? 第2章信息的度量 信息理论与编码 9
第2章 信息的度量 信息理论与编码 9 例 甲在一8×8的方格棋盘上随意放入一 个棋子,在乙看来棋子落入的位置是不确 定的。 (1)在乙看来,棋子落入某方格的不 确定性为多少? (2)若甲告知乙棋子落入方格的行号, 这时,在乙看来棋子落入某方格的 不确定性为多少?

解将棋子方格从第一行开始按顺序编号 得到一个序号集合{z,|1=1,2,…,64),棋子 落入的方格位置可以用取值于序号集合的随 机变量Z来描述,即乙={z,|1=1,2,…,64} (1)由于棋子落入任一方格都是等可能 的,则 P(z,) =1.2 ··,64 棋子落入某方格的不确定性就是自信息量 E)-1gre)=-le4 6 bit/符号 第2章信息的度量 信息理论与编码 10
第2章 信息的度量 信息理论与编码 10 解 将棋子方格从第一行开始按顺序编号, 得到一个序号集合 ,棋子 落入的方格位置可以用取值于序号集合的随 机变量 来描述,即 (1)由于棋子落入任一方格都是等可能 的,则 棋子落入某方格的不确定性就是自信息量 bit/符号 { | 1, 2, ,64} l z l Z Z z l { | 1, 2, ,64} l 1 ( ) 1,2, ,64 64 P z l l 1 ( ) log ( ) log 6 64 l l I z P z