响应曲线有四种: h(t) θt) h(0 00) (a) (b) 有自衡的非振荡过程 h(t) c(0) (a) (b) 无自衡的非振荡过程
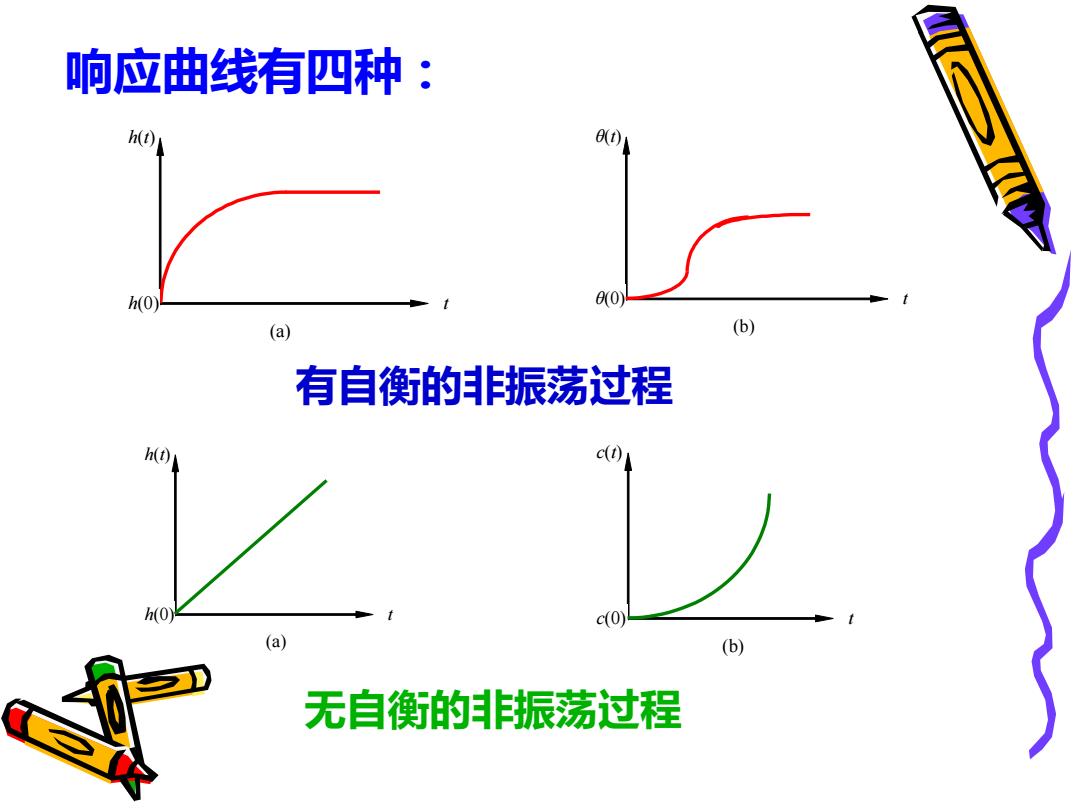
响应曲线有四种: h(t) h(0) t (a) θ(t) θ(0) t (b) 有自衡的非振荡过程 h(t) h(0) t (a) c(t) c(0) t (b) 无自衡的非振荡过程

c(1) c() c(0 c(0) 有自衡的振荡过程 具有反向特性的过程
c(t) c(0) t c(t) c(0) t 有自衡的振荡过程 具有反向特性的过程
有自衡的非振荡过程如下图中的液位过程 F h(t) h h0) (a) F2
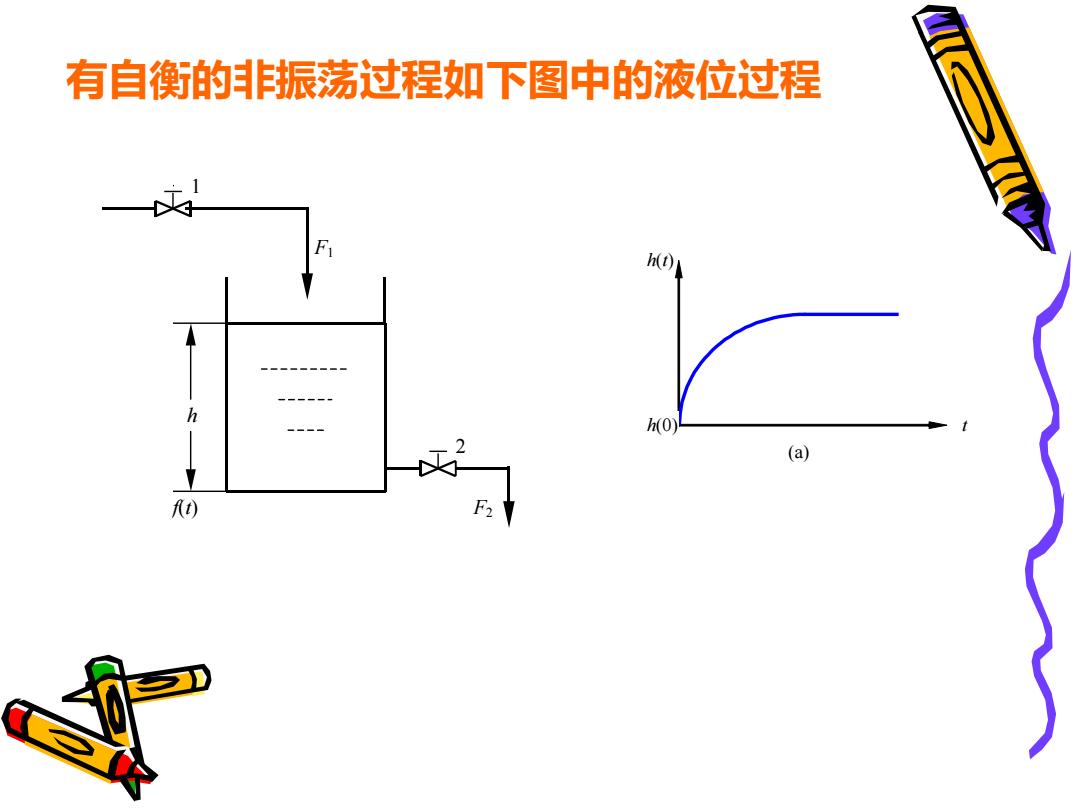
f(t) 1 F1 F2 2 h 有自衡的非振荡过程如下图中的液位过程 h(t) h(0) t (a)
无自衡的非振荡过程如下图中的液位过程 h(t) h(0 (a) F2 同
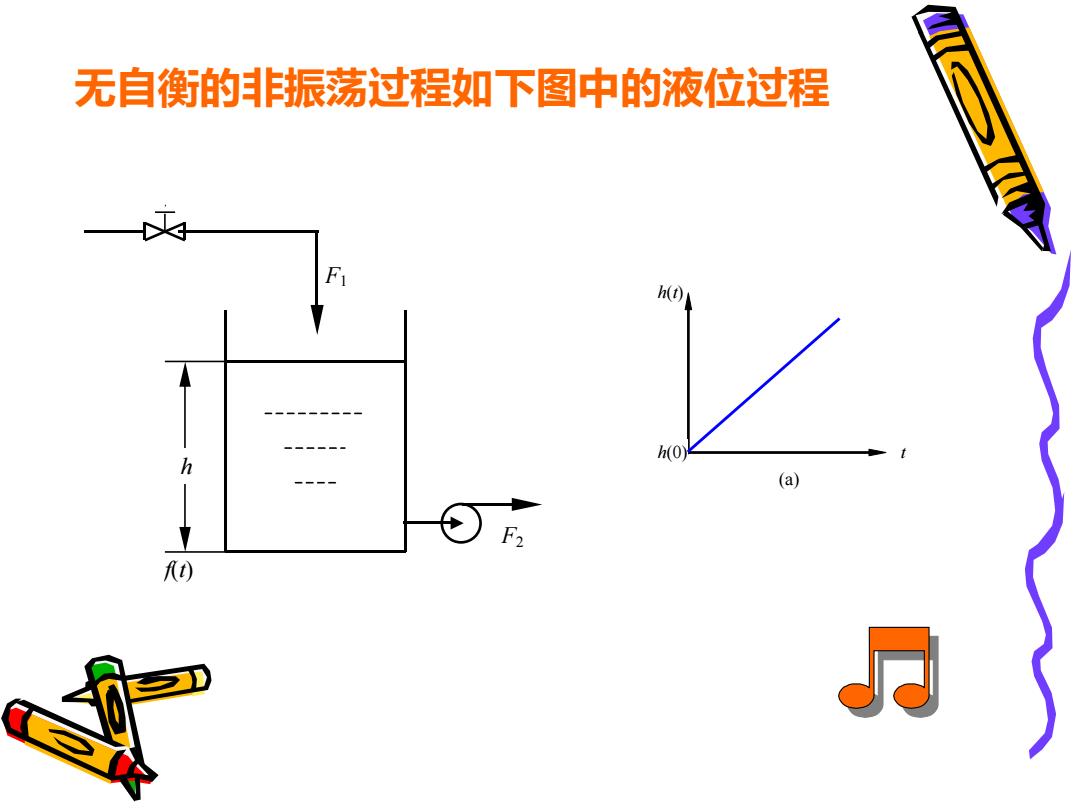
f(t) F1 F2 h 无自衡的非振荡过程如下图中的液位过程 h(t) h(0) t (a)

2.2过程的数学描述 要研究被控过程的特性,就必须知道被控过程的 数学模型(参量模型),也就是对过程的数学描述。 数学模型:表示具体过程的输入、输出关系的数学方 程式。 其形式有:微分方程式、偏微分方程式、状态方程 热物料 蒸汽加 蒸汽 热器 冷物料
2.2 过程的数学描述 要研究被控过程的特性,就必须知道被控过程的 数学模型(参量模型),也就是对过程的数学描述。 数学模型:表示具体过程的输入、输出关系的数学方 程式。 其形式有:微分方程式、偏微分方程式、状态方程 热物料 冷物料 蒸汽 蒸汽加 热器