
贝叶斯估计一最小风险 第三章 口损失函数:把日估计为所造成的损失,记为 2(8,0) 概率密度函数的估计 口期望风险: R-SSi0.0)p(x.0x0ds 2009-10-20 p)p(xdods =jep。(0,p01xded R(x)p(x)ds: 口条件风险: R(x)=2(00)p(0lxyio. 贝叶斯估计一最小风险 贝叶斯估计一最小风险 口最小化期望风险)最小化条件风险。 口把损失函数定义为平方误差:2(0,0)=(0-0)2 口在有限样本集下,最小化经验风险 R(lx)=[1(0,0)p(olx)do R(1K)=[1(0.0)p(olke. =J。B-E(e1x)p(e1x)d0+∫.[E(a1x)-p01x)de, 口贝叶斯估计量:(在样本集K下)是条件风险 口定理:如果采用平方损失函数,则有 (经验风险)最小的估计量睡,即 iaE=E[01x]=∫。0p(01x)d0; O=arg min R(K). 口同理,在给定样本集K下,日的贝叶斯估计是 6aE=E01K]=J。0p(01K)d0; 贝叶斯估计一最小风险 一元正态分布的贝叶斯估计 口平方误差损失下,求解贝叶斯估计的步骤: 口总体分布密度为: ■确定日的先验分布p()方 p(x|4)~N(4,o2)5 ■由样本集K=x,2,xw}求出样本集的联合分 布: pKIo)=立pIo: 口均值μ未知,μ的先验分布为: p(4)~N(4o,o); ■计算日的后验分布 n01K)0poao p(K)p(0) 口样本集:K={x,x2,,w} ■计算贝叶斯估计 =fop(o1K)do. 口用贝叶斯估计方法求μ的估计量
第三章 概率密度函数的估计 2009-10-20 2 贝叶斯估计 — 最小风险 损失函数:把θ估计为 所造成的损失,记为 期望风险: 条件风险: ˆ ( ˆ, )。 ˆ (, ) (, ) ˆ (, ) ( | )() ˆ () (, ) ( | ) ˆ ( | ) () ; d d d d E E E E R p dd p p dd p p dd R pd x x xx x x xx x xx ˆ ˆ R pd ( | ) (,)( | ) . x x 3 贝叶斯估计 — 最小风险 最小化期望风险 最小化条件风险。 在有限样本集下,最小化经验风险 贝叶斯估计量:(在样本集 K 下)是条件风险 (经验风险)最小的估计量 ,即 ˆ ˆ R pd ( | ) (,)( | ) . K K BE ˆ BE ˆ ˆ ˆ arg min ( | ). R K 4 贝叶斯估计 — 最小风险 把损失函数定义为平方误差: 定理:如果采用平方损失函数,则有 同理,在给定样本集K 下,θ的贝叶斯估计是 2 2 ˆ ˆ ( | ) (,)( | ) ˆ [ ( | )] ( | ) [( | ) ]( | ) ; R pd E pd E pd x x xx x x 2 ˆ ˆ ( , ) ( ). B E ˆ E [|] (|) ; p d x x B E ˆ E [| ] (| ) ; p d K K 5 贝叶斯估计 — 最小风险 平方误差损失下,求解贝叶斯估计的步骤: 确定θ的先验分布 p(θ); 由样本集 K={x1, x2 ,…, xN} 求出样本集的联合分 布: 计算θ的后验分布 计算贝叶斯估计 1 ( | ) ( | ); N k k p p K x ( | )() (| ) ; ( | )() p p p p p d K K K B E ˆ p ( | ) . d K 6 一元正态分布的贝叶斯估计 总体分布密度为: 均值μ未知,μ的先验分布为: 样本集: K={x1, x2 ,…, xN} 用贝叶斯估计方法求μ的估计量 2 px N ( | ) ~ ( , ); 2 0 0 p N ( ) ~ ( , );

一元正态分布的贝叶斯估计 一元正态分布的贝叶斯估计 口计算u的后验分布 口计算μ的贝叶斯估计 p(K)=P(KI)p() i=∫4p(μ|K)du=4w; p(K) ■是样本信息和先验知识的线性组合。 -a p(sp()-Nx) 口当N=0时,户E=o k1 口当N→∞时,户E→mv 4w= Nog 02 Cug? Naia mNNa ■特例: 口如三0,则应E=4:即先验知识可靠,样本 其中m,=之为样本均值 不起作用。 N台 口如0n>G,则户E=mv;即先验知识十分不确 定,完全依靠样本信息。 贝叶斯学习 贝叶斯学习 口由局部推导总体:利用日的先验分布p(日)及训 口考虑学习样本个数N,记样本集N={x,,xw}; 练样本提供的信息(似然函数)p日),求出 日的后验分布p(),然后直接求总体分布。 口当N>1时, p(xIK)=p(x,01k)de p(KN10)=p(xx10)p(K10) =[p(x10,K)p(0K)de =「p(x|0)p(01K)d0; 口因此,有递推后验概率公式: ■把类条件概率密度(总体分布)p)和未知参 p(xx 10)p(01Kx-) 数的后验概率密度p()联系起来。 p(01K*)=- p(xx 10)p(01K-)do ■贝叶斯解的结果与最大似然估计的结果近似相等 p|K)≈p(x|dm). 11 贝叶斯学习 一元正态分布的贝叶斯学习 口参数估计的递推贝叶斯方法(Recursive Bayes 口计算μ的后验分布 Incremental Learning) P(K)=P(K I)p() ■设p(0|K)=p(0),当样本数目增多,可得到后 p(K) 验概率密度函数序列:p(),p(0川x),p(01x,2,… -a p(s.)p()-N(x) ■贝叶斯学习(Bayesian Learning)性质:如果此 序列收敛予以真实数值为中心的δ函数,即 Nag 2 MN= p(01KN→)=6(0-0)5 Na+ay+ ag+o?lo,ai= dig Nap+ai x为样本均值 p(x|KN→)=p(x|6=0。)=p(x) 其中m=N 当N→时,→0,p叫)→函数
7 一元正态分布的贝叶斯估计 计算μ的后验分布 2 1 ( | )() (| ) ( ) ( | ) ( )~ ( , ) N k NN k p p p p px p N K K K 2 22 2 0 0 2 22 22 22 0 00 0 1 , 1 ; NN N N N k k N m NN N m N x ; 其中 为样本均值 8 一元正态分布的贝叶斯估计 计算μ的贝叶斯估计 是样本信息和先验知识的线性组合。 当 N=0 时, 当N→∞时, 特例: 如 ,则 即先验知识可靠,样本 不起作用。 如 ,则 即先验知识十分不确 定,完全依靠样本信息。 ˆ (| ) ; N p d K ˆ ; BE 0 ˆ ; BE N m 0 2 0 0 ˆ ; BE n ˆ ; BE N m 9 贝叶斯学习 由局部推导总体:利用θ的先验分布 p(θ)及训 练样本提供的信息(似然函数)p(K|θ),求出 θ的后验分布p(θ|K) ,然后直接求总体分布。 把类条件概率密度(总体分布)p(x|K) 和未知参 数的后验概率密度 p(θ|K) 联系起来。 贝叶斯解的结果与最大似然估计的结果近似相等 ( | ) (, | ) (|, )(| ) (|)(| ) ; p pd p p d pp d x x x x K K K K K ML ˆ p p (x x | K) ( | ). 10 贝叶斯学习 考虑学习样本个数N,记样本集 KN={x1,…, xN} ; 当 N>1时, 因此,有递推后验概率公式: 1 ( | ) ( | ) ( | ); N N N p pp K K x 1 1 ( | ) ( | ) ( | ) ; ( |)(| ) N N N N N p p p p p d x x K K K 11 贝叶斯学习 参数估计的递推贝叶斯方法(Recursive Bayes Incremental Learning) 设 ,当样本数目增多,可得到后 验概率密度函数序列: 贝叶斯学习(Bayesian Learning)性质:如果此 序列收敛予以真实数值为中心的δ函数,即 ( | ) ( ) 0 p K p 1 12 pp p ( ), ( | x xx ), ( | , ), 0 ( | ) ( ); N p K 0 ˆ ( | ) ( | ) ( ). N ppp xxx K 12 一元正态分布的贝叶斯学习 2 1 ( | )() (| ) ( ) ( | ) ( ) ~ ( , ); N k NN k p p p p px p N K K K 2 22 2 0 0 2 22 22 22 0 00 0 1 , 1 ; NN N N N k k N m NN N m N x ; 其中 为样本均值 计算μ的后验分布 2 N 0 N 当 时, , ( | ) 函数。 p K

一元正态分布的贝叶斯学习 一元正态分布的贝叶斯学习 口直接计算总体密度: PNur,3,x. p(xK)=[p(xlu)p(ulK)du 2石+op} ~N(4,o2+o). 均值4x 方差由σ增为σ+σ:由于用了以的估计值而不确定性增加 非监督参数估计(简介) 非监督参数估计(简介) 口样本类别未知,但各类条件概率密度函数的形式 口非监督最大似然估计的思路: 已知,根据所有样本估计各类密度函数中的参数。 ■最大似然估计 口非监督最大似然估计的思路: ■混合密度:分量密度的线性组合 i=Ems·pto)=gmg立npIo: le,P) ■可识别性问题:未知参数的个数小于等于独立方 程的个数。 ■似然函数和对数似然函数 ■计算问题:微分方程组 0=pK0=·px,0 V.H©=0,i=12.,c H(0)=In0)=In p(x,10) 口常采用选代法进行参数估计, 总结:参数估计 讨论:参数估计中的模型选择 口最大似然估计 口实际工作中处理的大都是高维数据:d>10。 On =arg max p(K10)=arg max p(x10) 口统计学中经典的多元(高维)分布很少,研究的 口最大后验概率估计 最详尽的是多元正态分布。 =arg max p(K1)p(0)=arg maxI p(x+p(). 口近几十年的研究发现,实际所处理的高维数据几 口贝叶斯估计 乎都不服从正态分布。 P(01K)=P)E(01K)-J0p(01Kd0. 口通过增加模型的复杂程度(参数的个数),如正 p(K10)p(0)de 态模型的线性组合一高斯混合模型,试图“逼近” 口贝叶斯学习 真实的分布,出现了过拟合问题。 p(xK)=[p(x10)p(1K)de
13 一元正态分布的贝叶斯学习 14 一元正态分布的贝叶斯学习 直接计算总体密度: 2 22 22 2 2 (| ) (| )( | ) 1 1 exp 2 2 ~ ( , ). N N N N N px px p d x N K K 15 非监督参数估计(简介) 样本类别未知,但各类条件概率密度函数的形式 已知,根据所有样本估计各类密度函数中的参数。 非监督最大似然估计的思路: 混合密度:分量密度的线性组合 似然函数和对数似然函数 16 非监督参数估计(简介) 非监督最大似然估计的思路: 最大似然估计 可识别性问题:未知参数的个数小于等于独立方 程的个数。 计算问题:微分方程组 常采用迭代法进行参数估计。 1 1 ˆ arg max ( | ) arg max ln ( | ); N N k k k k px px 17 总结:参数估计 最大似然估计 最大后验概率估计 贝叶斯估计 贝叶斯学习 ML 1 ˆ arg max ( | ) arg max ( | ); N k k p p K x MAP 1 ˆ arg max ( | ) ( ) arg max ln ( | ) ln ( ); N k k pp p p K x BE ( | )() ˆ (| ) , (| ) (| ) ; ( | )() p p p E pd p pd K K KK K p pp d (| ) (|)(| ) . x x K K 18 讨论:参数估计中的模型选择 实际工作中处理的大都是高维数据:d≥10。 统计学中经典的多元(高维)分布很少,研究的 最详尽的是多元正态分布。 近几十年的研究发现,实际所处理的高维数据几 乎都不服从正态分布。 通过增加模型的复杂程度(参数的个数),如正 态模型的线性组合—高斯混合模型,试图“逼近” 真实的分布,出现了过拟合问题

非参数估计 概率密度函数的估计方法分类 口非参数估计:密度函数的形式未知,也不作假 设,利用训练数据直接对概率密度进行估计。又 Density Estimation 称作模型无关方法。 ■参数估计需要事先假定一种分布函数,利用样本 metric 数据估计其参数。又称作基于模型的方法。 Semi-parametric ■任何非参数估计方法都需要选择平滑参数。 口主要方法: ■直方图法 ■核函数方法(Parzen窗法) ■K。~近邻法 21 直方图法 直方图法 口最简单的非参数概率密度估计方法。 口平滑参数:小窗个数/尺寸(bin size) 口基本思路:P(x)是p()的一个离散近似。 M=3 P(x) M=20 p(x) p(x). ·把观测向量x的每个分量分成k个等间隔小窗 (bin):xEE,则形成个小舱; ■统计落入各个小舱内的样本数 Oversmoothing H0=1xeB).i=1.2.….m M=10 =50 p(x) ■正规化 D H(i) P()-HU) “Overfitting 2 直方图法 非参数估计的基本方法 口优点 口问题:已知样本集K={x,x2,xn},其中的样 ■计算快速、直观易理解; 本均从服从(x)的总体中独立抽取,估计样本 ■直方图一旦建好,即不再需要训练数据: 空间中任何一点的概率密度Px),以近似)。 ■只保留与直方图小舱的位置和大小相关的信息: ■可顺序建立直方图,即每次考虑一个数据后丢弃。 口基本思路:用某种核函数表示某一样本对待估计 口缺点 的密度函数的贡献,所有样本所作贡献的线性组 ■估计的概率密度不平滑,在小舱边界不连续; 合(函数之和)视作对某点概率密度(x)的估计 ■对小窗个数/尺寸非常敏感; ■在高维空间的推广性不好(数据稀疏)。 )=p(x- o改进:Data-adaptive histogram,naive Bayes,Dependence trees
19 非参数估计 非参数估计:密度函数的形式未知,也不作假 设,利用训练数据直接对概率密度进行估计。又 称作模型无关方法。 参数估计需要事先假定一种分布函数,利用样本 数据估计其参数。又称作基于模型的方法。 任何非参数估计方法都需要选择平滑参数。 主要方法: 直方图法 核函数方法(Parzen窗法) kn-近邻法 20 概率密度函数的估计方法分类 21 直方图法 最简单的非参数概率密度估计方法。 基本思路: 是 的一个离散近似。 把观测向量 x 的每个分量分成 k 个等间隔小窗 (bin);x∈Ed,则形成 kd 个小舱; 统计落入各个小舱内的样本数 正规化 ( ) ˆ P x p( ) x 22 直方图法 平滑参数:小窗个数/尺寸(bin size) 23 直方图法 优点 计算快速、直观易理解; 直方图一旦建好,即不再需要训练数据; 只保留与直方图小舱的位置和大小相关的信息; 可顺序建立直方图,即每次考虑一个数据后丢弃。 缺点 估计的概率密度不平滑,在小舱边界不连续; 对小窗个数/尺寸非常敏感; 在高维空间的推广性不好(数据稀疏)。 改进:Data-adaptive histogram,naive Bayes,Dependence trees… 24 非参数估计的基本方法 问题:已知样本集 K= {x1, x2,…, xn},其中的样 本均从服从 的总体中独立抽取,估计样本 空间中任何一点的概率密度 ,以近似 。 基本思路:用某种核函数表示某一样本对待估计 的密度函数的贡献,所有样本所作贡献的线性组 合(函数之和)视作对某点概率密度p(x)的估计。 ( ) ˆ P x p( ) x p( ) x 1 ˆ ( ) ( ). n N i i p x xx
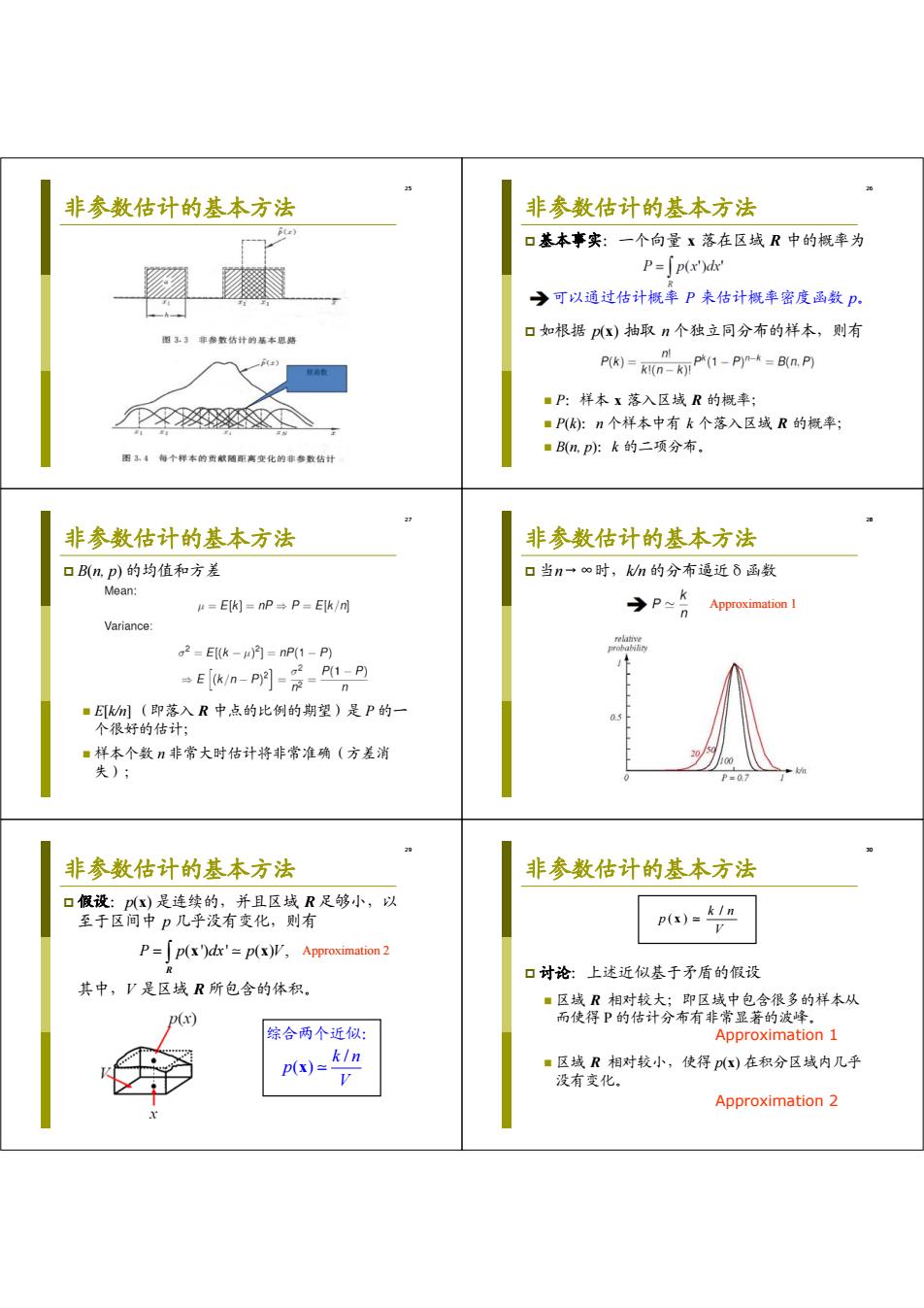
非参数估计的基本方法 非参数估计的基本方法 B) 口基本事实:一个向量x落在区域R中的概率为 P=「p(x')d →可以通过估计概率P来估计概率密度函数P。 图3.3非参数结计的基本思贴 口如根据p(x)抽取n个独立同分布的样本,则有 nl P(k)KI()(1-P)--B(n.P) ■P:样本x落入区域R的概率; ■P:n个样本中有k个落入区域R的概率: ■B(np吵:k的二项分布。 图34每个样本的货献随距离变化的非参数估计 非参数估计的基本方法 非参数估计的基本方法 口B(n,p)的均值和方差 口当n一∞时,n的分布逼近δ函数 Mean: r=Ek)=nP→P=Ek/m →P 2 Approximation I Variance: relative a2=E(k-)月=nP(1-P) En-明-爱A,A ■E例(即落入R中点的比例的期望)是P的一 个很好的估计; ■样本个数n非常大时估计将非常准确(方差消 失); P=0.7 非参数估计的基本方法 非参数估计的基本方法 口假设:p(x)是连续的,并且区域R足够小,以 至于区间中p几乎没有变化,则有 P()=1n P=p(x)dx'=p(x)V,Approximation2 口讨论:上述近似基于矛盾的假设 其中,V是区域R所包含的体积。 ■区域R相对较大;即区域中包含很多的样本从 D(x) 而使得P的估计分布有非常显著的波峰。 综合两个近似: Approximation 1 p(x)=kin ■区域R相对较小,使得x)在积分区域内几乎 没有变化。 Approximation 2
25 非参数估计的基本方法 26 非参数估计的基本方法 基本事实:一个向量 x 落在区域 R 中的概率为 可以通过估计概率 P 来估计概率密度函数 p。 如根据 p(x) 抽取 n 个独立同分布的样本,则有 P:样本 x 落入区域 R 的概率; P(k):n 个样本中有 k 个落入区域 R 的概率; B(n, p):k 的二项分布。 27 非参数估计的基本方法 B(n, p) 的均值和方差 E[k/n] (即落入 R 中点的比例的期望)是 P 的一 个很好的估计; 样本个数 n 非常大时估计将非常准确(方差消 失); 28 非参数估计的基本方法 当n→∞时,k/n 的分布逼近δ函数 Approximation 1 29 非参数估计的基本方法 假设:p(x) 是连续的,并且区域 R 足够小,以 至于区间中 p 几乎没有变化,则有 其中,V 是区域 R 所包含的体积。 P p dx p V ( ') ' ( ) , x x R Approximation 2 / ( ) k n p V x 综合两个近似: 30 非参数估计的基本方法 讨论:上述近似基于矛盾的假设 区域 R 相对较大;即区域中包含很多的样本从 而使得 P 的估计分布有非常显著的波峰。 Approximation 1 区域 R 相对较小,使得 p(x) 在积分区域内几乎 没有变化。 Approximation 2 / ( ) k n p V x