北京大学：《模式识别》课程教学资源（课件讲稿）特征的选择和提取（第二部分）

7.4基于概率分布的可分性判据 第七章 口考查两类分布密度之间的交叠程度 特征的选择与提取 p(da) 完全可分 2009-12-1 P)=P) p(x@)=p(x@2) 完全不可分 P()=P() 7.4基于概率分布的可分性判据 7.4.1常用的概率距离度量 口定义：两个密度函数之间的距离 Bhattacharyya距离 J=∫g[p(xl0).p(x|a),,h J。=--InSIp(xI0)pxa,2dk ■须满足如下条件： 1.J,是非负，即J。≥0 1)两类完全重合时，JB=0: 2)两类完全不交叠时，JB=∞ 2当两类完全不交叠时，J。达到其最大值，即 3)与错误概率的上界有直接关系： if p(xl)p(xl)=0,Vx,thenJ=J 3.当两类分布密度相同时，J。=0: P≤[P(@)P(@,exp-Ja】 if p(xla)=p(x2),Vx,then J=0. 7.4.1常用的概率距离度量 7.4.1常用的概率距离度量 口Chernoff.界 口散度(Divergence)) Jc=-InSp"(xl@)p(xI@x,se[0.I] ■利用对数似然比（或似然比），对于某特征值x )3=0.5,Jc=Ja (x)=In p(xl@) p(x @, 2)fors∈0，l]Je20; 3)fors∈0，】Je=0台pxla)=p(xo,x 口px|a)=p|o)→1，(x)=0 4)当x的各分量彼此独立时， 口p(xo)和p(xo)差异越大，，（越大： Je()(t ■考虑整个特征空间概率分布的差异，分别定义对 0,类及对四，类的平均可分性信息 5)当x的各分量彼此独立时 ,==j1eh2e,,=印，x Jc(,x,x2,…X)≤Jc(Sx,x2,…x,x) p(xlo,)

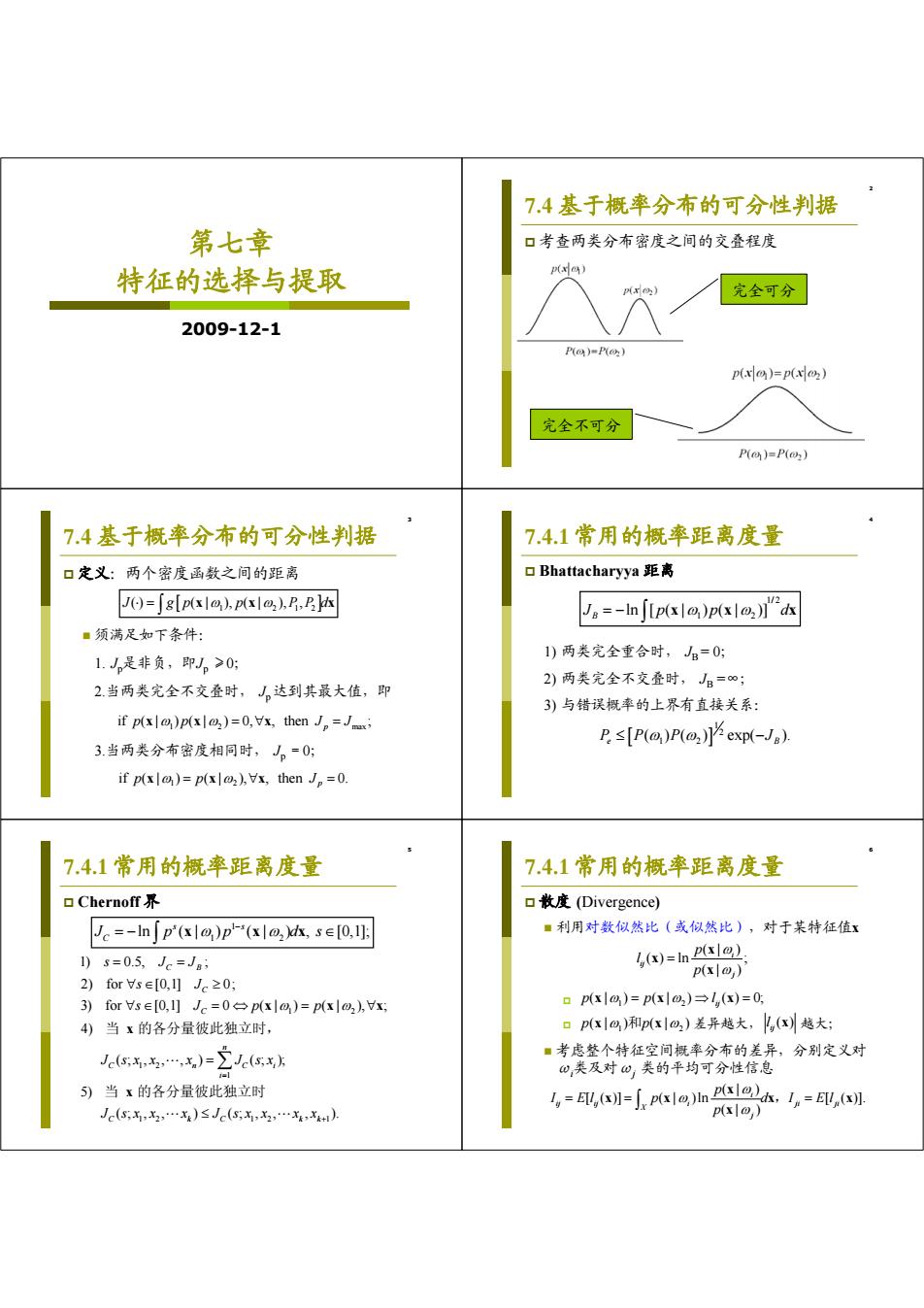
第七章 特征的选择与提取 2009-12-1 2 7.4 基于概率分布的可分性判据  考查两类分布密度之间的交叠程度 完全可分 完全不可分 3 7.4 基于概率分布的可分性判据  定义：两个密度函数之间的距离  须满足如下条件： 1. Jp是非负，即Jp ≥0； 2.当两类完全不交叠时， Jp 达到其最大值，即 3.当两类分布密度相同时， Jp ＝0；   1 2 12 J ( ) ( | ), ( | ), ,   g p p PPd    xx x 1 2 max if ( | ) ( | ) 0, , then ; p p p JJ xx x     1 2 if ( | ) ( | ), , then 0. p pp J x xx     4 7.4.1 常用的概率距离度量  Bhattacharyya 距离 1) 两类完全重合时， JB = 0； 2) 两类完全不交叠时， JB =∞； 3) 与错误概率的上界有直接关系： 1/2 1 2 ln [ ( | ) ( | )] B J   pp d    xx x  1 2 1 2 ( ) ( ) exp( ). PP P J e B     5 7.4.1 常用的概率距离度量  Chernoff 界 1 1 2 ln ( | ) ( | ) , [0,1]; s s C J p p ds       x xx 1 2 1 2 1 12 12 1 1) 0.5, ; 2) for [0,1] 0; 3) for [0,1] 0 ( | ) ( | ), ; 4) ( ; , , , ) ( ; ); 5) ( ; , , ) ( ; , , , ). C B C C n C n Ci i C k C kk s JJ s J sJp p J sx x x J sx J sx x x J sx x x x                 x xx x x    当 的各分量彼此独立时， 当 的各分量彼此独立时 6 7.4.1 常用的概率距离度量  散度 (Divergence)  利用对数似然比（或似然比），对于某特征值x   差异越大， 越大；  考虑整个特征空间概率分布的差异，分别定义对 ωi 类及对ωj 类的平均可分性信息 ( | ) ( ) ln ; ( | ) i ij j p l p    x x x 1 2 ( | ) ( | ) ( ) 0; ij pp l xx x     1 2 p p (x x | ) ( 和 | ) ( ) ij l x (| ) [ ( )] ( | )ln [ ( )]. (| ) i ij ij i ji ji X j p I El p d I El p       x xx x x x

7.4.1常用的概率距离度量 7.4.1常用的概率距离度量 口散度(Divergence) 口正态分布下的散度 ■定义区分®，类和⊙，类的总的平均信息（散度）： ■设两类别都是d维正态分布，分别表示为 o1,+!=f[p(x)-pI 0(μ2)，0（μj”2,则 p(xlo,) 1 p(x|o,)= 1)Jn≥0 2P1四cp-具，yx-4,月 2)Jn=0台pa)=pm,x 3)当x的各分量彼此独立时，J。:,,,x)-之JG o)2r2rp-j5x-4 4)当x的各分量彼此独立时， →对数似然比 J(2,)≤J(,2…X 6-3--3--安-r5- 5)Jn(4,2)=Jn(az,4) 7.4.1常用的概率距离度量 7.4.1常用的概率距离度量 口正态分布下的散度 口正态分布下的散度 ■利用矩阵迹的性质tr(BA=t(AB)(=AB,如 A,B是向量)，似然比可改写成 nnig,+-训 6--nga-X-7 +=,+a- 2 Mahalanobis +-- ■如果两类协方差矩阵相等，则 距离的平方 → J。=(-)》Eμ，-)=J 42到+-g】 在协方差矩阵相等条件下散度与很相 +(-P/XP-PYb 似，都是对样本在特征空间分散程度的描述。 11 7.4.1常用的概率距离度量 7.4.2概率距离判据下的特征提取 口正态分布下的Bhattacharyya距离 口基本方法：类似于距离度量下的特征提取 -到 ■设 (，-μ，） y=A'x, 侣 [巴巴， 求映射后的判据表达式（JJ。JD)对A的各分 量的偏导数并令其为零，得到所需的方程式组， ■如果两类协方差矩阵相等，则 然后用相应方法求解。 ■注意：原空间中一个矩阵W经映射后变为 8Ja=(μ，-μ，Σ-（μ，-μ）=JD=JM W'=A'WA

7 7.4.1 常用的概率距离度量  散度 (Divergence)  定义区分ωi 类和ωj 类的总的平均信息（散度）： ( | ) [ ( | ) ( | )]ln ; ( | ) i D ij ji i j X j p J II p p d p         x xx x x    1 2 1 2 1 12 12 1 12 21 1 0; 2 0 ( | ) ( | ), ; 3 ( , , , ) ( ); 4 ( , , ) ( , , , ); 5 , ,. D D n D n Di i D k D kk D D J Jpp J xx x J x J xx x J xx xx J J               x xx x x    ） ） ）当 的各分量彼此独立时， ）当 的各分量彼此独立时， ） 8 7.4.1 常用的概率距离度量  正态分布下的散度  设两类别都是 d 维正态分布，分别表示为 ωi ~N(μi ，∑i ) ，ωj ~N(μj ，∑j )，则 1 /2 1/2 1 /2 1/2 1 1 ( | ) exp[ ( ) ( )], (2 ) | | 2 1 1 ( | ) exp[ ( ) ( )]; (2 ) | | 2 T i ii i d i T j jj j d j p p             x x μ Σ x μ Σ x x μ Σ x μ Σ 11 1 1 1 ln | | ( ) ( ) ( ) ( ); 22 2 j T T ij i i i j j j i l          Σ x μ Σ x μ x μ Σ x μ Σ 对数似然比 9 7.4.1 常用的概率距离度量  正态分布下的散度  利用矩阵迹的性质 tr(BAT)=tr(ATB ) (=ATB ，如 A，B是向量) ，似然比可改写成 1 1 1 1 ln | | [ ( )( ) ] 2 2 1 [ ( )( ) ]; 2 j T ij i i i i T jjj l tr tr        Σ Σ x μ x μ Σ Σ x μ x μ 1 1 1 1 1 ln | | [ ( )] 2 2 1 [ ( )( ) ]; 2 j ij i j i i T ji ji j I tr tr         Σ ΣΣ Σ Σ Σμ μμ μ 10 7.4.1 常用的概率距离度量  正态分布下的散度  如果两类协方差矩阵相等，则 1 1 1 1 1 [ 2] 2 1 ( ) ( )( ); 2 D i j ji T i j i j i j J tr          ΣΣ ΣΣ I μμ Σ Σ μμ 1 ( )( ) ; T D ij ij M J J     μ μ Σμ μ Mahalanobis 距离的平方 在协方差矩阵相等条件下散度与 Jd 很相 似，都是对样本在特征空间分散程度的描述。 11 7.4.1 常用的概率距离度量  正态分布下的 Bhattacharyya 距离  如果两类协方差矩阵相等，则 1 1/2 1 () () 8 2 1 |( )/2| ln ; 2 | || | T i j B i j i j i j i j J                 Σ Σ μμ μ μ Σ Σ Σ Σ 1 8( )( ) . T B ij ij DM J J J     μ μ Σμ μ 12 7.4.2 概率距离判据下的特征提取  基本方法：类似于距离度量下的特征提取  设 求映射后的判据表达式（JB, JC, JD）对 A 的各分 量的偏导数并令其为零，得到所需的方程式组， 然后用相应方法求解。  注意：原空间中一个矩阵 W 经映射后变为 , T y Ax  .  T W A WA 

7.4.2概率距离判据下的特征提取 7.4.2概率距离判据下的特征提取 口讨论： 两类别问题，正态分布及相同的协方差阵 口讨论：两类别问题，正态分布及相同的协方差阵 J。=(4-2)2-(1-2) ■设矩阵(AT∑A)-IATMA的特征值矩阵与特征向量 =r[2-4,-,-4,] 矩阵分别是A和U,即有 =r[M(其中，M=(u-2-42)）): (AA)"(AMA)U=UA: →ΣMAU-AUA=0 w-' (具有非奇异变换不变性) 令B=AU,则B是ΣM的特征向量矩阵： A(A)(AMA)(AA)"2MA(AEA)0 对于两类别问题，ramkΣlM=1,即MA=A, MA-EA(AEA)(AMA)=0. (H-2),-μ2)A=A→A=041-2) 7.5基于熵函数的可分性判决 7.5基于熵函数的可分性判决 口熵：事件不确定性的度量 口熵函数： H=J.[P(@lx)...P(@.lx) ■A事件的不确定性大（熵大），则对A事件的 观察所提供的信息量大。 规一化 很 口思路： 0sPs很} ■把各类ω，看作一系列事件，把后验概率P(ωx) 看作特征x上出现o,的概率； ②对称性 J(E.…,P)mJ(P..P) 性 ■如从x能确定⊙，；则对⊙，的观察不提供信息 质 确定性 /00….0)=J0,1….0=…=0 量，熵为0→特征x有利于分类； ④扩张性 J,(…,e)=J(,P0 ■如从x完全不能确定0，，则对0，的观察信息量 大，熵大→特征x无助于分类。 5连续性 P。,)的连续通数 份分枝性（综合性） 一分为二，则熵增加：二合为一，则熵减小 17 7.5基于熵函数的可分性判决 7.5.1基于判别熵最小化的特征提取 口常用的熵函数： 口相对熵：表示某一种分布偏离给定标准分布的程 ■Shannon捕：H=-∑Pa,Ix)logP(alx 度，两种分布重合时最大(0)， r(p,9)=-∑pk)logP2s0 ■平方熵： =2-2PoI四 q飞) 口熵可分离性判据： 口判别熵：表示两类分布之间的差别 J.=∫H(x)px) W(p,q)=V(p.q)+V(q.p) ■J大，则不同类样本重叠性大，可分性不好； =-∑px,)log p(x,)-∑q(x,)logq,) ■J小，则可分性好。 +∑p(3,)log9x,)+∑9s,)logp(x,方

13 7.4.2 概率距离判据下的特征提取  讨论：两类别问题，正态分布及相同的协方差阵   1 12 12 1 1 21 2 1 1 21 2 ( )( ) ( )( ) ( )( ) T D T T J tr tr                   μ μ Σμ μ Σμ μμ μ Σ M M 其中， ； μμμμ             1 1 1 1 1 ( ) ( ) 2 0; 2 0 D T TT T T T D T T J tr J                    A A ΣA A MA A ΣA A Σ M A A MA A A ΣA ΣA MA A ΣA A A ΣA A MA （具有非奇异变换不变性） 14 7.4.2 概率距离判据下的特征提取  讨论：两类别问题，正态分布及相同的协方差阵  设矩阵 (ATΣA)-1ATMA 的特征值矩阵与特征向量 矩阵分别是 Λ 和 U，即有    1 ; T T  A ΣA A MA U U Λ ; =  -1 -1 Σ MAU - AUΛ = 0 令 ，则 是 的特征向量矩阵； B AU B Σ M   1 21 2 1 2 1 ( )( ) . ( ) T rank         -1 -1 -1 -1 Σ M Σ MA = A Σμ μ μ μ A A A Σ μ μ 对于两类别问题， 即 ， ， 15 7.5 基于熵函数的可分性判决  熵：事件不确定性的度量  A 事件的不确定性大（熵大），则对 A 事件的 观察所提供的信息量大。  思路：  把各类ωi 看作一系列事件，把后验概率P(ωi | x) 看作特征 x 上出现ωi 的概率；  如从 x 能确定ωi ，则对ωi 的观察不提供信息 量，熵为0  特征 x 有利于分类；  如从 x 完全不能确定ωi ，则对ωi 的观察信息量 大，熵大  特征 x 无助于分类。 16 7.5 基于熵函数的可分性判决  熵函数：   ( | ), , ( | ) ; 1 x x c P P c H  J    性 质 17 7.5 基于熵函数的可分性判决  常用的熵函数：  Shannon 熵：  平方熵：  熵可分离性判据：  Je大，则不同类样本重叠性大，可分性不好；  Je小，则可分性好。 1 2 1 ( | )log ( | ); c ci i i HP P      x x 2 2 1 21 ( | ). c c i i H P            x ( ) ( ) ,  Je  H x p x dx 18 7.5.1 基于判别熵最小化的特征提取  相对熵：表示某一种分布偏离给定标准分布的程 度，两种分布重合时最大（0），  判别熵：表示两类分布之间的差别 ( ) ( , ) ( )log 0; ( ) i i i p V pq p q    x x x (,) (,) (, ) ( )log ( ) ( )log ( ) ( )log ( ) ( )log ( ); i i ii ii i i W pq V pq Vqp p p qq pq qp           xx xx xx xx

7.5.1基于判别熵最小化的特征提取 7.6PCA特征提取方法与KL变换 口为方便计算，判别熵可被代替 口PCA(Principle Component Analysis)方法： Up,q)=-∑(p-9,)2≤0， 进行特征降维变换，不能完全地表示原有的对 象，能量总会有损失。希望找到一种能量最为集 口目标： 中的的变换方法使损失最小。 minw(p,9)）→minU(p,9)=-∑(p,-g,}≤0 ■通过变换，用较少的特征(，乃，y》近似表示 原来的对象x=(,,…,x}(m<m),并且使 口结论：使U最小的坐标系统（变换矩阵）是由 得误差尽可能的小 矩阵A=G).G2)的前d个（按特征值平方大小） 口K-L(Karhunen-Loeve)变换：最优正交线性变 特征向量组成的，其中G四)、G2是两类各自的协 换，相应的特征提取方法被称为PCA方法。 方差矩阵（估计）。 7.6PCA特征提取方法与K-L变换 7.6PCA特征提取方法与KL变换 口正交变换 口误差 ■给定n维空间中的一组标准正交基真，4，， ■用m个分量表示带来的误差 它诱导了一个线性变换： L:x→yL(☒)=y=04h,…,y) △m)=-豆A产豆 y=x4,i=12,,n, 。目标：误差平方的期望最小 x=乞y4,正交展开· c=[mf]=[交] ■反之，任何一个正交变换也确定了一组正交基。 7.6PCA特征提取方法与K-L变换 7.6PCA特征提取方法与KL变换 口求解最小均方误差正交基： 口求解最小均方误差正交基： ■首先假定随机特征向量为零均值（期望）的，否 ■目标函数：对于一个固定的m 则减掉均值即可 Ex=0; mine,'(m)=minE Σ=E(xx),1 ■找n个正交基4,4，，p,使得对任意一组正交 的协方差矩阵 基，2，…，9a,和所有的m≤n, =m =[2]se=之] s1.l=l,i=m+l,m+2,,m;

19  为方便计算，判别熵可被代替  目标：  结论：使 U 最小的坐标系统（变换矩阵）是由 矩阵 A = G(1)- G(2) 的前 d 个（按特征值平方大小） 特征向量组成的，其中G(1)、G(2)是两类各自的协 方差矩阵（估计）。 7.5.1 基于判别熵最小化的特征提取 2 ( , ) ( ) 0; i i i U pq p q     20 7.6 PCA 特征提取方法与K-L变换  PCA (Principle Component Analysis) 方法： 进行特征降维变换，不能完全地表示原有的对 象，能量总会有损失。希望找到一种能量最为集 中的的变换方法使损失最小。  通过变换，用较少的特征 近似表示 原来的对象 (m<<n)，并且使 得误差尽可能的小。  K-L (Karhunen-Loeve) 变换：最优正交线性变 换，相应的特征提取方法被称为 PCA 方法。 21 7.6 PCA 特征提取方法与K-L变换  正交变换  给定 n 维空间中的一组标准正交基 它诱导了一个线性变换：  反之，任何一个正交变换也确定了一组正交基。 , , , , 1 2  n , 正交展开。 , 1,2, , , : ( ) ( , , , ) , 1 1 2        n i i i i T i T n y y i n L L y y y   x x x y x y   22 7.6 PCA 特征提取方法与K-L变换  误差  用 m 个分量表示带来的误差  目标：误差平方的期望最小 ( ) ; 1 1          n i m i i m i i i x m x y  y  2 2 2 1 () () , n i i m em E m E y               x  23 7.6 PCA 特征提取方法与K-L变换  求解最小均方误差正交基：  首先假定随机特征向量为零均值（期望）的，否 则减掉均值即可  找 n 个正交基 使得对任意一组正交 基 和所有的 m≤n， , , , , 1 2  n 1 2 ,,,,     n    2 2 2 2 1 1 () () ; n n T T i i im im em E em E                    x x Ex  0; 24 7.6 PCA 特征提取方法与K-L变换  求解最小均方误差正交基：  目标函数：对于一个固定的 m     2 1 1 2 min ( ) min min , . . 1, 1, 2, , ; n T T i i i m n T i i i m i em E st im m n                        xx Σ  Σ＝E(xxT)，x 的协方差矩阵

7.6PCA特征提取方法与K-L变换 7.6PCA特征提取方法与KL变换 口求解最小均方误差正交基： 口协方差矩阵的所有特征根是实数，特征向量 a用Lagrange乘子法 也是实的，所有n个特征向量构成一组标准 80-2w2 2[%-奶 正交基，记作，5，…，5m,分别对应特征根 12132…210, 令@=0,1=m+1,m 8o =(51,52，…，5 52 →卫4=，4，i=m+l,…,m →·是Σ的特征向量，乃，是特征根： 口选择协方差矩阵的特征向量乐，5，“，5。作为正 且i侧-三w2)-三4 交基，可以使得均方误差最小。 7.6PCA特征提取方法与K-L变换 7.6PCA特征提取方法与KL变换 口总结 口特征向量常被叫做“主分量”，每个样本被它在前 ■当取协方差矩阵∑的m个最大特征值对应的特征 几个主分量上的投影近似表示 向量来展开飞时，此时的截断均方误差最小。这 m个特征向量组成的正交坐标系称作x所在的n -立6立城-2 维空间的m维Karhunen-Loeve(K-L)变换坐标 系，x在K-L坐标系上的展开系数向量y称作x 口特征值标记着相应特征向量上的能量： 的K-L变换。 口，52，…，5张成的空间称为原空间的子空间， ■实际应用中，协方差矩阵是未知的，用样本协方 PCA实际上是在子空间上的投影，并且 差矩阵代替。 kxf-空6-立空-2 7.6PCA特征提取方法与K-L变换 7.6PCA特征提取方法与KL变换 口KL变换的性质 口例子 。变换后空间中的各特征是互不相关的 E[yy,]=E[5xx'5,]=,5H5,=,6m, E[yy]=E[E'xx'E] =ξ725=A; K-L坐标系把矩阵∑对角化，即通过KL变换 消除原有向量x的各分量间的相关性，从而有可 能去掉那些带有较少信息的分量以达到降低特征 维数的目的

25 7.6 PCA 特征提取方法与K-L变换  求解最小均方误差正交基：  用 Lagrange 乘子法    1 1 () 1 ; n n T T i i i ii im im g                Σ   2 1 1 ( ) 0, 1, , , , 1, , ; () . T i i ii i i n n ii i im im g im n im n e m                        Σ Σ Σ   令 是 的特征向量， 是特征根； 且， 26 7.6 PCA 特征提取方法与K-L变换  协方差矩阵的所有特征根是实数，特征向量 也是实的，所有 n 个特征向量构成一组标准 正交基，记作 分别对应特征根  选择协方差矩阵的特征向量 作为正 交基，可以使得均方误差最小。 1 2 ,,,, n     1 2 ,      n   , , , . 2 1 2 1 1 2                               T n T T n n             1 2 ,,, m     27 7.6 PCA 特征提取方法与K-L变换  总结  当取协方差矩阵Σ的 m 个最大特征值对应的特征 向量来展开 x 时，此时的截断均方误差最小。这 m 个特征向量组成的正交坐标系称作 x 所在的 n 维空间的 m 维 Karhunen-Loeve (K-L) 变换坐标 系，x 在 K-L 坐标系上的展开系数向量 y 称作 x 的 K-L 变换。  实际应用中，协方差矩阵是未知的，用样本协方 差矩阵代替。 28 7.6 PCA 特征提取方法与K-L变换  特征向量常被叫做“主分量”，每个样本被它在前 几个主分量上的投影近似表示  特征值标记着相应特征向量上的能量；  张成的空间称为原空间的子空间， PCA 实际上是在子空间上的投影，并且   ; 1 1 1          m i i i T m i i i n i i i x y  y  x   1 2 ,,, m     2 2 2 12 1 2 1 2 11 11 . n n mm ii ii ii ii ii ii yy yy      x x       29 7.6 PCA 特征提取方法与K-L变换  K-L 变换的性质  变换后空间中的各特征是互不相关的 K-L 坐标系把矩阵Σ对角化，即通过 K-L 变换 消除原有向量 x 的各分量间的相关性，从而有可 能去掉那些带有较少信息的分量以达到降低特征 维数的目的。 , ; TT T i j i j i i j i ij T TT T E yy E E E                         x x y y ξ x x ξ ξ Σξ Λ 1 2 0 ; 0 d           Λ  30 7.6 PCA 特征提取方法与K-L变换  例子