
(四)多元函数积分学 1.理解二重积分、三重积分的概念,了解重积分的性质。 2.掌握二重积分的计算方法(直角坐标、极坐标),了解三重积分的计算方法直角坐标、柱面坐 标、球面坐标)。 3.理解两类曲线积分的概念,了解两类曲线积分的性质及两类曲线积分的关系。 4.会计算两类曲线积分。 5.掌握格林(Green)公式,会使用平面曲线积分与路径无关的条件。 6.了解两类曲面积分的概念及高斯(Guass)斯托克斯(Stokes)公式并会计算两类曲面积分。 7.了解散度、旋度的计算公式。 8.会用重积分、曲线积分及曲面积分求一些几何量与物理量(如体积、曲面面积、弧长、质量、 重心、转动惯量、引力、功等)。 (五)无穷级数 1.理解无穷级数收敛、发散以及和的概念,了解无穷级数基本性质及收敛的必要条件。 2.掌握几何级数和p级数的收敛性。 3.了解正项级数的比较判别法,掌握正项级数的比值判别法。 4.了解交错级数的莱布尼兹判别法,会估计交错级数的截断误差。 5.了解无穷级数绝对收敛与条件收敛的概念以及绝对收敛与收敛的关系。 6.了解函数项级数的收敛域及和函数的概念。 7.掌握比较简单的幂级数收敛区间的求法(区间端点的收敛性可不作要求). 8.了解幂级数在其收敛区间内的一些基本性质。 9.了解函数展开为泰勒级数的充分必要条件。 10会利用c,sinx,cosx-1n(x任x的马克劳林curin)展开式将一些简单的 函数间接展开成幂级数。 11.了解幂级数在近似计算上的简单应用。 I2.了解函数展开为傅里叶(Fourier)级数的狄利克雷(Dirichlet)条件,会将定义在(一π,π)和 (-1,)上的函数展开为傅里叶级数,并会将定义在(0,)上的函数展开为正弦或余弦级数。 说明:教学要求较高的内容用“理解”、“掌握”、“熟悉”等词表述,要求较低的内容用“了解” “会”等词表述
19 (四)多元函数积分学 1. 理解二重积分、三重积分的概念,了解重积分的性质。 2. 掌握二重积分的计算方法(直角坐标、极坐标),了解三重积分的计算方法(直角坐标、柱面坐 标、球面坐标)。 3. 理解两类曲线积分的概念,了解两类曲线积分的性质及两类曲线积分的关系。 4. 会计算两类曲线积分。 5. 掌握格林(Green)公式,会使用平面曲线积分与路径无关的条件。 6. 了解两类曲面积分的概念及高斯(Guass)、斯托克斯(Stokes)公式并会计算两类曲面积分。 7. 了解散度、旋度的计算公式。 8. 会用重积分、曲线积分及曲面积分求一些几何量与物理量(如体积、曲面面积、弧长、质量、 重心、转动惯量、引力、功等)。 (五)无穷级数 1. 理解无穷级数收敛、发散以及和的概念,了解无穷级数基本性质及收敛的必要条件。 2. 掌握几何级数和 p 级数的收敛性。 3. 了解正项级数的比较判别法,掌握正项级数的比值判别法。 4. 了解交错级数的莱布尼兹判别法,会估计交错级数的截断误差。 5. 了解无穷级数绝对收敛与条件收敛的概念以及绝对收敛与收敛的关系。 6. 了解函数项级数的收敛域及和函数的概念。 7. 掌握比较简单的幂级数收敛区间的求法(区间端点的收敛性可不作要求)。 8. 了解幂级数在其收敛区间内的一些基本性质。 9. 了解函数展开为泰勒级数的充分必要条件。 10. 会利用 1 , sin , cos , , ln(1 ), (1 ) 1 x e x x x x x 的马克劳林(Maclaurin)展开式将一些简单的 函数间接展开成幂级数。 11. 了解幂级数在近似计算上的简单应用。 12. 了解函数展开为傅里叶(Fourier)级数的狄利克雷(Dirichlet)条件,会将定义在 ( , ) 和 ( , ) l l 上的函数展开为傅里叶级数,并会将定义在 (0, )l 上的函数展开为正弦或余弦级数。 说明:教学要求较高的内容用“理解”、“掌握”、“熟悉”等词表述,要求较低的内容用“了解”、 “会”等词表述
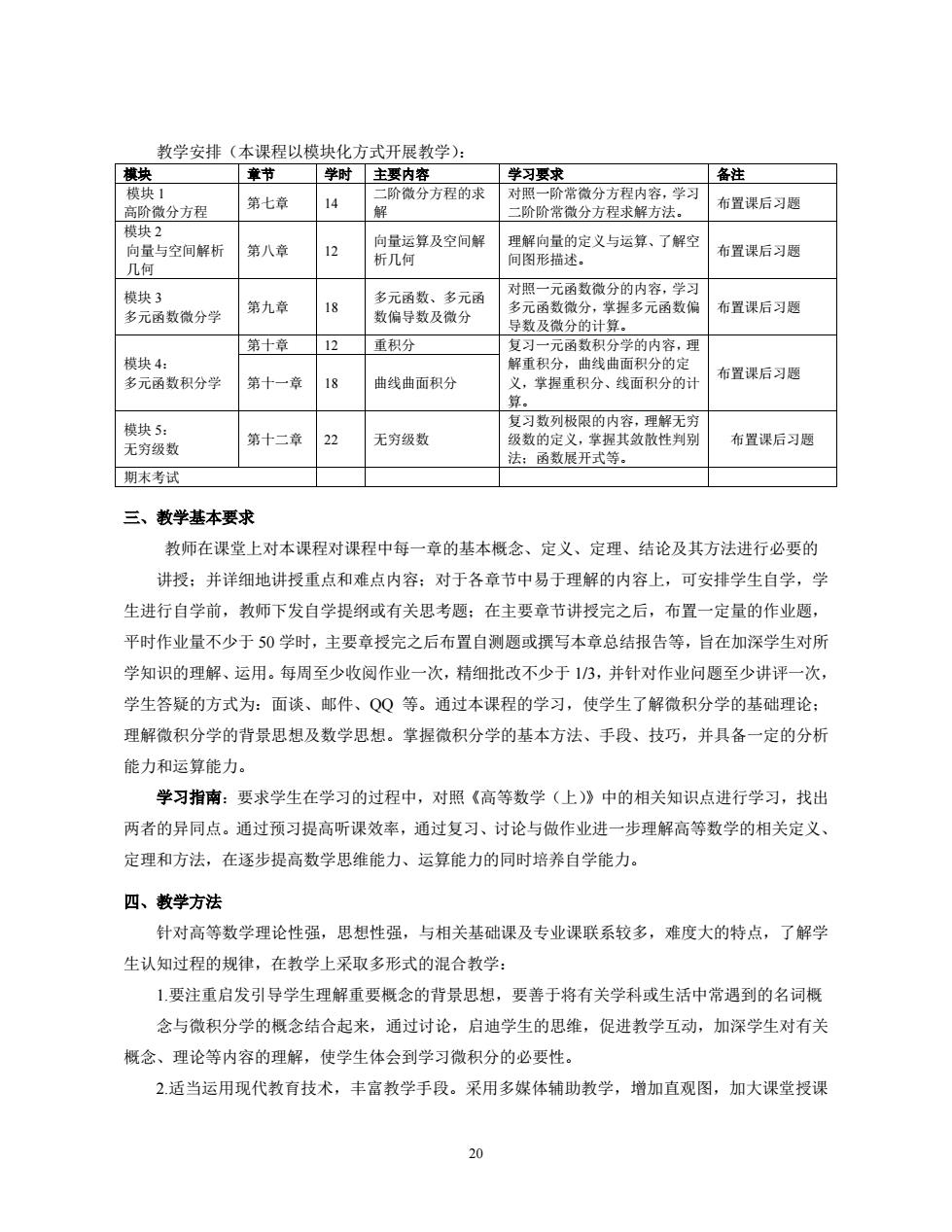
教学安排(本课程以模块化方式开展教学): 章节 学时主要内容 学习要求 备注 第七章 14 微分方程的求 高阶微分方程 ,学习 阶阶常微分方程求解方 布置课后习题 模块2 向量与空间解析 第八意 向量运算及空间解 理解向量的定义与运算、了解空 12 析几何 间图形描述。 布置课后习题 几何 第九章 18 布置课后习题 导数乃尚公的计 第十章 12 重积分 习 元函数积分学的内容,理 模块4: 解重积分,曲线曲面积分的定 多元函数积分学 第十一章 布置课后习题 18 曲线曲面积分 ,掌握重积分、线面积分的计 模块5: ,理解无 无穷级数 第十二章 22 无穷级数 受 布置课后习题 法:函数展开式等。 期末考试 三、教学基本要求 教师在课堂上对本课程对课程中每一章的基本概念、定义、定理、结论及其方法进行必要的 讲授:并详细地讲授重点和难点内容;对于各章节中易于理解的内容上,可安排学生自学,学 生进行自学前,教师下发自学提纲或有关思考题:在主要章节讲授完之后,布置一定量的作业题, 平时作业量不少于50学时,主要章授完之后布置自测题或撰写本章总结报告等,旨在加深学生对所 学知识的理解、运用。每周至少收阅作业一次,精细批改不少于13,并针对作业问题至少讲评一次 学生答疑的方式为:面谈、邮件、QQ等。通过本课程的学习,使学生了解微积分学的基础理论: 理解微积分学的背景思想及数学思想。掌握微积分学的基本方法、手段、技巧,并具备一定的分析 能力和运算能力。 学习指南:要求学生在学习的过程中,对照《高等数学(上)》中的相关知识点进行学习,找出 两者的异同点。通过预习提高听课效率,通过复习、讨论与做作业进一步理解高等数学的相关定义、 定理和方法,在逐步提高数学思维能力、运算能力的同时培养自学能力。 四、教学方法 针对高等数学理论性强,思想性强,与相关基础课及专业课联系较多,难度大的特点,了解学 生认知过程的规律,在教学上采取多形式的混合教学: 1要注重启发引导学生理解重要概念的背景思想,要善于将有关学科或生活中常遇到的名词概 念与微积分学的概念结合起来,通过讨论,启迪学生的思维,促进教学互动,加深学生对有关 概念、理论等内容的理解,使学生体会到学习微积分的必要性。 2.适当运用现代教育技术,丰富教学手段。采用多媒体辅助教学,增加直观图,加大课堂授课
20 教学安排(本课程以模块化方式开展教学): 模块 章节 学时 主要内容 学习要求 备注 模块 1 高阶微分方程 第七章 14 二阶微分方程的求 解 对照一阶常微分方程内容,学习 二阶阶常微分方程求解方法。 布置课后习题 模块 2 向量与空间解析 几何 第八章 12 向量运算及空间解 析几何 理解向量的定义与运算、了解空 间图形描述。 布置课后习题 模块 3 多元函数微分学 第九章 18 多元函数、多元函 数偏导数及微分 对照一元函数微分的内容,学习 多元函数微分,掌握多元函数偏 导数及微分的计算。 布置课后习题 模块 4: 多元函数积分学 第十章 12 重积分 复习一元函数积分学的内容,理 解重积分,曲线曲面积分的定 义,掌握重积分、线面积分的计 算。 布置课后习题 第十一章 18 曲线曲面积分 模块 5: 无穷级数 第十二章 22 无穷级数 复习数列极限的内容,理解无穷 级数的定义,掌握其敛散性判别 法;函数展开式等。 布置课后习题 期末考试 三、教学基本要求 教师在课堂上对本课程对课程中每一章的基本概念、定义、定理、结论及其方法进行必要的 讲授;并详细地讲授重点和难点内容;对于各章节中易于理解的内容上,可安排学生自学,学 生进行自学前,教师下发自学提纲或有关思考题;在主要章节讲授完之后,布置一定量的作业题, 平时作业量不少于 50 学时,主要章授完之后布置自测题或撰写本章总结报告等,旨在加深学生对所 学知识的理解、运用。每周至少收阅作业一次,精细批改不少于 1/3,并针对作业问题至少讲评一次, 学生答疑的方式为:面谈、邮件、QQ 等。通过本课程的学习,使学生了解微积分学的基础理论; 理解微积分学的背景思想及数学思想。掌握微积分学的基本方法、手段、技巧,并具备一定的分析 能力和运算能力。 学习指南:要求学生在学习的过程中,对照《高等数学(上)》中的相关知识点进行学习,找出 两者的异同点。通过预习提高听课效率,通过复习、讨论与做作业进一步理解高等数学的相关定义、 定理和方法,在逐步提高数学思维能力、运算能力的同时培养自学能力。 四、教学方法 针对高等数学理论性强,思想性强,与相关基础课及专业课联系较多,难度大的特点,了解学 生认知过程的规律,在教学上采取多形式的混合教学: 1.要注重启发引导学生理解重要概念的背景思想,要善于将有关学科或生活中常遇到的名词概 念与微积分学的概念结合起来,通过讨论,启迪学生的思维,促进教学互动,加深学生对有关 概念、理论等内容的理解,使学生体会到学习微积分的必要性。 2.适当运用现代教育技术,丰富教学手段。采用多媒体辅助教学,增加直观图,加大课堂授课
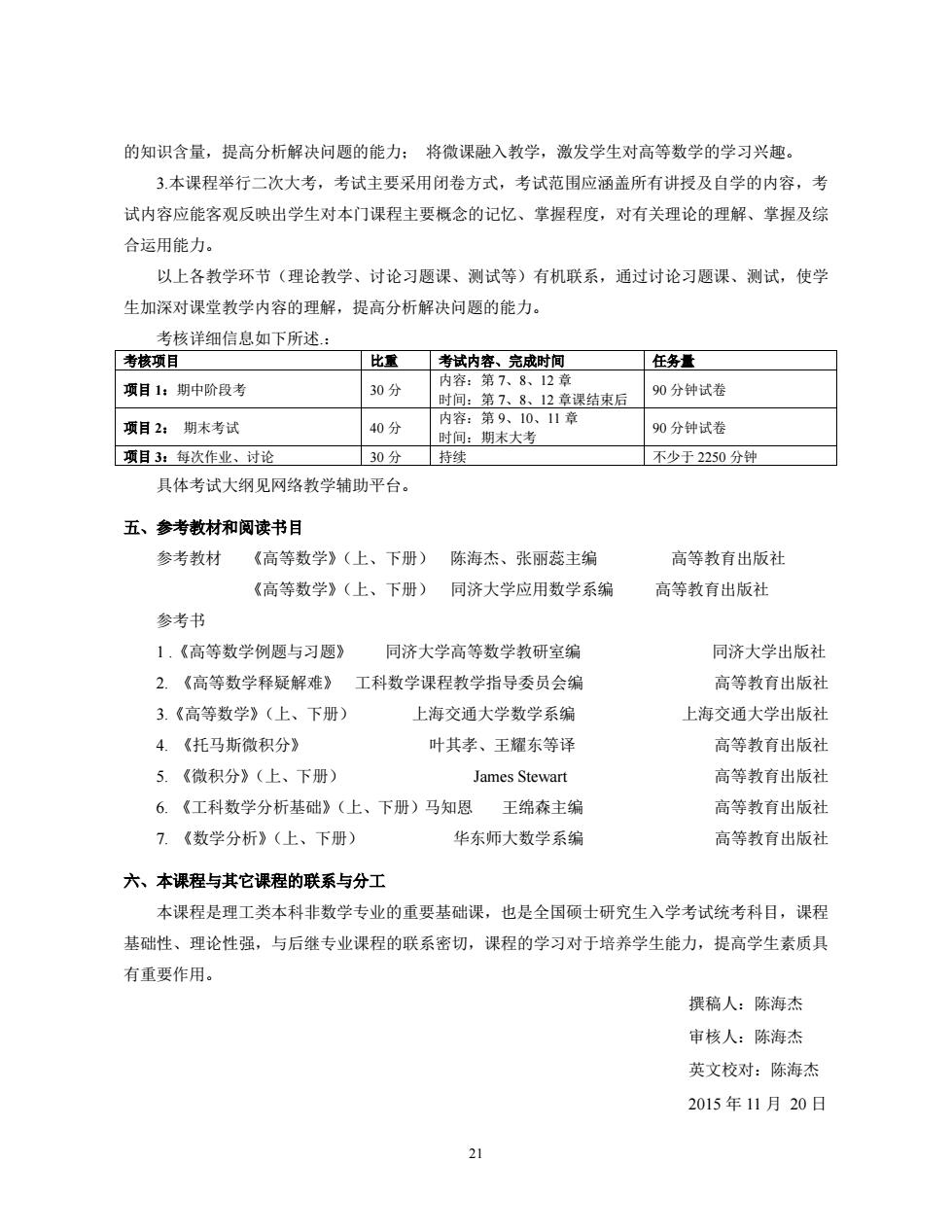
的知识含量,提高分析解决问题的能力:将微课融入教学,激发学生对高等数学的学习兴趣, 3.本课程举行二次大考,考试主要采用闭卷方式,考试范围应涵盖所有讲授及自学的内容,考 试内容应能客观反映出学生对本门课程主要概念的记忆、掌握程度,对有关理论的理解、掌握及综 合运用能力。 以上各教学环节(理论教学、讨论习题课、测试等)有机联系,通过讨论习题课、测试,使学 生加深对课堂教学内容的理解,提高分析解决问题的能力。 考核详细信息如下所述 考核项目 任务量 内 项目1:期中阶段考 30分 时间:第7、8、12章课结束后 90分钟试卷 项目2:期末考试 40分 内容:第9、 90分钟试卷 项目3:每次作业、讨论 30分 持买 不少于2250分钟 具体考试大纲见网络教学辅助平台。 五、参考教材和阅读书目 参考教材 《高等数学》(上、下册)陈海杰、张丽蕊主编 高等教育出版社 《高等数学》(上、下册)同济大学应用数学系编 高等教有出版社 参考书 1.《高等数学例题与习题》 同济大学高等数学教研室编 同济大学出版社 2.《高等数学释疑解难》工科数学课程教学指导委员会编 高等教有出版社 3.《高等数学》(上、下册) 上海交通大学数学系编 上海交通大学出版社 4.《托马斯微积分》 叶其孝、王耀东等译 高等教育出版社 5.《微积分》(上、下册) James Stewart 高等教有出版社 6.《工科数学分析基础》(上、下册)马知恩王绵森主编 高等教育出版社 7.《数学分析》(上、下册) 华东师大数学系编 高等教有出版社 六、本课程与其它课程的联系与分工 本课程是理工类本科非数学专业的重要基础课,也是全国硕士研究生入学考试统考科目,课程 基础性、理论性强,与后继专业课程的联系密切,课程的学习对于培养学生能力,提高学生素质具 有重要作用。 撰稿人:陈海杰 审核人:陈海杰 英文校对:陈海杰 2015年11月20日 之
21 的知识含量,提高分析解决问题的能力; 将微课融入教学,激发学生对高等数学的学习兴趣。 3.本课程举行二次大考,考试主要采用闭卷方式,考试范围应涵盖所有讲授及自学的内容,考 试内容应能客观反映出学生对本门课程主要概念的记忆、掌握程度,对有关理论的理解、掌握及综 合运用能力。 以上各教学环节(理论教学、讨论习题课、测试等)有机联系,通过讨论习题课、测试,使学 生加深对课堂教学内容的理解,提高分析解决问题的能力。 考核详细信息如下所述.: 考核项目 比重 考试内容、完成时间 任务量 项目 1:期中阶段考 30 分 内容:第 7、8、12 章 时间:第 7、8、12 章课结束后 90 分钟试卷 项目 2: 期末考试 40 分 内容:第 9、10、11 章 时间:期末大考 90 分钟试卷 项目 3:每次作业、讨论 30 分 持续 不少于 2250 分钟 具体考试大纲见网络教学辅助平台。 五、参考教材和阅读书目 参考教材 《高等数学》(上、下册) 陈海杰、张丽蕊主编 高等教育出版社 《高等数学》(上、下册) 同济大学应用数学系编 高等教育出版社 参考书 1 .《高等数学例题与习题》 同济大学高等数学教研室编 同济大学出版社 2. 《高等数学释疑解难》 工科数学课程教学指导委员会编 高等教育出版社 3.《高等数学》(上、下册) 上海交通大学数学系编 上海交通大学出版社 4. 《托马斯微积分》 叶其孝、王耀东等译 高等教育出版社 5. 《微积分》(上、下册) James Stewart 高等教育出版社 6. 《工科数学分析基础》(上、下册)马知恩 王绵森主编 高等教育出版社 7. 《数学分析》(上、下册) 华东师大数学系编 高等教育出版社 六、本课程与其它课程的联系与分工 本课程是理工类本科非数学专业的重要基础课,也是全国硕士研究生入学考试统考科目,课程 基础性、理论性强,与后继专业课程的联系密切,课程的学习对于培养学生能力,提高学生素质具 有重要作用。 撰稿人:陈海杰 审核人:陈海杰 英文校对:陈海杰 2015 年 11 月 20 日

《高等数学B(上)》教学大纲 课程名称(中文/英文):高等数学B(上)(Advanced Mathematics B(I) 课程编号:1101443 学分:5分 学时:总学时80 学时分配:讲授学时:80 课程负责人:刘明华 一、课程简介(introduction) 本课程是专为生物、化学、农学、食品等专业的学生而开设。为他们在将来的专业学习、研究 和应用中打下牢固的数学基础。 Advanced Mathematics B is designed to serve students majoring in bioscience,chemical science, agriculture science and food science.It gives students the solid math base they need to succeed in their special study,research and application in the future. 二、教学内容 本科程的研究对象是一元函数(变化过程中量的依赖关系)。内容包括函数、极限、连续,一元 函数微积分学,常微分方程等。通过本课程的学习,要使学生掌握微积分学的基本概念、基本理论 和基本运算技能,为学习后继课程和进一步获得数学知识奠定必要的数学基础。要通过各个教学环 节逐步培养学生的抽象思维能力、逻辑推理能力和自学能力,还要特别注意培养学生的熟练运算能 力和综合运用所学知识去分析解决问题的能力。 (一)函数、极限、连续 1理解函数的概念及函数的奇偶性、单调性、周期性和有界性。 2理解复合函数和反函数的概念。 3.熟悉基本初等函数的性质及其图形。 4.会建立简单实际问题中的函数关系式。 5.理解极限的概念(对极限的£N、£.6定义可在学习过程中逐步加深理解,对于给出£求N或 δ不作过高的要求。),掌握极限四则运算法则及换元法则。 6理解极限存在的夹通准则,了解单调有界准则,会用两个重要极限求极限。 7了解无穷小、无穷大以及无穷小的阶的概念。会用等价无穷小求极限。 8理解函数在一点连续和在一个区间上连续的概念,了解间断点的概念,并会判别间断点的类 2
22 《高等数学 B(上)》教学大纲 课程名称(中文/英文):高等数学 B(上)(Advanced Mathematics B(Ⅰ)) 课程编号:1101443 学 分:5 分 学 时:总学时 80 学时分配:讲授学时:80 课程负责人:刘明华 一、课程简介(introduction) 本课程是专为生物、化学、农学、食品等专业的学生而开设。为他们在将来的专业学习、研究 和应用中打下牢固的数学基础。 Advanced Mathematics B is designed to serve students majoring in bioscience, chemical science, agriculture science and food science. It gives students the solid math base they need to succeed in their special study ,research and application in the future. 二、教学内容 本科程的研究对象是一元函数(变化过程中量的依赖关系)。内容包括函数、极限、连续,一元 函数微积分学,常微分方程等。通过本课程的学习,要使学生掌握微积分学的基本概念、基本理论 和基本运算技能,为学习后继课程和进一步获得数学知识奠定必要的数学基础。要通过各个教学环 节逐步培养学生的抽象思维能力、逻辑推理能力和自学能力,还要特别注意培养学生的熟练运算能 力和综合运用所学知识去分析解决问题的能力。 (一)函数、极限、连续 1.理解函数的概念及函数的奇偶性、单调性、周期性和有界性。 2.理解复合函数和反函数的概念。 3.熟悉基本初等函数的性质及其图形。 4.会建立简单实际问题中的函数关系式。 5.理解极限的概念(对极限的 -N、 - 定义可在学习过程中逐步加深理解,对于给出 求 N 或 不作过高的要求。),掌握极限四则运算法则及换元法则。 6.理解极限存在的夹逼准则,了解单调有界准则,会用两个重要极限求极限。 7.了解无穷小、无穷大以及无穷小的阶的概念。会用等价无穷小求极限。 8.理解函数在一点连续和在一个区间上连续的概念,了解间断点的概念,并会判别间断点的类

型。 9.了解初等函数的连续性和闭区间上连续函数的性质(介值定理和最大、最小值定理) (二)一元函数微分学 1.理解导数和微分的概念,理解导数的几何意义及函数的可导性与连续性之间的关系。会用导 数描述一些物理量 2.掌握导数的四则运算法则和复合函数的求导法,掌握基本初等函数导数公式。了解微分的四 则运算法则和一阶微分形式不变性。 3.了解高阶导数的概念。 4.掌握初等函数一阶、二阶导数的求法。 5.会求隐函数和参数式所确定的函数的一阶、二阶导数。会求反函数的导数。 6.理解罗尔(Role)定理和拉格朗日Lagrange))定理,了解柯西(Cauchy)定理和泰勒(Taylor)定理。 7.会用洛必达L'Hospital)法则求不定式的极限。 8.理解函数的极值概念,掌握用导数判断函数的单调性和求极值的方法。会求解较简单的最大 值和最小值的应用问题。 9.会用导数判断函数图形的凹凸性,会求拐点,会描绘函数的图形(包括水平和铅直渐进线)。 10.了解有向弧与弧微分的概念。了解曲率和曲率半径的概念并会计算曲率和曲率半径。 (三)一元函数积分学 1.理解原函数与不定积分的概念及性质。掌握不定积分的基本公式、换元法和分部积分法。 2.理解定积分的概念及性质,了解可积条件。会求简单的有理函数的积分。 3.理解变上限的积分作为其上限的函数及其求导定理,掌握牛顿Newton)莱布尼兹(Leibniz)公 式。 4.掌握定积分的换元法和分部积分法。 5.了解广义积分的概念以及广义积分的换元法和分部积分法。 6.掌握用定积分表达一些几何量与物理量(如面积、体积、弧长、功、引力等)的方法。 (四)常徽分方程 1.了解微分方程、解、阶、通解、初始条件和特解等概念。 2.掌握变量可分离的方程及一阶线性方程的解法。会解齐次方程和伯努利(Bernoulli)方程,了 解用变量代换求方程的思想。 说明:教学要求较高的内容用“理解”、“掌握”、“熟悉”等词表述,要求较低的内容用“了解” “会”等词表述。 23
23 型。 9.了解初等函数的连续性和闭区间上连续函数的性质(介值定理和最大、最小值定理)。 (二)一元函数微分学 1. 理解导数和微分的概念,理解导数的几何意义及函数的可导性与连续性之间的关系。会用导 数描述一些物理量。 2. 掌握导数的四则运算法则和复合函数的求导法,掌握基本初等函数导数公式。了解微分的四 则运算法则和一阶微分形式不变性。 3. 了解高阶导数的概念。 4. 掌握初等函数一阶、二阶导数的求法。 5. 会求隐函数和参数式所确定的函数的一阶、二阶导数。会求反函数的导数。 6. 理解罗尔(Rolle)定理和拉格朗日(Lagrange)定理,了解柯西(Cauchy)定理和泰勒(Taylor)定理。 7. 会用洛必达(L’Hospital)法则求不定式的极限。 8. 理解函数的极值概念,掌握用导数判断函数的单调性和求极值的方法。会求解较简单的最大 值和最小值的应用问题。 9. 会用导数判断函数图形的凹凸性,会求拐点,会描绘函数的图形(包括水平和铅直渐进线)。 10. 了解有向弧与弧微分的概念。了解曲率和曲率半径的概念并会计算曲率和曲率半径。 (三)一元函数积分学 1. 理解原函数与不定积分的概念及性质。掌握不定积分的基本公式、换元法和分部积分法。 2. 理解定积分的概念及性质,了解可积条件。会求简单的有理函数的积分。 3. 理解变上限的积分作为其上限的函数及其求导定理,掌握牛顿(Newton)-莱布尼兹(Leibniz)公 式。 4. 掌握定积分的换元法和分部积分法。 5. 了解广义积分的概念以及广义积分的换元法和分部积分法。 6. 掌握用定积分表达一些几何量与物理量(如面积、体积、弧长、功、引力等)的方法。 (四)常微分方程 1. 了解微分方程、解、阶、通解、初始条件和特解等概念。 2. 掌握变量可分离的方程及一阶线性方程的解法。会解齐次方程和伯努利(Bernoulli)方程,了 解用变量代换求方程的思想。 说明:教学要求较高的内容用“理解”、“掌握”、“熟悉”等词表述,要求较低的内容用“了解”、 “会”等词表述