C空间格子的4种基本类型(a)原始格子;(b)底心格子(C心);(c)底心格子(A心);(d)底心格子(B心);(e)体心格子;(f)面心格子
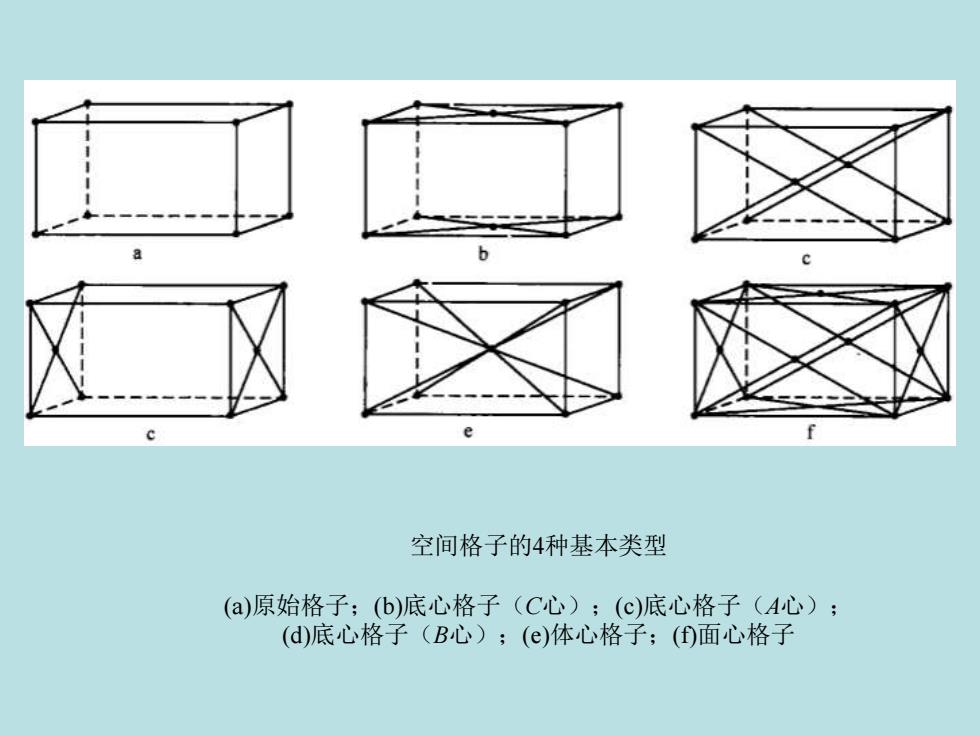
空间格子的4种基本类型 (a)原始格子;(b)底心格子(C心);(c)底心格子(A心); (d)底心格子(B心);(e)体心格子;(f)面心格子

3:十四种布拉维格子按晶格常数7种平行六面体按结点位置4种类型格子是否有7×4=28种空间格子?答案是否定的。因为在这28种中,某些类型的格子彼此重复并可转换,还有一些不符合某晶系的对称特点而不能在该晶系中存在,因此,只有14种空间格子,也叫14种布拉维格子(A.Bravais于1848年最先推导出来的)
3.十四种布拉维格子 按晶格常数——7种平行六面体 按结点位置——4种类型格子 是否有7×4=28种空间格子? 答案是否定的。因为在这28种中,某些类型的格 子彼此重复并可转换,还有一些不符合某晶系的 对称特点而不能在该晶系中存在,因此,只有14 种空间格子,也叫14种布拉维格子。 (A.Bravais于1848年最先推导出来的)

例1:四方底心格子三四方原始格子所以,在14种布拉维格子中,四方底心格子不需要保留
例1:四方底心格子 = 四方原始格子 所以,在14种布拉维格子中,四方底心格子不需要保留
例2:立方底心格子不符合等轴晶系对称特点?因为立方底心格子不具4L3,所以,在14种布拉维格子中,立方底心格子不存在
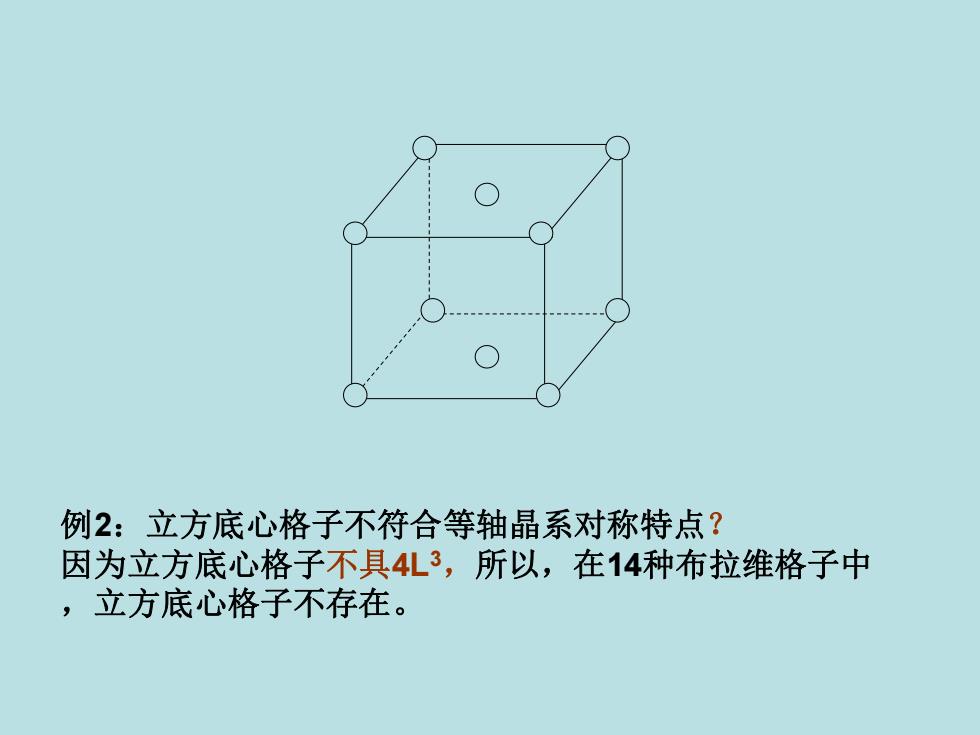
例2:立方底心格子不符合等轴晶系对称特点? 因为立方底心格子不具4L3 ,所以,在14种布拉维格子中 ,立方底心格子不存在