
第8讲状态方程求解 第四章网络分析的状态变量法 《网综》UESTC-陈会主讲
第8讲 状态方程求解 第四章 网络分析的状态变量法 《网综》UESTC-陈会主讲
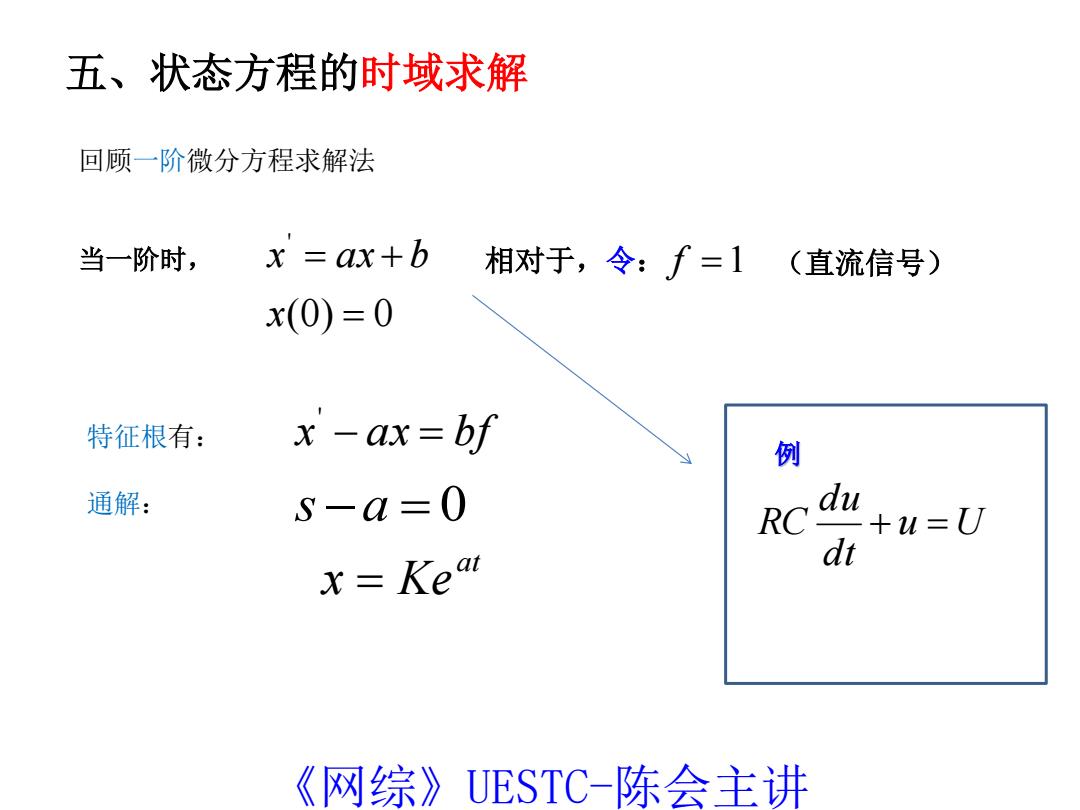
五、状态方程的时域求解 回顾一阶微分方程求解法 当一阶时, x =ax+b 相对于,令:f=1(直流信号) x(0)=0 特征根有: x-ax=bf 例 通解: S-a=0 RC du +u=U x=Kear dt 《网综》UESTC-陈会主讲
五、状态方程的时域求解 x ax bf ' 特征根有: 当一阶时, (0) 0 ' x x ax b at x Ke s a 0 f 1 通解: 相对于,令: 回顾一阶微分方程求解法 (直流信号) u U dt du RC 例 《网综》UESTC-陈会主讲

特解: x=A 代入微分方程 x =ax+b b 可得: A- a 全解: x=Ke ”、b a 因此: 当: b b b K- x(t)= a a a 《网综》UESTC-陈会主讲
ab x Keat 特解 : ab A x A 代入微分方程 全解 : 当: ab K x ( 0 ) 0 因此: ab e ab x t at ( ) x ax b ' 可得: 《网综》UESTC-陈会主讲

思考:状态方程的时域求解? 方程及初始条件: 进一步,1阶微分方程组? x=Ax+Bf x(to)=xo 《网综》UESTC-陈会主讲
0 0 ' x(t ) x x Ax Bf 思考:状态方程的时域求解? 方程及初始条件: 进一步,1阶微分方程组 ? 《网综》UESTC-陈会主讲

换一种方法求1阶微分方程 x =ax+bf x(to)=xo 由参数变易法,令: x(t)=W(t)x (t) 有: x(t)=ax(t)+bf(t) [m(u)xa]=aWx④+bf o品0+xo=awx0+@ a0-ao冰(0=-wo+bfg dt dt 《网综》UESTC-陈会主讲
0 0 ' x(t ) x x ax bf ( ) ( ) ( ) ] ( ) ( ) ( ) [ ( ) ( ) ( ) ( ) ( ) ( ) ( ) [ ( ) ( ) ] ( ) ( ) ( ) ( ) ( ) ( ) 1 1 1 1 1 1 1 b f t d t d x t a W t x t W t d t d W t W t a W t x t b f t d t d x t x t d t d W t W t x t a W t x t b f t d t d x t a x t b f t d t d 换一种方法求1阶微分方程 ( ) ( ) ( ) 1 x t W t x t 有: 由参数变易法,令: 《网综》UESTC-陈会主讲