
第二节空间格子一、空间格子的概念通过上一节的学习,我们已经知道晶体是内部质点呈周期性平移重复排列而具有格子构造的固体。对于大多数晶体而言,由于其内部的质点种类较多,这些质点排列的样式或规律性难以直接观察。为了进一步揭示这种重复规律,我们可以对晶体的结构作某种抽象处理,从而获得一种简单的空间几何图形一一空间格子,这种图形没有物理和化学意义,仅有几何意义,但能够更直观地反映晶体的内部结构,即能够反映组成该晶体质点的排列方式。下面我们以氯化钠晶体为例来介绍这种几何图形的导出过程。在氯化钠的平面结构图[图1-5(a)]中,首先任意选择一个几何点,例如选择某一CI离子中心(选择Na离子中心,或其他位置也可以),然后在结构中找出所有与此点相当的几何点,即相当点(在结构中占据相同的位置且周围环境和位向完全相同的点)。这些点都毫无例外地占据CI离子中心位置,且每一几何点的上、下、左、右必为一Na离子。这样一系列相当点的集合,便构成了一个平面点阵[图1-5(b)1,其中的相当点称为阵点。按照一定法则将这些阵点用直线相连,便能构成一个由平行四边形组成的平面网格图1-5 (c)]。(a)(b)(c)图1-5氯化钠的平面结构图(a)及其导出的平面点阵(b)和平面网格(c)(据李胜荣等,2008)不难想像,在氯化钠的三维结构图(图1-2)中找出来的所有相当点的集合必然构成一个空间点阵,按照一定法则将其阵点用直线相连,便能构成一个由平行六面体共面堆积而成的空间格子。在图O1-2(b)中,若假设选择立方体的8个角项和6个正方形面心的CI离子为相当点,即可得出图1-6所示的空间格子构造(只看上述CI离子的位置,暂时忽略Na离子的位置);同样地,如果在图1-2(b)中以Na离子为相当点,同样可以得到与图1-6相同的空间格子构造。因此,不论O开始时的那个点选在哪里(如假定CI离子和Na离子之图1-6氯化钠的空间格子间的任意一点为相当点),由其相当点构成的空间点阵必·8·
·8· 第二节 空间格子 一、空间格子的概念 通过上一节的学习,我们已经知道晶体是内部质点呈周期性平移重复排列而具有格子 构造的固体。对于大多数晶体而言,由于其内部的质点种类较多,这些质点排列的样式或 规律性难以直接观察。为了进一步揭示这种重复规律,我们可以对晶体的结构作某种抽象 处理,从而获得一种简单的空间几何图形——空间格子,这种图形没有物理和化学意义, 仅有几何意义,但能够更直观地反映晶体的内部结构,即能够反映组成该晶体质点的排列 方式。下面我们以氯化钠晶体为例来介绍这种几何图形的导出过程。 在氯化钠的平面结构图[图 1-5(a)]中,首先任意选择一个几何点,例如选择某一 Cl- 离子中心(选择 Na+ 离子中心,或其他位置也可以),然后在结构中找出所有与此点相当的 几何点,即相当点(在结构中占据相同的位置且周围环境和位向完全相同的点)。这些点都 毫无例外地占据 Cl-离子中心位置,且每一几何点的上、下、左、右必为一 Na+ 离子。这 样一系列相当点的集合,便构成了一个平面点阵[图 1-5(b)],其中的相当点称为阵点。按 照一定法则将这些阵点用直线相连,便能构成一个由平行四边形组成的平面网格[图 1-5(c)]。 (a) (b) (c) 图 1-5 氯化钠的平面结构图(a)及其导出的平面点阵(b)和平面网格(c)(据李胜荣等,2008) 不难想像,在氯化钠的三维结构图(图 1-2)中找出来的所有相当点的集合必然构成一 个空间点阵,按照一定法则将其阵点用直线相连,便能构 成一个由平行六面体共面堆积而成的空间格子。在图 1-2(b)中,若假设选择立方体的 8 个角顶和 6 个正方形面 心的 Cl- 离子为相当点,即可得出图 1-6 所示的空间格子 构造(只看上述 Cl-离子的位置,暂时忽略 Na+离子的位 置);同样地,如果在图 1-2(b)中以 Na+离子为相当点, 同样可以得到与图 1-6 相同的空间格子构造。因此,不论 开始时的那个点选在哪里(如假定 Cl-离子和 Na+离子之 间的任意一点为相当点),由其相当点构成的空间点阵必 图 1-6 氯化钠的空间格子

定也是在三维空间呈周期性重复并能体现氯化钠晶体中CI离子和Na离子的分布规律。显然,对于其他任何晶体,不管其结构如何复杂,只要任意选定一个点并将其所有的相当点找出来,就能得到相应的空间格子,从而揭示其内部质点的重复规律,我们由此可以把握复杂的晶体结构的本质规律,将复杂问题抽象化、简单化。对于同一结构型的晶体而言,所得出的空间点阵应当是完全相同的:而对于不同结构型的晶体而言,所得到的空间格子构造一般是不相同的。综上所述,所谓“空间格子”就是表示晶体内部质点在三维空间作周期性平移重复排列规律的几何图形。空间格子以简捷的形式反映了晶体格子构造的特点,便于研究晶体内部质点的重复规律而不受晶体大小的限制,可以设想空间格子是一种无限图形,其在三维空间的无限延伸即代表了晶体的结构特点,其图1-7:空间格子-般形式如图1-7所示。二、空间格子要素及其基本规律空间格子要素包括结点、行列、面网和平行六面体。各要素的定义、特点及其相互关系遵循以下规律。1.结点结点是空间格子中的点,它们由晶体结构中的相当点构成。需要说明,在空间格子中的结点不代表任何实际的质点,它是仅有几何意义的几何点:而在实际晶体中,相当点既可以代表某一种质点,也可以代表另一种质点或其他一类相当点,例如,NaCI的晶体结构中,相当点既可以代表CI离子,也可以代表Na离子,还可以代表CI离子和Na离子之间的任意点。2.行列分布在同一直线上的结点构成一个行列,可见,空间格子中任意两个结点联结起来就可以决定一条行列。在同一条行列上两个相邻结点之间的距离,称为结点间距a,结点间距反映了质点在该行列方向上的最小重复周期(图1-8)。在一个空间格子中,可以有无穷多不同方向的行列,但同一行列上结点间距相等;彼此平行的行列,其结点间距也必定相等,否则与格子构造的概念相矛盾;不同方向上的行列,结oo点间距可能相等,也可能不相等。由此可见,在某些方向上图1-8空间格子中的行列的行列结点分布较密,而在有些方向上结点分布较稀疏。3.面网结点在同一平面上的分布便构成一个面网。显然,空间格子中不在同一行列的任意3个结点就可以决定一个面网的方向:换言之,任意两个相交的行列可以决定一个面网,如图(图1-9),OA1、OB两个相交的行列构成一个面网。面网上单位面积内结点的数目称为面网密度。任意两个相邻面网之间的垂直距离称为面网间距。在一个空间格子中,可以有无穷多个不同方向的面网,相互平行的面网,其面网密度相等:不同方向的面网,其面网密度一般不相等。面网密度与面网间距之间存在着一定的关系。图1-10为分布在纸平面上的一些结点,.9
·9· 定也是在三维空间呈周期性重复并能体现氯化钠晶体中 Cl- 离子和 Na+ 离子的分布规律。 显然,对于其他任何晶体,不管其结构如何复杂,只要任意选定一个点并将其所有的 相当点找出来,就能得到相应的空间格子,从而揭示其内部质点的重复规律,我们由此可 以把握复杂的晶体结构的本质规律,将复杂问题抽象化、简单化。对于同一结构型的晶体 而言,所得出的空间点阵应当是完全相同的;而对于不同结构型的晶体而言,所得到的空 间格子构造一般是不相同的。 综上所述,所谓“空间格子”就是表示晶体内部 质点在三维空间作周期性平移重复排列规律的几何 图形。空间格子以简捷的形式反映了晶体格子构造的 特点,便于研究晶体内部质点的重复规律而不受晶体 大小的限制,可以设想空间格子是一种无限图形,其 在三维空间的无限延伸即代表了晶体的结构特点,其 一般形式如图 1-7 所示。 二、空间格子要素及其基本规律 空间格子要素包括结点、行列、面网和平行六面体。各要素的定义、特点及其相互关 系遵循以下规律。 1. 结点 结点是空间格子中的点,它们由晶体结构中的相当点构成。需要说明,在空间格子中 的结点不代表任何实际的质点,它是仅有几何意义的几何点;而在实际晶体中,相当点既 可以代表某一种质点,也可以代表另一种质点或其他一类相当点,例如,NaCl 的晶体结构 中,相当点既可以代表 Cl-离子,也可以代表 Na+离子,还可以代表 Cl-离子和 Na+离子之 间的任意点。 2. 行列 分布在同一直线上的结点构成一个行列,可见,空间格子中任意两个结点联结起来就 可以决定一条行列。在同一条行列上两个相邻结点之间的距离,称为结点间距 a,结点间 距反映了质点在该行列方向上的最小重复周期(图 1-8)。在一个空间格子中,可以有无穷 多不同方向的行列,但同一行列上结点间距相等;彼此平行的行列,其结点间距也必定相 等,否则与格子构造的概念相矛盾;不同方向上的行列,结 点间距可能相等,也可能不相等。由此可见,在某些方向上 的行列结点分布较密,而在有些方向上结点分布较稀疏。 3. 面网 结点在同一平面上的分布便构成一个面网。显然,空间格子中不在同一行列的任意 3 个结点就可以决定一个面网的方向;换言之,任意两个相交的行列可以决定一个面网,如 图(图 1-9),OA1、OB1两个相交的行列构成一个面网。面网上单位面积内结点的数目称为 面网密度。任意两个相邻面网之间的垂直距离称为面网间距。在一个空间格子中,可以有 无穷多个不同方向的面网,相互平行的面网,其面网密度相等;不同方向的面网,其面网 密度一般不相等。 面网密度与面网间距之间存在着一定的关系。图 1-10 为分布在纸平面上的一些结点, 图 1-8 空间格子中的行列 图 1-7 空间格子

现垂直于纸平面作不同方向的面网,它们与纸平面的交线分别为AA,BB,CC和DD行列。不难理解,这些行列的结点间距越大,相应面网的面网密度就越小。另外,随着这些行列的结点间距越来越大,它们与某一固定行列AD之间的交角B则越来越小,而相应的面网间距d又与sinβ(i-1,2,3,.)成正比,即d=bo-sinβi式中的b.为行列AD的结点间距,从中可以看出,面网密度越大,相应的面网间距也越大:反之,面网密度越小,相应的面网间距也越小。bDblP,KB,KBR·b.0a44AABCDA图1-9空间格子中的面网图1-10面网密度与面网间距的关系图(据罗谷风,1985)4.平行六面体平行六面体是空间格子中最小的重复单元(图1-11),它由3对两两平行且相等的面组成。整个空c.间格子可以看作是平行六面体在三维空间平行地、毫无间隙地重复累叠而成的。每一平行六面体的3组梭棱长(a,b,c)恰好就是3个相应行列的结点间距,3个棱a.的夹角分别为α,β,,其中a=bcac,ab。7图1-11平行六面体第三节14种布拉维空间格子一、平行六面体的选取原则如前所述,晶体结构的最基本特性是其内部质点在三维空间作有规律的周期性重复;表示晶体结构重复规律性的几何图形称为空间格子。在实际晶体中,晶体结构是由晶体内部的相当点(原子种类相同,原子周围的环境和方位都相同的点)所构成的空间格子在三维空间排列而成。平行六面体是空间格子中的最小重复单元,整个晶体结构可视为是这种平行六面体在三维空间平行的、毫无间隙的重复堆砌而成的。对于特定的晶体结构而言,其对应的空间格子中结点的分布是客观存在的,但平行六面体的选择是人为的。同一种格子构造,其平行六面体的选择可有多种方式(图1-12)。因此,只有遵循一定的平行六面体选取原则,才能得到统一的选择结果。在结晶学中,从空间格子构造中选择平行六面体应遵循以下原则:.10
·10· 现垂直于纸平面作不同方向的面网,它们与纸平面的交线分别为 AA',BB',CC'和 DD' 行列。不难理解,这些行列的结点间距越大,相应面网的面网密度就越小。另外,随着这 些行列的结点间距越来越大,它们与某一固定行列 AD 之间的交角 βi则越来越小,而相应 的面网间距 di 又与 sinβi(i=1,2,3,······)成正比,即 di=b0·sinβi 式中的 b0为行列 AD 的结点间距,从中可以看出,面网密度越大,相应的面网间距也 越大;反之,面网密度越小,相应的面网间距也越小。 图 1-9 空间格子中的面网 图 1-10 面网密度与面网间距的关系图(据罗谷风,1985) 4. 平行六面体 平行六面体是空间格子中最小的重复单元(图 1-11),它由 3 对两两平行且相等的面组成。整个空 间格子可以看作是平行六面体在三维空间平行地、毫 无间隙地重复累叠而成的。每一平行六面体的 3 组棱 长(a,b,c)恰好就是 3 个相应行列的结点间距,3 个棱 的夹角分别为 α,β,γ,其中 α=b∧c,β=a∧c,γ=a∧b。 第三节 14 种布拉维空间格子 一、平行六面体的选取原则 如前所述,晶体结构的最基本特性是其内部质点在三维空间作有规律的周期性重复; 表示晶体结构重复规律性的几何图形称为空间格子。在实际晶体中,晶体结构是由晶体内 部的相当点(原子种类相同,原子周围的环境和方位都相同的点)所构成的空间格子在三维 空间排列而成。平行六面体是空间格子中的最小重复单元,整个晶体结构可视为是这种平 行六面体在三维空间平行的、毫无间隙的重复堆砌而成的。 对于特定的晶体结构而言,其对应的空间格子中结点的分布是客观存在的,但平行六 面体的选择是人为的。同一种格子构造,其平行六面体的选择可有多种方式(图 1-12)。因 此,只有遵循一定的平行六面体选取原则,才能得到统一的选择结果。 在结晶学中,从空间格子构造中选择平行六面体应遵循以下原则: 图 1-11 平行六面体
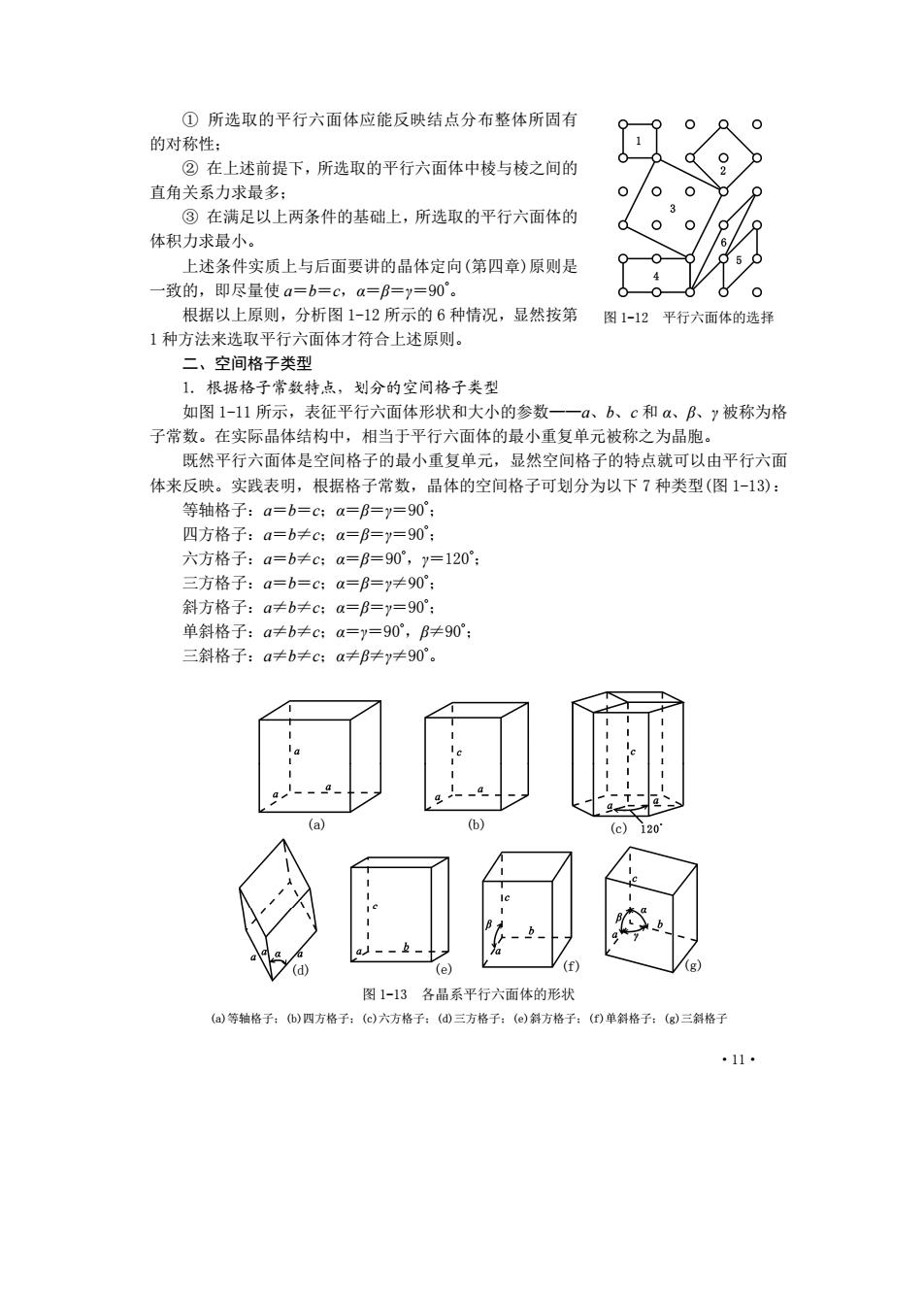
①所选取的平行六面体应能反映结点分布整体所固有O的对称性;②在上述前提下,所选取的平行六面体中棱与棱之间的直角关系力求最多:③在满足以上两条件的基础上,所选取的平行六面体的体积力求最小。上述条件实质上与后面要讲的晶体定向(第四章)原则是一致的,即尽量使a=b=C,α=β==90。C根据以上原则,分析图1-12所示的6种情况,显然按第图1-12平行六面体的选择1种方法来选取平行六面体才符合上述原则。二、空间格子类型1.根据格子常数特点,划分的空间格子类型如图1-11所示,表征平行六面体形状和大小的参数-一a、b、c和α、β、被称为格子常数。在实际晶体结构中,相当于平行六面体的最小重复单元被称之为晶胞。既然平行六面体是空间格子的最小重复单元,显然空间格子的特点就可以由平行六面体来反映。实践表明,根据格子常数,晶体的空间格子可划分为以下7种类型(图1-13):等轴格子:α=b=c;α=β=90°;四方格子:α=b≠c;α=β==90°;六方格子:a=b≠cα=β=90,=120三方格子:a=b=cα=≠90;斜方格子:ab≠c;α=β==90单斜格子:a±b±c;α==90,β±90;三斜格子:a≠bc;α90。(b)2(d)(e)图1-13各晶系平行六面体的形状(a)等轴格子:(b)四方格子:(c)六方格子:(d)三方格子:(e)斜方格子:(f)单斜格子:(g)三斜格子.11
·11· ① 所选取的平行六面体应能反映结点分布整体所固有 的对称性; ② 在上述前提下,所选取的平行六面体中棱与棱之间的 直角关系力求最多; ③ 在满足以上两条件的基础上,所选取的平行六面体的 体积力求最小。 上述条件实质上与后面要讲的晶体定向(第四章)原则是 一致的,即尽量使 a=b=c,α=β=γ=90° 。 根据以上原则,分析图 1-12 所示的 6 种情况,显然按第 1 种方法来选取平行六面体才符合上述原则。 二、空间格子类型 1. 根据格子常数特点,划分的空间格子类型 如图 1-11 所示,表征平行六面体形状和大小的参数——a、b、c 和 α、β、γ 被称为格 子常数。在实际晶体结构中,相当于平行六面体的最小重复单元被称之为晶胞。 既然平行六面体是空间格子的最小重复单元,显然空间格子的特点就可以由平行六面 体来反映。实践表明,根据格子常数,晶体的空间格子可划分为以下 7 种类型(图 1-13): 等轴格子:a=b=c;α=β=γ=90° ; 四方格子:a=b≠c;α=β=γ=90° ; 六方格子:a=b≠c;α=β=90° ,γ=120° ; 三方格子:a=b=c;α=β=γ≠90° ; 斜方格子:a≠b≠c;α=β=γ=90° ; 单斜格子:a≠b≠c;α=γ=90° ,β≠90° ; 三斜格子:a≠b≠c;α≠β≠γ≠90° 。 图 1-13 各晶系平行六面体的形状 (a)等轴格子;(b)四方格子;(c)六方格子;(d)三方格子;(e)斜方格子;(f)单斜格子;(g)三斜格子 图 1-12 平行六面体的选择 (a) (b) (c) (f) (g) (d) (e)

2.根据结点的分布位置,划分的空间格子类型由平行六面体选择原则选出的平行六面体中,结点的分布只能有4种情况,即可划分为以下4种格子类型(图1-14):(a)(b)c(d)(e)(f)图1-14空间格子的4种基本类型(据李胜荣等,2008)(a)原始格子:(b)底心格子(C心):(c)底心格子(A心):(d)底心格子(B心):(e)体心格子:(f)面心格子①原始格子(P)一一结点分布于平行六面体的8个角顶上。②底心格子一一结点分布于平行六面体的角项及某一对面的中心。其中,根据面中心点的位置特点又可细分为:C心格子,即结点分布于平行六面体的角顶和垂直于Z轴的一对面的中心:A心格子,即结点分布于平行六面体的角顶和垂直于X轴的一对面的中心;B心格子,即结点分布于平行六面体的角顶和垂直于Y轴的一对面的中心。底心格子一般情况下指的是C心格子。③体心格子()一一结点分布于平行六面体的角顶和平行六面体中心。④面心格子(F)一一结点分布于平行六面体的角顶和三对面的中心。一般将原始格子看作是平行六面体的基本形式,而将其他3种格子看成是在原始格子的基础上复杂化衍生而成。3.14种布拉维空间格子如上所述,按格子常数(即平行六面体的形状和大小),空间格子分为7种类型:按平行六面体结点的分布情况,空间格子分为4种类型,那么,依据排列组合似乎应该共有28种空间格子。但实际上空间格子并没有那么多,一是因为某些类型的格子彼此重复并可转换,还有一些不符合某晶系的对称特点而不能在该晶系中存在。一些格子可以相互转化,如图1-15所示,四方底心格子转化为四方原始格子,三方面心格子转化为三方原始格子,而且体积变得更小,根据上述的平行六面体选取中的尽量使体积最小的原则,前者为后者替代:有一些不符合晶体对称规律而实际不存在,如等轴晶系中不存在立方底心格子,因为若在立方格子中的一对面的中心安置结点,则完全不符合等轴晶系具4L3的对称特点,因此不可能存在立方底心格子。综合考虑平行六面体的形状及结点的分布情况,在晶体结构中只可能出现14种不同形式的空间格子,这是由布拉维(A.Bravais)于1848年首先推导出来的,故称14种布拉维格子(表1-1)。·12
·12· 2. 根据结点的分布位置,划分的空间格子类型 由平行六面体选择原则选出的平行六面体中,结点的分布只能有 4 种情况,即可划分 为以下 4 种格子类型(图 1-14): (d) (e) (f) 图 1-14 空间格子的 4 种基本类型(据李胜荣等,2008) (a)原始格子;(b)底心格子(C 心);(c)底心格子(A 心);(d)底心格子(B 心);(e)体心格子;(f)面心格子 ① 原始格子(P) —— 结点分布于平行六面体的 8 个角顶上。 ② 底心格子 —— 结点分布于平行六面体的角顶及某一对面的中心。其中,根据面中 心点的位置特点又可细分为:C 心格子,即结点分布于平行六面体的角顶和垂直于 Z 轴的 一对面的中心;A 心格子,即结点分布于平行六面体的角顶和垂直于 X 轴的一对面的中心; B 心格子,即结点分布于平行六面体的角顶和垂直于 Y 轴的一对面的中心。底心格子一般 情况下指的是 C 心格子。 ③ 体心格子(I) —— 结点分布于平行六面体的角顶和平行六面体中心。 ④ 面心格子(F) —— 结点分布于平行六面体的角顶和三对面的中心。 一般将原始格子看作是平行六面体的基本形式,而将其他 3 种格子看成是在原始格子 的基础上复杂化衍生而成。 3. 14 种布拉维空间格子 如上所述,按格子常数(即平行六面体的形状和大小),空间格子分为 7 种类型;按平 行六面体结点的分布情况,空间格子分为 4 种类型,那么,依据排列组合似乎应该共有 28 种空间格子。但实际上空间格子并没有那么多,一是因为某些类型的格子彼此重复并可转 换,还有一些不符合某晶系的对称特点而不能在该晶系中存在。一些格子可以相互转化, 如图 1-15 所示,四方底心格子转化为四方原始格子,三方面心格子转化为三方原始格子, 而且体积变得更小,根据上述的平行六面体选取中的尽量使体积最小的原则,前者为后者 替代;有一些不符合晶体对称规律而实际不存在,如等轴晶系中不存在立方底心格子,因 为若在立方格子中的一对面的中心安置结点,则完全不符合等轴晶系具 4L3 的对称特点, 因此不可能存在立方底心格子。综合考虑平行六面体的形状及结点的分布情况,在晶体结 构中只可能出现 14 种不同形式的空间格子,这是由布拉维(A.Bravais)于 1848 年首先推导 出来的,故称 14 种布拉维格子(表 1-1)。 (a) (b) (c)