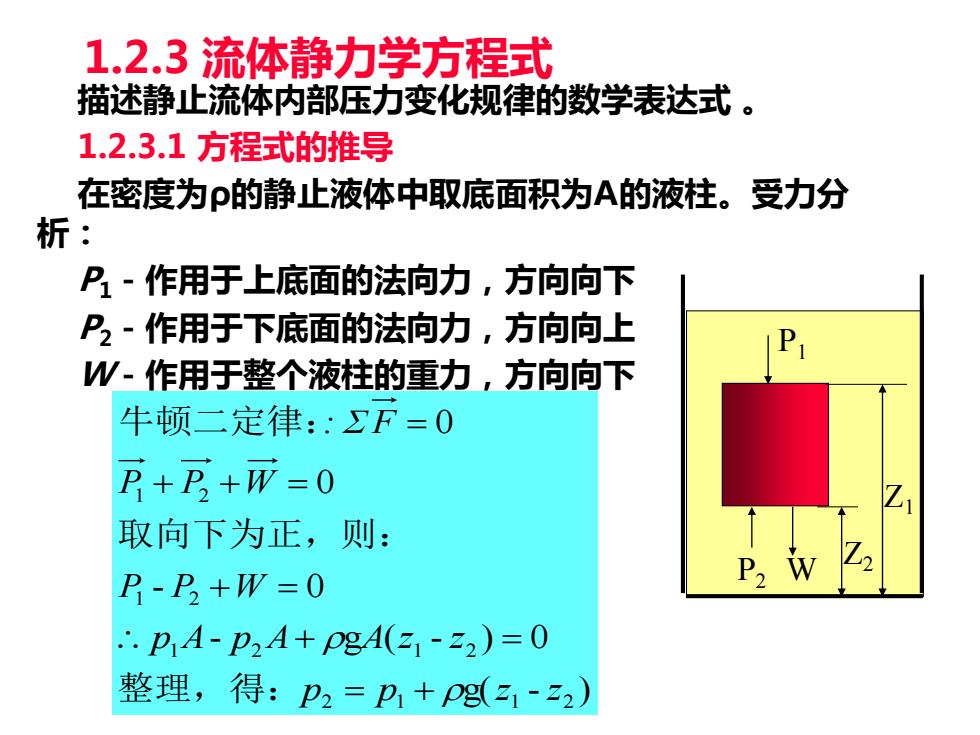
1.2.3流体静力学方程式 描述静止流体内部压力变化规律的数学表达式。 1.2.3.1方程式的推导 在密度为P的静止液体中取底面积为A的液柱。受力分 析: P~作用于上底面的法向力,方向向下 P2~作用于下底面的法向力,方向向上 W-作用于整个液柱的重力,方向向下 牛顿二定律::F=0 F+E+币=0 取向下为正,则: P-P+W-=0 ∴.P1A-p2A+PgA(21-22)=0 整理,得:p2=pP1+Pg(31-2)
1.2.3 流体静力学方程式 描述静止流体内部压力变化规律的数学表达式 。 1.2.3.1 方程式的推导 在密度为ρ的静止液体中取底面积为A的液柱。受力分 析: P1-作用于上底面的法向力,方向向下 P2-作用于下底面的法向力,方向向上 W-作用于整个液柱的重力,方向向下 P1 Z2 P2 W Z1 g( - ) - g ( - ) 0 - 0 0 0 2 1 1 2 1 2 1 2 1 2 1 2 p p z z p A p A A z z P P W P P W : F = + + = + = + + = = 整理,得: 取向下为正,则: 牛顿二定律:

上式可改写为: P2+Pg2五=P1+pgZ1 P2/p+g2五=P1/p+gz P2/pg+2五=P1/pg+z 当取液柱上表面为液面,表面上方压力为P,则液 柱高度为h处压力为:p=Po+pgh 以上几个式子均称为流体静力学基本方程。 流体静力学方程的物理意义: 静止流体内部任一点其总能量是一个常数(ρ的单 位是/m3,p/p的单位是/kg,p/pg的单位是/N) 上式也可改写为:h=(P2·P1)/Pg
上式可改写为: p2 +ρg z2 = p1 +ρg z1 p2 /ρ+g z2 = p1 /ρ+g z1 p2 /ρg+ z2 = p1 /ρg+ z1 当取液柱上表面为液面,表面上方压力为p0 ,则液 柱高度为h处压力为: p=p0+ρgh 以上几个式子均称为流体静力学基本方程。 流体静力学方程的物理意义: 静止流体内部任一点其总能量是一个常数(p的单 位是J/ m3 ,p/ρ的单位是J/kg,p/ρg的单位是J/N) 上式也可改写为: h= (p2 - p1 )/ ρg

反映静止流体内部压力变化规律。 敞口时,P0为大气压;密闭时,P为液体蒸汽压。 1.2.3.2方程式的讨论 1.静止流体内部两点间压力差的大小,只与其垂直 距离和流体的密度有关,而与其水平位置和容器的形状 无关。 2.在静止液体中,当位置1处压力p发生变化时,位 置2处压力P2亦发生同样大小的变化,即压力具有传递 性(在液体中)。 3.当Po=cons时,p↑,pt;hf,p1
反 映 静 止 流 体 内 部 压 力 变 化 规 律 。 敞口时,p0为大气压;密闭时,p0为液体蒸汽压。 1.2.3.2 方程式的讨论 1. 静止流体内部两点间压力差的大小,只与其垂直 距离和流体的密度有关,而与其水平位置和容器的形状 无关。 2.在静止液体中,当位置1处压力p1发生变化时,位 置2处压力p2亦发生同样大小的变化,即压力具有传递 性(在液体中) 。 3.当p0=const时, ρ↑,p↑;h↑,p↑

4.将方程式写成h=(p-P/Pg,知压力差的大 小可用液体柱高度表示,但需注明液体种类。 5.静止、连续的同一流体中,处于同一水平面 上各点的压力相等,称为等压面。 6.对于气体,因密度随所处位置高度而变化 ,该方程式不适用。但在化工容器中这种变化 甚小,故可认为仍然适用,而且近似认为P2=P 7.前述方程式适用场合: 静止、连续、同种流体 相对静止、连续、同种流体
4.将方程式写成h=(p-p0 )/ρg,知压力差的大 小可用液体柱高度表示,但需注明液体种类。 5.静止、连续的同一流体中,处于同一水平面 上各点的压力相等,称为等压面。 6.对于气体,因密度随所处位置高度而变化 ,该方程式不适用。但在化工容器中这种变化 甚小,故可认为仍然适用,而且近似认为p2=p1。 7.前述方程式适用场合: 静止、连续、同种流体 相对静止、连续、同种流体
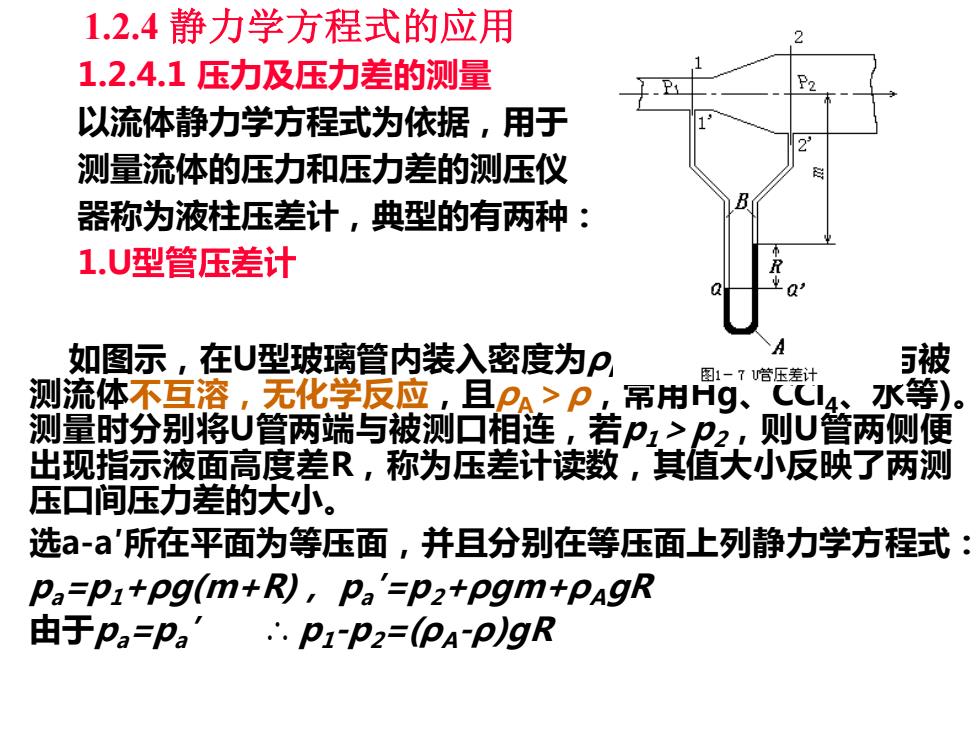
1.2.4静力学方程式的应用 2 1.2.4.1压力及压力差的测量 以流体静力学方程式为依据,用于 测量流体的压力和压力差的测压仪 器称为液柱压差计,典型的有两种: 1.U型管压差计 如图示,在U型玻璃管内装入密度为P 图1-7哈压差计 被 测流体不互溶,无化学反应,且P,>P,吊用Hg、4水等)。 测量时分别将U管两端与被测口相连,若P1>P2,则U管两侧便 出现指示液面高度差R,称为压差计读数,其值大小反映了两测 压口间压力差的大小。 选a-'所在平面为等压面,并且分别在等压面上列静力学方程式: pa=p:+pg(m+R),pa'=p2+pgm+pagR 由于Pa=Pa'∴.P1P2=(OA-p)gR
1.2.4 静力学方程式的应用 1.2.4.1 压力及压力差的测量 以流体静力学方程式为依据,用于 测量流体的压力和压力差的测压仪 器称为液柱压差计,典型的有两种: 1.U 如图示,在U型玻璃管内装入密度为ρA的指示液A(要求A与被 测流体不互溶,无化学反应,且ρA>ρ,常用Hg、CCl4、水等)。 测量时分别将U管两端与被测口相连,若p1>p2,则U管两侧便 出现指示液面高度差R,称为压差计读数,其值大小反映了两测 压口间压力差的大小。 选a-a′所在平面为等压面,并且分别在等压面上列静力学方程式: pa=p1+ρg(m+R), pa ′=p2+ρgm+ρAgR 由于pa=pa ′ ∴ p1-p2=(ρA-ρ)gR