
R S H(jo) H(S)= L R L LO Wo S H(S)= g O-s+0 2s H(s)= 2+2s+10
2 10 2 ( ) 2 s s s H s H( j) 2 0 2 ( ) s Q s s Q H s o o L LC R s s L R s H s 1 ( ) 2
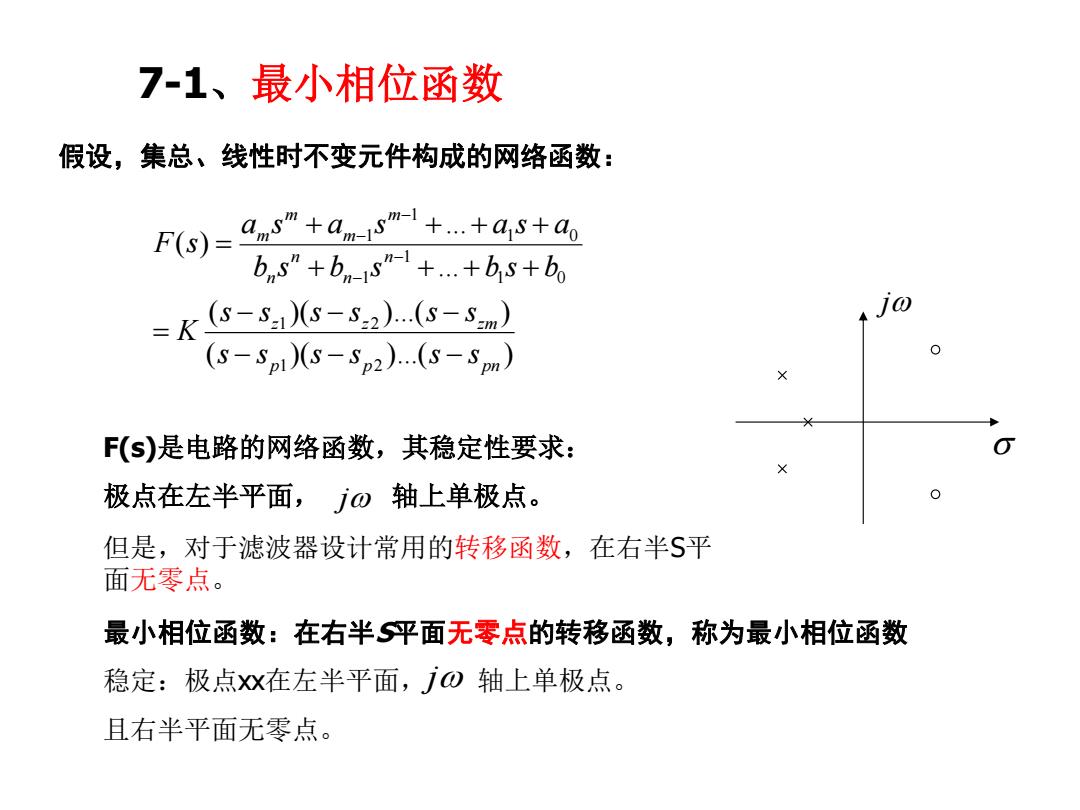
7-1、最小相位函数 假设,集总、线性时不变元件构成的网络函数: F)=as”+ansl++as+a bns”+b-s"-1+…+bs+b。 =K(5-5a)(s-5:2)..(s-5m) (5-SpI)(S-5p2)...(s-5mn) F(s)是电路的网络函数,其稳定性要求: 极点在左半平面,jo轴上单极点。 但是,对于滤波器设计常用的转移函数,在右半S平 面无零点。 最小相位函数:在右半S平面无零点的转移函数,称为最小相位函数 稳定:极点x在左半平面,了⊙轴上单极点。 且右半平面无零点
( )( )...( ) ( )( )...( ) ... ... ( ) 1 2 1 2 1 0 1 1 1 0 1 1 p p pn z z zm n n n n m m m m s s s s s s s s s s s s K b s b s b s b a s a s a s a F s j F(s)是电路的网络函数,其稳定性要求: 极点在左半平面, 轴上单极点。 7-1、最小相位函数 j 最小相位函数:在右半S平面无零点的转移函数,称为最小相位函数 稳定:极点xx在左半平面, 轴上单极点。 且右半平面无零点。 j 假设,集总、线性时不变元件构成的网络函数: 但是,对于滤波器设计常用的转移函数,在右半S平 面无零点
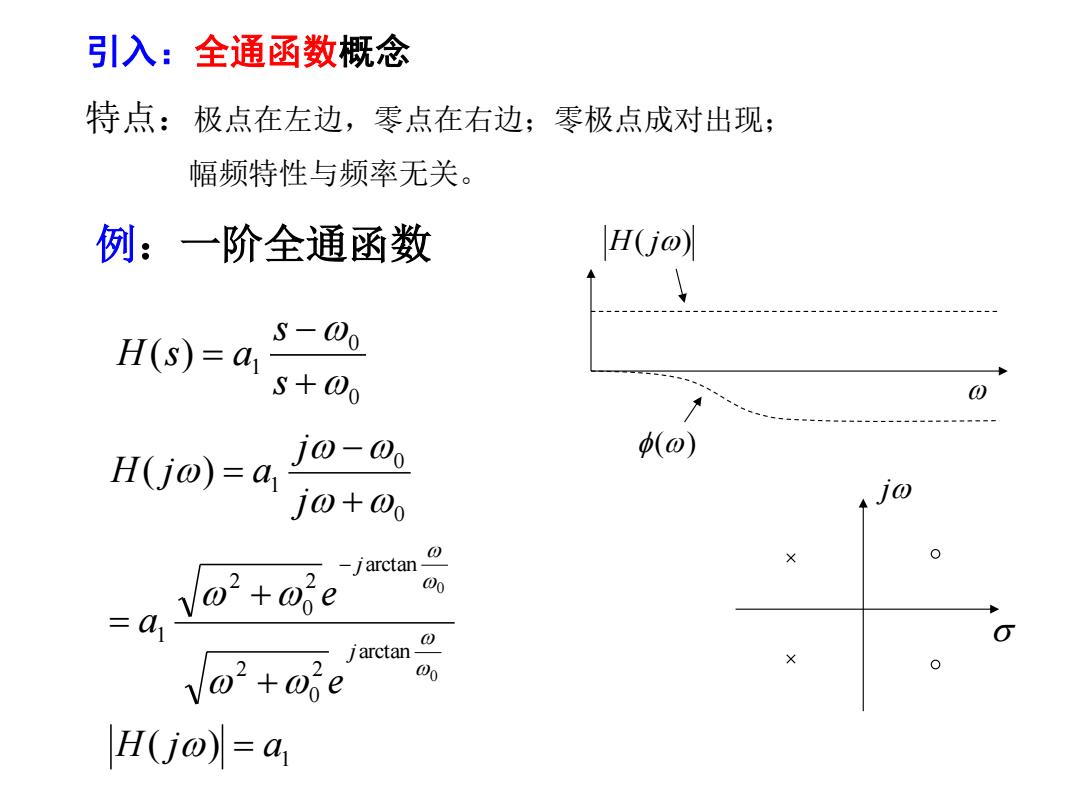
引入:全通函数概念 特点:极点在左边,零点在右边;零极点成对出现: 幅频特性与频率无关。 例:一阶全通函数 H(jo) H(s)=a s-00 S+00 H(j@)=a j0-0o (o) j0+00 0 -aYo'toie -j arctan 00 0 jarctan a"+aje 00 H(jo)=a
0 0 1 ( ) s s H s a 例:一阶全通函数 j 引入:全通函数概念 特点:极点在左边,零点在右边;零极点成对出现; 幅频特性与频率无关。 1 arctan 2 0 2 arctan 2 0 2 1 0 0 1 ( ) ( ) 0 0 H j a e e a j j H j a j j H( j) ()

结论:一个非最小相位函数可以表示为一个 最小相位函数与全通函数之乘积 例:非最小相位函数H1(S) H(s)=(s-S)(s-S)H(S) H,(o)=(s-,s-)H)s+s+) (s+5)(s+5) =(s+,+3)H)-s-) So (s+S)(s+5) A,(6)=5-s- 二阶全通 (s+S)(s+5) H2(s)=(s+S)s+5o)H(s)— H的镜像
( ) ( )( ) ( ) 1 0 0 H s s s s s H s 结论:一个非最小相位函数可以表示为一个 最小相位函数与全通函数之乘积 ( ) ( )( ) ( ) ( )( ) ( )( ) ( ) 2 0 0 0 0 0 0 0 H s s s s s H s s s s s s s s s H s 例:非最小相位函数H1 (s) j 0 s 0 s ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 0 0 0 0 0 0 0 0 0 0 1 0 0 s s s s s s s s s s s s H s s s s s s s s s H s s s s s H s 二阶全通 H1的镜像

结论:一个非最小相位函数可以表示为一个 最小相位函数与全通函数之乘积 H(s)= (S-S)S-5) 二阶全通 (S+S)(S+S) H2(S)=(s+S)(S+5)H(s) H1的镜像 So X X
( ) ( )( ) ( ) ( )( ) ( )( ) ( ) 2 0 0 0 0 0 0 0 H s s s s s H s s s s s s s s s H s j 0 s 0 s 二阶全通 H1的镜像 j 0 s 0 s j 0 s 0 s = 结论:一个非最小相位函数可以表示为一个 最小相位函数与全通函数之乘积