
A Famous Story ·在席·盖莫夫著的《从一到无穷大》中记载着一个关于古印度舍罕王 (Shirham)的故事: 舍罕王打算重赏“国际象棋”(真正的国际 象棋是后来进化演变来的)的发明人和进贡者, 宰相西萨.班·达伊尔(Sissa Ben Dahir)。这位 聪明的大臣的胃口看来并不大,他跪在国王面 前说:“陛下,请您在这张棋盘的第一个小格 内,赏给我一粒麦子;在第二个小格内两粒, 第三个给四粒,照这样下去,每个小格内都比 以前一个小格加一倍。陛下啊,把这样摆满棋 盘上所有64格的麦粒,都赏给您的仆人罢!” 舍罕王听后很生气,说:”你也太小看我 们印度国了,我拿一袋子麦子全给你好了。“ 西萨班·达伊尔坚持说还是按要求放满好。最后大家拿了许多袋麦子 过来都只完成了一小部分的填充工作,大家这才感觉到问题的严重。 6
6 A Famous Story 在席·盖莫夫著的《从一到无穷大》中记载着一个关于古印度舍罕王 (Shirham)的故事: 舍罕王打算重赏“国际象棋”(真正的国际 象棋是后来进化演变来的)的发明人和进贡者, 宰相西萨·班·达伊尔(Sissa Ben Dahir)。这位 聪明的大臣的胃口看来并不大,他跪在国王面 前说:“陛下,请您在这张棋盘的第一个小格 内,赏给我一粒麦子;在第二个小格内两粒, 第三个给四粒,照这样下去,每个小格内都比 以前一个小格加一倍。陛下啊,把这样摆满棋 盘上所有64格的麦粒,都赏给您的仆人罢!” 舍罕王听后很生气,说:”你也太小看我 们印度国了,我拿一袋子麦子全给你好了。“ 西萨·班·达伊尔坚持说还是按要求放满好。最后大家拿了许多袋麦子 过来都只完成了一小部分的填充工作,大家这才感觉到问题的严重
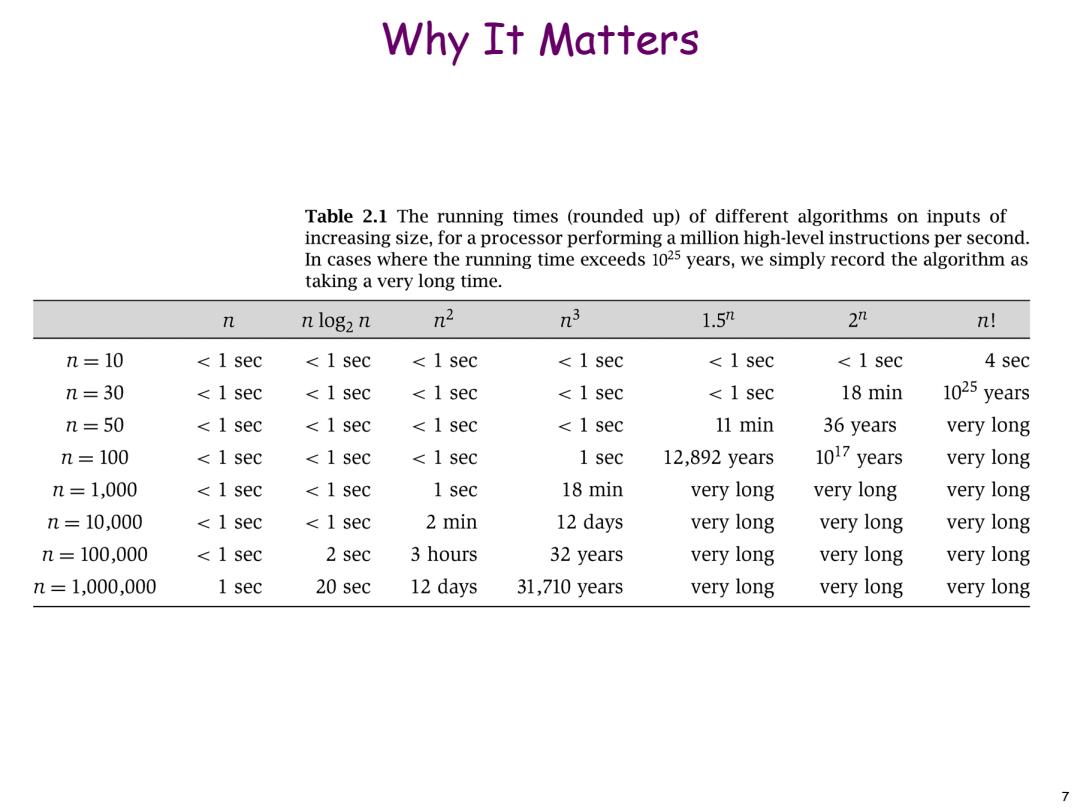
Why It Matters Table 2.1 The running times (rounded up)of different algorithms on inputs of increasing size,for a processor performing a million high-level instructions per second. In cases where the running time exceeds 1025 years,we simply record the algorithm as taking a very long time. n n log2 n n2 n3 1.5m 2n n! n=10 <1 sec <1 sec <1sec <1 sec <1 sec <1 sec 4 sec n=30 <1 sec <1 sec <1 sec <1 sec <1 sec 18 min 1025 years n=50 <1 sec <1 sec <1 sec <1 sec 11 min 36 years very long n=100 <1 sec <1 sec <1 sec 1sec 12,892 years 1017 years very long n=1,000 <1 sec <1 sec 1 sec 18 min very long very long very long n=10,000 <1 sec <1 sec 2 min 12 days very long very long very long n=100,000 <1 sec 2 sec 3 hours 32 years very long very long very long n=1,000,000 1 sec 20 sec 12 days 31,710 years very long very long very long 7
7 Why It Matters

What It Matters Shirham's story. The amount of wheat 0 1 2 3 0g00g 23 0884 63 20 21 22 23 年 223 4等 263 1 2 4 8 8388608 9223372036854775808 Sum 3 15 48gte 16777215 55g08: 18446744073709551615 It takes more than 2,000,000 years for a modern computer to count the wheat! Brute force solution to the max impendent set problem. If the graph has 100 vertices, Number of solution:2100= 1267650600228229401496703205376 8
8 What It Matters Shirham’s story. The amount of wheat 0 1 2 3 …… 23 …… 63 20 21 22 23 …… 223 …… 263 1 2 4 8 …… 8388608 …… 9223372036854775808 Sum 3 7 15 …… 16777215 …… 18446744073709551615 Brute force solution to the max impendent set problem. If the graph has 100 vertices, Number of solution: 2100= 1267650600228229401496703205376 It takes more than 2,000,000 years for a modern computer to count the wheat!

Polynomial and_exponential (多项式和指数) 上表中我们可以观察到n3和3n有巨大差别。 这个差别就是指数与多项式的差别。 在n3和3n中,如果n变成2n的话(也就是输入增大一 倍),两个数分别是以前的多少倍? 对于n3来说,是8倍,一个常数倍; 对于3n来说,是3n倍,这个倍数与n有关。 指数增长是恐怖的,在算法运行时间中应当尽量避免。很 多问题很容易就可以给出一个指数运行时间的穷举搜索算 法,但是否都存在多项式算法?(计算机科学的核心问题) 是否每个多项式时间的算法都有效?
9 Polynomial and exponential (多项式和指数) 上表中我们可以观察到 n 3 和 3 n 有巨大差别。 这个差别就是指数与多项式的差别。 在n 3 和 3 n 中,如果n变成2n的话(也就是输入增大一 倍),两个数分别是以前的多少倍? 对于 n 3 来说,是8倍,一个常数倍; 对于 3 n 来说,是3 n倍,这个倍数与n有关。 指数增长是恐怖的,在算法运行时间中应当尽量避免。很 多问题很容易就可以给出一个指数运行时间的穷举搜索算 法,但是否都存在多项式算法?(计算机科学的核心问题) 是否每个多项式时间的算法都有效?

数量级的差别 对于一个输入为n的问题,现给出两个算法A和B. 算法A运行100n步,算法B运行nlogn步。 哪个算法好? 若算法A运行n2+100n步,算法B运行2n2步。 哪个算法好? 很多时候我们认为n和n2之间的差异是较大的,而n和5n之 间的差异是微小的甚至可以忽悠不计的,怎样表达这种差 异? 用渐进表达式可以解决这个问题。 就算都是多项式,也需表现差异 0
10 数量级的差别 对于一个输入为n的问题,现给出两个算法A和B. 算法A运行100n步,算法B运行nlogn步。 哪个算法好? 就算都是多项式,也需表现差异 若算法A运行n 2+100n步,算法B运行2n2步。 哪个算法好? 很多时候我们认为n和n 2之间的差异是较大的,而n和5n之 间的差异是微小的甚至可以忽悠不计的,怎样表达这种差 异? 用渐进表达式可以解决这个问题