
省级精品课程—材料力学 4 例7-1图 解:首先求支座反力,由整个梁的平衡条件∑M,=0得,受,由∑M,=0 得X。名.利用∑y=0校核:克1+名1-g0+子=0,计算正确. 应用简化的截面法,得内力(考虑藏面的左边) 15 17 0版=2l-g1=32 M是1-子 0克l-g克l 考虑截面的右边也会到得同样的结果。具体考虑面的那一边应以计算简便为宜。 同以上计算过程可看到,简化的截面法的基础还是截面法,但在求内力时,“切”、“取” “代”等步骤以及分离体图都省略了,平衡方程也简化了,变成为直接由截面一边的外力求 出内力,因而简便易行。 §7.3剪力方程和弯矩方程剪力图和弯矩图 通常,梁的不同截面上的内力是不同的,也就是梁的内力随截面的位置而变化。设横截 面的位置用坐标x表示,则梁的横截面上的剪力和弯矩都可表示为坐标x的函数,即 Q=Q (x),M=M (X) 并分别称为尊力方得和弯矩方程 为了直观形象地 表示剪力和弯矩随酸面位变化的规律,将剪力方程和弯矩方程用曲线表 示:以截面位置x为横坐标,以剪力Q或弯矩M为纵坐标,绘出Q(x)或M(x)的图线 分别称为剪力图和弯矩图。 要提醒注意的是,为了便于今后的应用,多数情况下坐标轴的选择方法是:坐标原点放 梁的左端:x轴与染的轴线平行,并以指向右为正:Q轴以指向上为正:M轴以指向下为 正 例7-2作图示简支梁的剪力图和弯矩图 This document is generated by trial version of Print2Flash(www.print2flash.com) 109
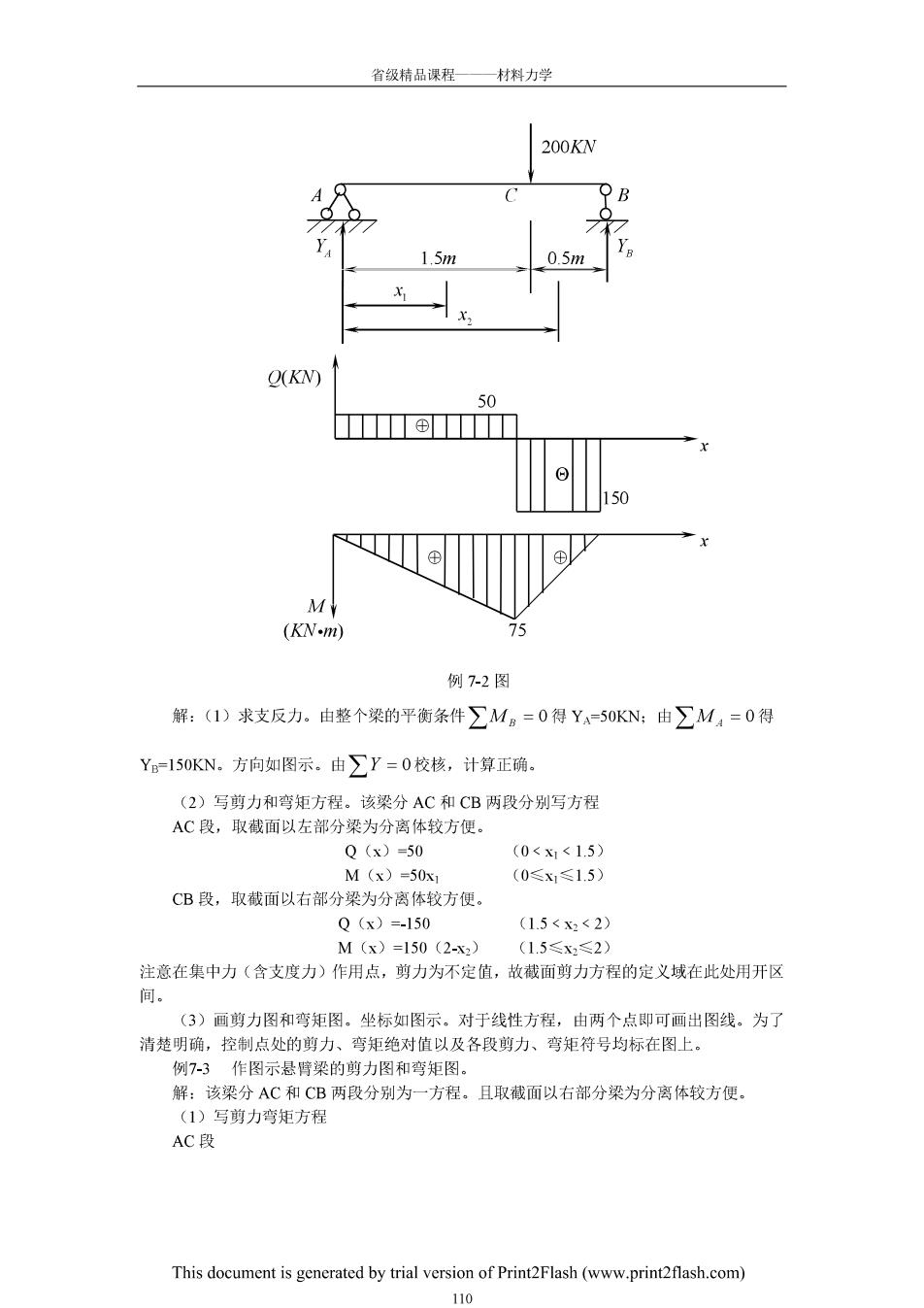
省领精品课程—一材料力学 200KW 15 Q(KN) 50 ⊕D 150 M (KN-m) 75 例7-2图 解:(1)求支反力。由整个梁的平衡条件∑Ma=0得YA-50KN:由∑M,=0得 Y=150KN.方向如图示。由∑Y=0校核,计算正确。 (2)写剪力和弯矩方程。该梁分AC和CB两段分别写方程 AC段,取截面以左部分梁为分离体较方便 Q(x)=50 (0<x<1.5) M(x)=50x (0≤x1≤1.5) CB段,取截面以右部分梁为分离体较方便。 Q(x)=-150 (1.5<x2<2) M(x)=150(2-x2) (15≤x≤2) 注意在集中力(含支度力)作用点,剪力为不定值,放截面剪力方程的定义域在此处用开区 (3)画剪力图和弯矩图。坐标如图示。对于线性方程,由两个点即可画出图线。为了 清楚明确,控制点处的剪力、弯矩绝对值以及各段剪力、弯矩符号均标在图上。 例7-3作图示悬臂梁的剪力图和弯矩图。 解:该梁分AC和CB两段分别为一方程。且取截面以右部分梁为分离体较方便。 写剪力弯矩方程 AC This document is generated by trial version of Print2Flash(www.printflash.com) 110
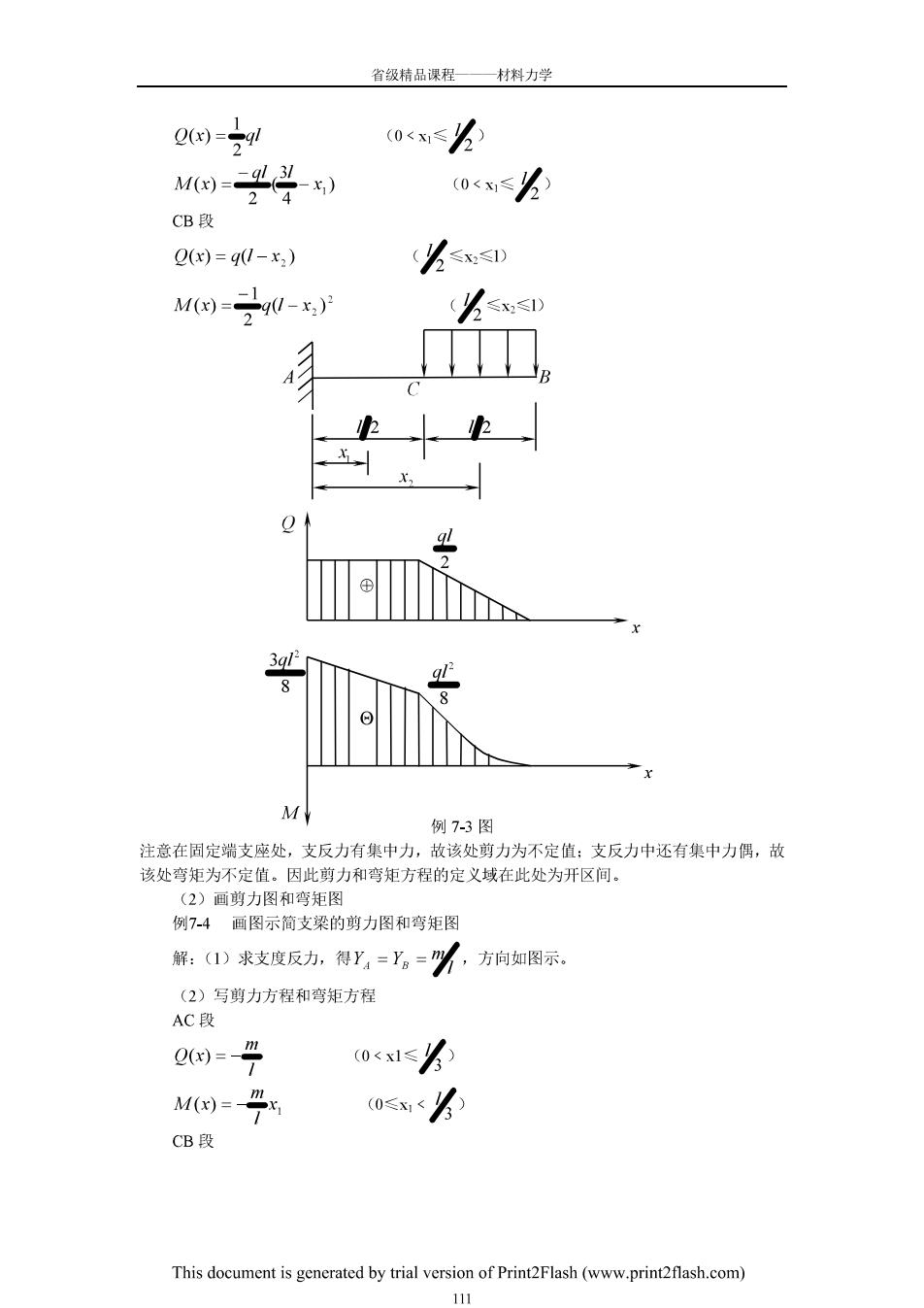
省级精品课程—材料力学 0- 0<x≤么 M兴) 0<x≤ CB Q(x)=90-x) (么≤D M)=90-) (么≤≤ M 例7-3图 注意在固定端支座处,支反力有集中力,故该处剪力为不定值:支反力中还有集中力偶,故 该处弯矩为不定值。因此剪力和弯矩方程的定义域在此处为开区间, (2)画剪力图和弯矩图 例74画图示简支梁的剪力图和弯矩图 解:(1)求支度反力,得Y4=Y。=%,方向如图示。 (2)写剪力方程和弯矩方程 AC段 0<1≤ 0≤w公 CB段 This document is generated by trial version of Print2Flash(www.print2flash.com) 111
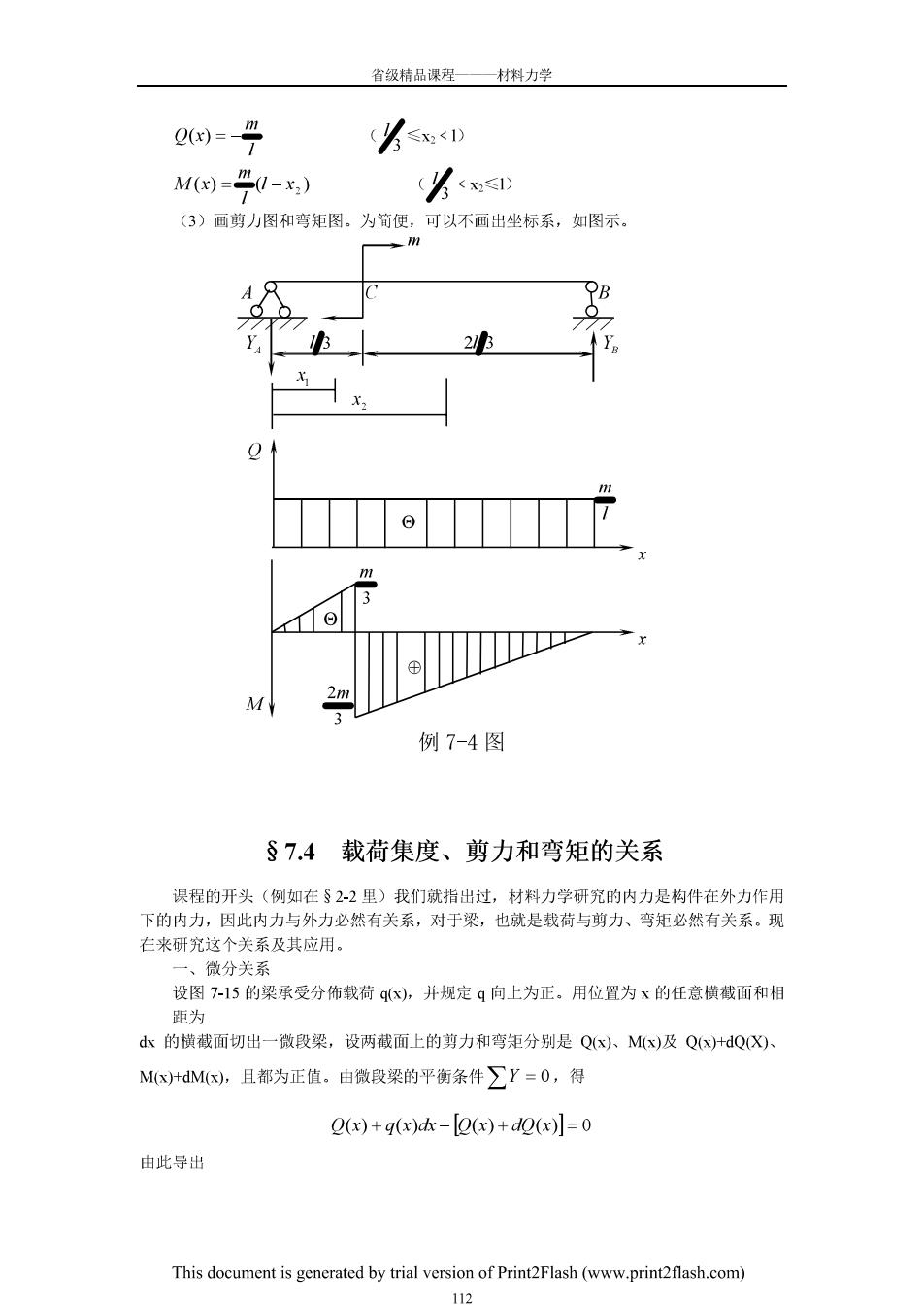
省领精品课程一材料力学 0)=只 (<D M=0-x,) (么<≤ (3)画剪力图和弯矩图。为简便,可以不画出坐标系,如图示。 X 例7-4图 §7.4载荷集度、剪力和弯矩的关系 课程的开头(例如在§2-2里)我们就指出过,材料力学研究的内力是构件在外力作用 下的内力,因此内力与外力必然有关系,对于梁,也就是载荷与剪力、弯矩必然有关系。现 在来研究这个关系及其应用。 ·、微分关系 设图7-15的梁承受分饰栽荷qx,并规定q向上为正。用位置为x的任意横截面和相 距为 dk的横截面切出一微段梁,设两截面上的剪力和弯矩分别是Q(x)、Mx)及Q(x)+QX、 Mx)+dMx,且都为正值.由微段梁的平衡条件∑Y=O,得 Q(x)+q(x)k-2(x)+d2(x]=0 由此导出 This document is generated by trial version of Print2Flash(www.printflash.com) 112
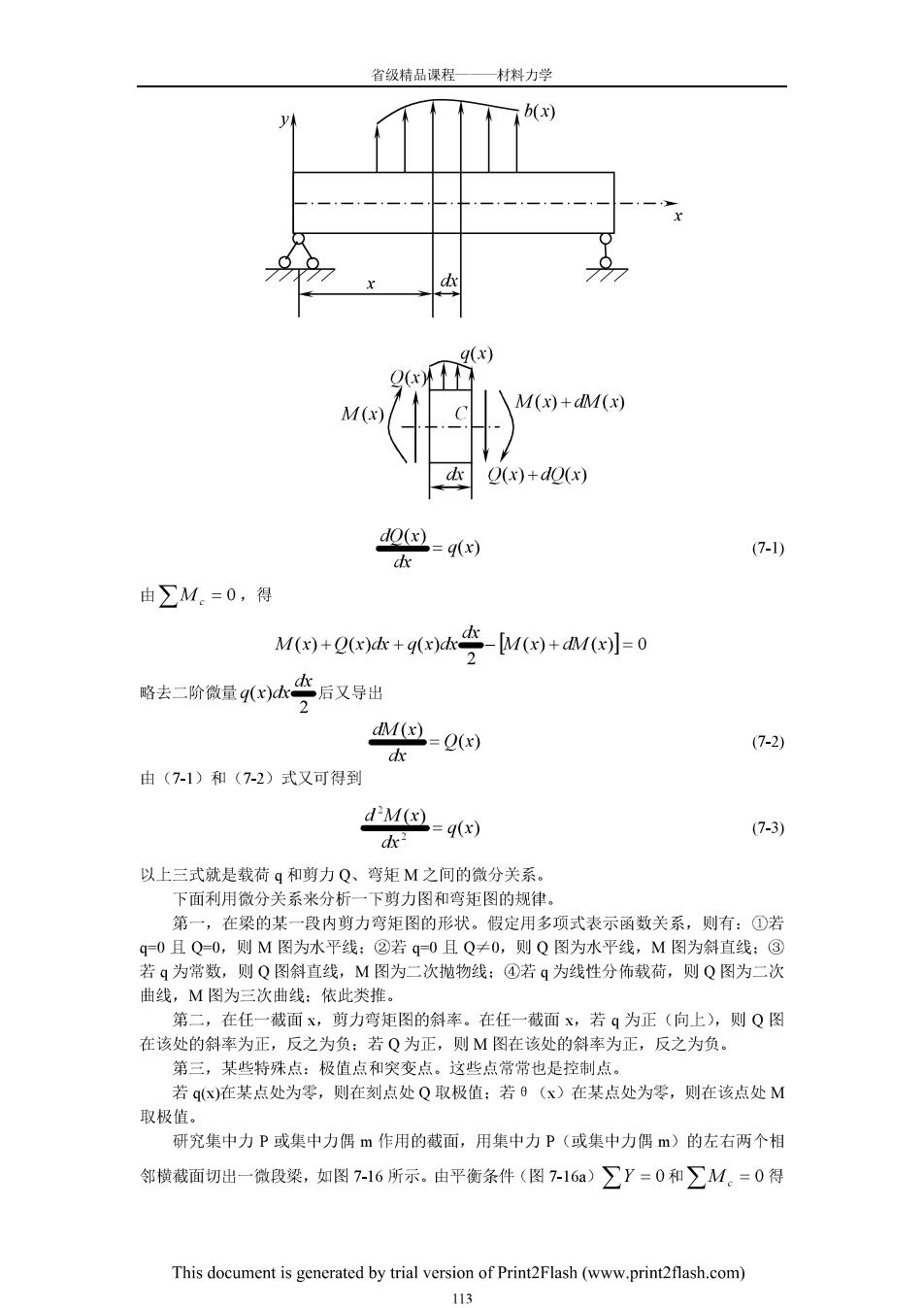
省领精品课程—材料力学 b(x) q(x) 2( M(x) \M()+dM(x) Q(x)+de(x) 7-1) 由∑M.=0,得 M+Qx达+qxh套M四+aM=0 略去二阶微量09k空后又导出 M(=0(x) (7-2) 由(7-1)和(7-2)式又可得到 dM因=4x) (7-3) ax- 以上三式就是载荷q和剪力Q、弯矩M之间的微分关系。 下面利用微分关系来分析一下剪力图和弯矩图的规律。 第一,在梁的某一段内剪力弯矩图的形状。假定用多项式表示函数关系,则有:①若 90且Q-0,则M图为水平线:②若q0且Q≠0,则Q图为水平线,M图为斜直线:@ 若q为常数,则Q图斜直线,M图为二次抛物线:④若q为线性分饰载荷,则Q图为二次 曲线,M图为三次曲线:依此类推。 第二,在任一截面x,剪力弯矩图的斜率。在任一裁面x,若q为正(向上),则Q图 在该处的斜率为正,反之为负:若Q为正,则M图在该处的斜率为正,反之为负。 第三,某些特殊点:极值点和突变点。这些点常常也是控制点。 若qx)在某点处为零,则在刻点处Q取极值:若0(x)在某点处为零,则在该点处M 取极 研究集中力P或集中力偶m作用的截面,用集中力P(或集中力偶m)的左右两个相 邻横截面切出一微段梁,如图7-16所示。由平衡条件(图-16a)∑Y=0和∑M。=0得 This document is generated by trial version of PrintFlash(www.printflash.com) 113