
Mini Tutorial:Convex set Euclidean balls and ellipsoids Convex Set (Euclidean)ball with center c and radius r: Example B(xc,r)={x|Ilx-xc2≤r}={xe+ru|lull2≤1} ellipsoid:set of the form {x|(x-xe)Tp-(x-x)≤1 with PS(i.e.,P symmetric positive definite) other representation:{e+Auu2 <1}with A square and nonsingular CLGO System Engineering by J.J.Gao 16
+ - System Engineering by J. J. Gao 16 Convex Set Example Mini Tutorial: Convex set
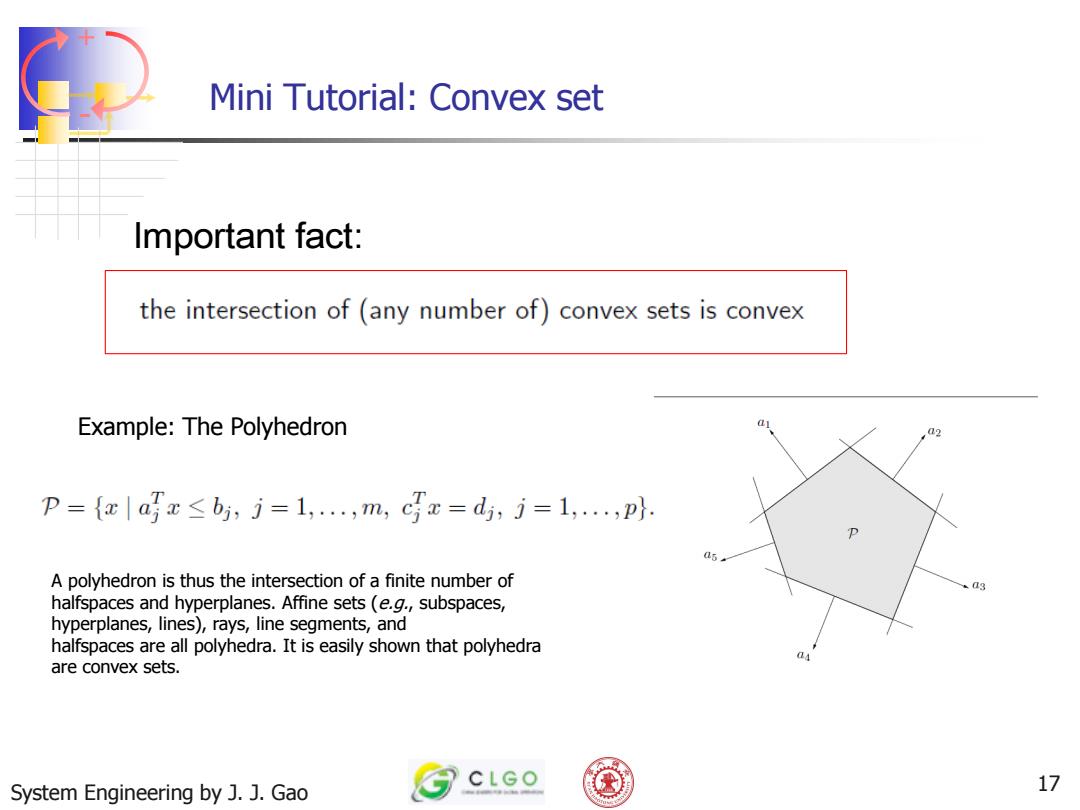
Mini Tutorial:Convex set Important fact: the intersection of(any number of)convex sets is convex Example:The Polyhedron P={x|a写x≤b,j=1,,m,cx=d,j=1,,p. A polyhedron is thus the intersection of a finite number of halfspaces and hyperplanes.Affine sets (e.g.,subspaces, hyperplanes,lines),rays,line segments,and halfspaces are all polyhedra.It is easily shown that polyhedra are convex sets. CLGO System Engineering by J.J.Gao 17
+ - System Engineering by J. J. Gao 17 Important fact: Example: The Polyhedron Mini Tutorial: Convex set A polyhedron is thus the intersection of a finite number of halfspaces and hyperplanes. Affine sets (e.g., subspaces, hyperplanes, lines), rays, line segments, and halfspaces are all polyhedra. It is easily shown that polyhedra are convex sets

Mini Tutorial:Convex function Definition f R"-R is convex if dom f is a convex set and f(0x+(1-9)y)≤0f(x)+(1-0)f(y) for all x,y∈domf,0≤9≤1 (v,f(y)) (x,f(x)) .f is concave if -f is convex CLGO System Engineering by J.J.Gao 18
+ - System Engineering by J. J. Gao 18 Mini Tutorial: Convex function

Mini Tutorial:Convex set and Convex function Examples on R convex: ·affine:a:x+bonR,for any a,b∈R ·exponential::eaz,for any a∈R ·powers:on R++,fora≥1ora≤0 ·powers of absolute value:|P on R,forp≥1 negative entropy:z logz on R++ concave: ·affine:a.x+bonR,for any a,b∈R ·powers:on R++,for0≤a≤1 logarithm:logx on R++ CLGO System Engineering by J.J.Gao 19
+ - System Engineering by J. J. Gao 19 Mini Tutorial: Convex set and Convex function

Mini Tutorial:Convex set and Convex function Examples on R"and Rmxn affine functions are convex and concave;all norms are convex examples on R" .affine function f(x)=aT+b ·norms::zllp=(∑-1lclP)1/P for p≥1;lzlloo=maxk examples on Rmxn(m x n matrices) 。affine function m n fX))=tr(ATX)+b=∑∑A与X+b i=1j=1 spectral (maximum singular value)norm f(X)=lXll2 amax(X)=(Amax(XTX))1/2 CLGO System Engineering by J.J.Gao 20
+ - System Engineering by J. J. Gao 20 Mini Tutorial: Convex set and Convex function