
Input-Output Multipath Channel Functions The presence of multipath can be formally described by the some proper "1/O Channel Functions"that can be associated with the radio channel hpl-discrete channel:N,rays/paths hp2-static channel:channel properties don't vary in time>terminals don't move (in practice,fluctuations in time can be neglected during transmission) x() y(t)? H(f),h(t) u(t) H();h() v(t)? The I/O channel functions establish a correspondence between the input and the output signals,i.e.formulates the effects of the environment on the propagating signal
Input-Output Multipath Channel Functions The presence of multipath can be formally described by the some proper “I/O Channel Functions” that can be associated with the radio channel hp1 - discrete channel: Nr rays/paths hp2- static channel: channel properties don’t vary in time terminals don’t move (in practice, fluctuations in time can be neglected during transmission) H(f), h(t) H+(f) ; h0(t) y(t) ?? The I/O channel functions establish a correspondence between the input and the output signals, i.e. formulates the effects of the environment on the propagating signal v(t) ?? x(t) u(t)

Channel Lowpass Impulse Response(1/2) According to hp 1-2,the i-th path(i=1,..,N.)introduces: amplitude loss (p)due to the attenuation produced by propagation and by the interactions between the wave and the environment along the path; time shift(t)due to propagation delay; phase shift(0)due to the phase change along the path; y)=pAt-t)cos2m,6≥t+6t)p+e,) y()()=icp 0=2A-小b-i).2 u(-t) V()
Channel Lowpass Impulse Response (1/2) According to hp 1-2, the i-th path (i=1,.., Nr ) introduces: amplitude loss (ρi ) due to the attenuation produced by propagation and by the interactions between the wave and the environment along the path; time shift (ti ) due to propagation delay; phase shift (θi ) due to the phase change along the path; y(t) = yi(t) = ℜ i=1 Nr ∑ e ρi ⋅ A t − t ( i)⋅ ej 2π f0t ⋅ e− j 2π f0ti ⋅ ejα t−t ( i) ⋅ e− jφ0 ejθi i=1 Nr ∑ ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ ( ) ( ) ( ( ) ( ) ) i i i 0 i i 0 i y t = ρ ⋅A t − t ⋅cos 2πf t − t + α t − t − ϕ + θ y(t) = ℜe ρi ⋅ A t − t ( i)⋅ ejα t−t ( i) ⋅ e− jφ0 ⋅ e− j 2π f0ti ⋅ ejθi ⋅ ej 2π f0t i=1 Nr ∑ ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ u(t-ti ) v(t)

Channel Lowpass Impulse Response(2/2) v(t)represents the complex envelope of the received signal: v()-p.-u6-t)ct) i=l .u(t-t)=tutd(well known property of the 8-distribution) ↓ 60-2了能-f-gea--j2,c-ta0u6- k0=2p6t-4)4w网 Channel lowpass impulse response h个 v()-.G)w6-5)-Jb(-)uG)-h.()out)
Channel Lowpass Impulse Response (2/2) ( ) ( ) ( ) ∑ = θ − π ⋅ = ρ ⋅ − ⋅ r i 0 i N i 1 j 2 f t i i v t u t t e (well known property of the ( ) ( ) ( ) δ-distribution) ∫ ∞ −∞ u t − t = δ ξ − t ⋅u t − ξ dξ i i ( ) ( ) ( ) ( ) ( ) ( ) ( ) ∑ ∫ ∫ ∑ ∞ −∞ = θ − π ⋅ = θ − π ⋅ ∞ −∞ v t = ρ δ ξ − t ⋅u t − ξ dξ⋅e = ρ δ ξ − t e u t − ξ dξ r i 0 i r i 0 i N i 1 j 2 f t i i N i 1 j 2 f t i i v(t) represents the complex envelope of the received signal: h0 (t) ≡ ρi δ t − t ( i)ej θi−2π f0⋅t ( i) i=1 Nr ∑ v(t) h ( ) u(t )d h (t ) u( )d h (t) u(t) = ∫ 0 ξ ⋅ − ξ ξ = ∫ 0 − ξ ⋅ ξ ξ = 0 ⊗ ∞ −∞ ∞ −∞ |h0| t ti ρi Channel lowpass impulse response
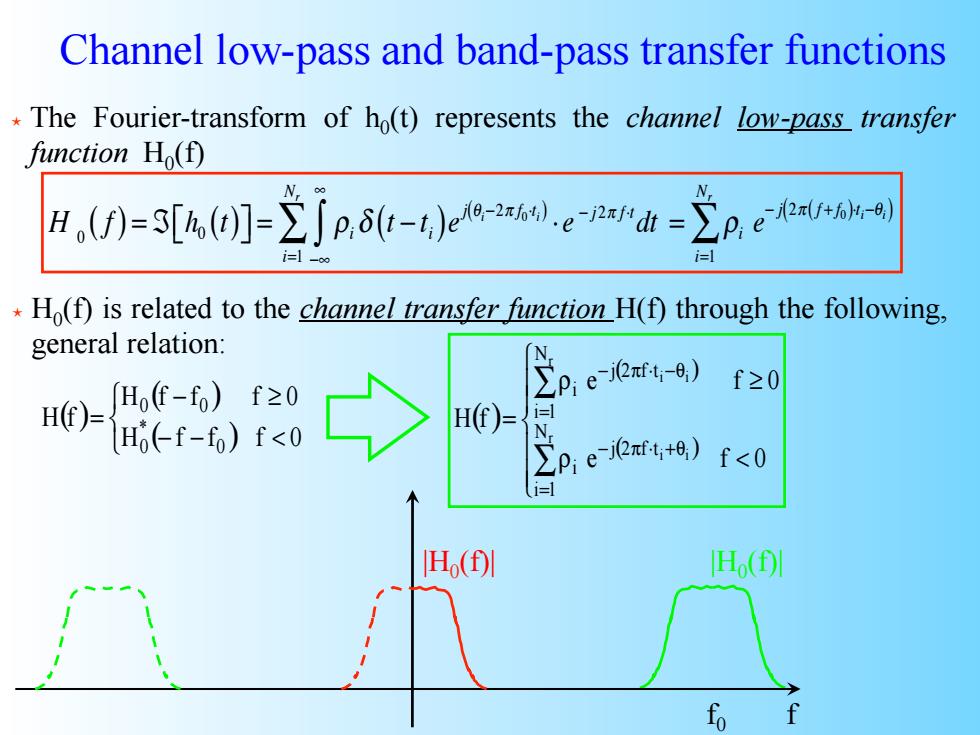
Channel low-pass and band-pass transfer functions The Fourier-transform of ho(t)represents the channel low-pass transfer function Ho(f) H)-3[(Jp.-t)p Ho(f)is related to the channel transfer function H(f)through the following, general relation: 66切e0 f20 Ho(-f-fo)f<0 H(f)= 1=] N Pejeπttt8)f<0 H()I 旧( fo
Channel low-pass and band-pass transfer functions The Fourier-transform of h0(t) represents the channel low-pass transfer function H0(f) H 0 ( f ) = ℑ h0 ⎡ (t) ⎣ ⎤⎦ = ρi δ t − t ( i)ej θi−2π f0⋅t ( i) ⋅ e − j 2π f ⋅t dt −∞ ∞ ∫ i=1 Nr ∑ = ρi e − j 2π f + f ( 0 )⋅ti−θ ( i) i=1 Nr ∑ H0(f) is related to the channel transfer function H(f) through the following, general relation: ( ) ( ) ( ) ⎩ ⎨ ⎧ − − < − ≥ = H f f f 0 H f f f 0 H f 0 * 0 0 0 f |H0(f)| |H0(f)| f0 ( ) ( ) ( ) ⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ ρ < ρ ≥ = ∑ ∑ = − π ⋅ +θ = − π ⋅ −θ e f 0 e f 0 H f r i i r i i N i 1 j 2 f t i N i 1 j 2 f t i