§4.1傅立叶级数和变换简史 fx) 傅立叶级数 任何周期(周期为2)函数均可表示成不同频率的正弦和 T=2π 余弦函数的加权和: 00 2sinx ao nπx nπX f(x)= ancos +bnsin) n=1 3cosx an=f()cosdx (n=0.12. + 4sin2x + ba=f)sn2dkn=1.23) cos3x
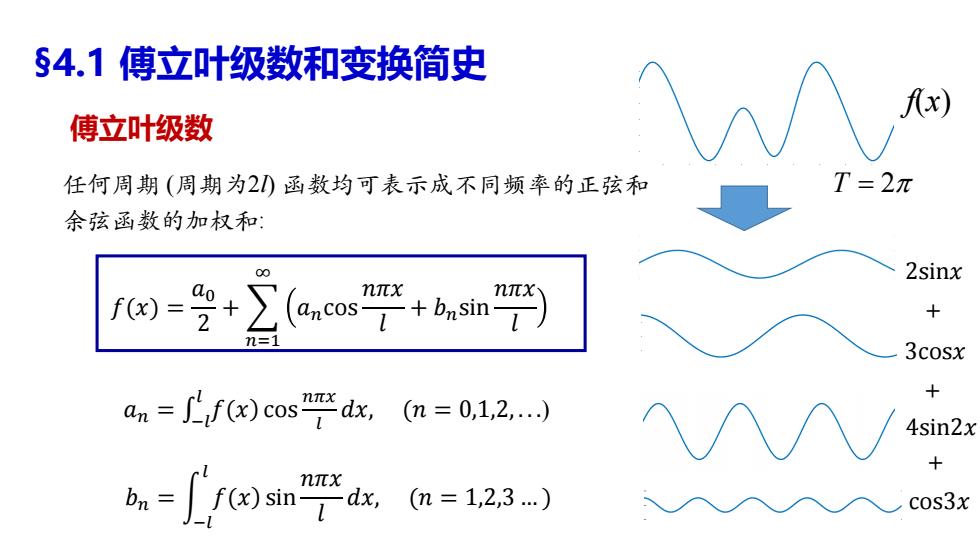
傅立叶级数 任何周期 (周期为2l) 函数均可表示成不同频率的正弦和 余弦函数的加权和: f(x) 𝑓(𝑥) = 𝑎0 2 + 𝑛=1 ∞ 𝑎𝑛cos 𝑛𝜋𝑥 𝑙 + 𝑏𝑛sin 𝑛𝜋𝑥 𝑙 ��− = �𝑎� 𝑙 𝑓(𝑥) cos 𝑛𝜋𝑥 𝑙 𝑑𝑥, (𝑛 = 0,1,2, . . .) 𝑏𝑛 = න −𝑙 𝑙 𝑓(𝑥) sin 𝑛𝜋𝑥 𝑙 𝑑𝑥, (𝑛 = 1,2,3 … ) 2sin𝑥 3cos𝑥 4sin2𝑥 cos3𝑥 + + + T 2 §4.1 傅立叶级数和变换简史

§4.1傅立叶级数和变换简史 傅立叶级数 一种直观解释:光的色散现象 红 橙 白色 黄十 绿 蓝靛紫 白色 =∑an Sin(nx)
一种直观解释:光的色散现象 §4.1 傅立叶级数和变换简史 傅立叶级数