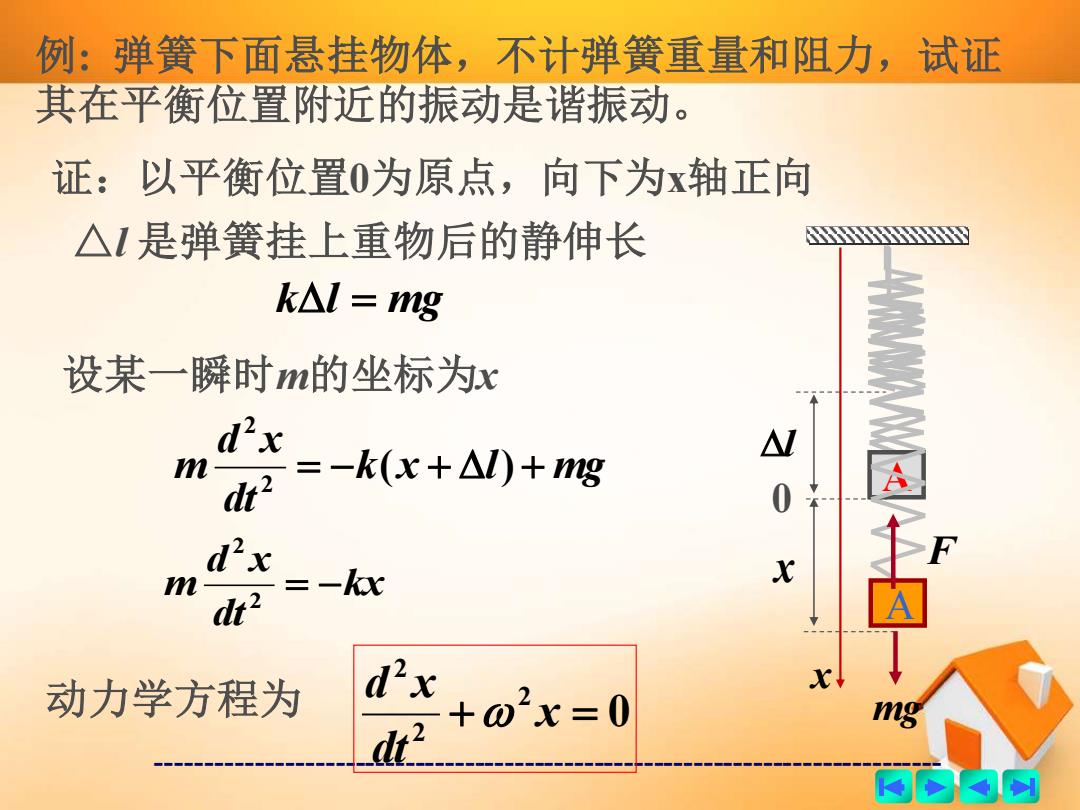
例:弹簧下面悬挂物体,不计弹簧重量和阻力,试证 其在平衡位置附近的振动是谐振动。 证:以平衡位置0为原点,向下为x轴正向 △1是弹簧挂上重物后的静伸长 k△l=mg 设某一瞬时m的坐标为x dx dt2 =-k(x+△l)+g 0 d2x =-c 动力学方程为 d'x dr2 +o2x=0 mg 商的内网
------------------------------------------------------------------------------- 例: 弹簧下面悬挂物体,不计弹簧重量和阻力,试证 其在平衡位置附近的振动是谐振动。 A 证:以平衡位置0为原点,向下为x轴正向 x 0 l △l 是弹簧挂上重物后的静伸长 kl = mg 设某一瞬时m的坐标为x A x F mg k x l mg dt d x m = − ( + ) + 2 2 kx dt d x m = − 2 2 动力学方程为 0 2 2 2 + x = dt d x

§10.2简谐振动的运动学 一、简谐振动的运动学方程 微分方程 d'x +02x=0 运动学方程 x=Acos(@t+p) A、由初始条件所决定 x 1.速度 =-A@sin(@t+o) dt D=±0NA2-x2 2.加速度 Q=- =-Ao'cos(@t+o) dt 两的肉的
------------------------------------------------------------------------------- §10.2 简谐振动的运动学 一、简谐振动的运动学方程 0 2 2 2 + x = dt d x 微分方程 运动学方程 cos( ) = +0 x A t A、0 由初始条件所决定 1.速度 sin( ) = = − +0 A t dt dx 2 2 = A − x 2.加速度 cos( ) 0 2 = = −A t + dt d a a x 2 = −

二.描述谐振动的三个特征量 1.振幅A 由初始条件决定 xo=AcosPo t=0 合-1sap, 4= 2.周期T 完成一次完全振动所需的时间 x=Acos(at+o)=Acosl@(t+T)+oo] =Ac0s(ot+p+2π) 两的肉例
------------------------------------------------------------------------------- 二. 描述谐振动的三个特征量 1.振幅A 由初始条件决定 t=0 = − = 0 0 0 0 sin cos A x A 2 2 0 2 0 A = x + 2. 周期T 完成一次完全振动所需的时间 cos( ) = +0 x A t 0 = Acos (t +T)+ cos( 2 ) = A t +0 +

周期T: T 2π ) 1 频率 V= T 2元 圆频率:0=2rV 固有圆频率:仅由振动系统的力学性质所决定频率 固有圆频率 固有振动周期 k 2 弹簧振子 0= m T=2πk 单摆 0= T=2r】 g mgh 复摆 0=V T= mgh 两的肉的
------------------------------------------------------------------------------- 周期T: 2 T = 频率: 2 1 = = T 圆频率: = 2 固有圆频率:仅由振动系统的力学性质所决定频率 弹簧振子 固有圆频率 m k = 固有振动周期 k m T = 2 单摆 l g = g l T = 2 复摆 I mgh = mgh I T = 2