
§5-2 Equation of diffusion current A basis of polarographically quantitative analysis On dropping mercury electrode: Mn+ + ne- +Hg M(Hg) Ede = Eo + ln RT nF Ce Ca Where Ce is Mn+ concentration on the electrode surface, Ca is M concentration in amalgam on electrode surface
§5-2 Equation of diffusion current A basis of polarographically quantitative analysis On dropping mercury electrode: Mn+ + ne- +Hg M(Hg) Ede = Eo + ln RT nF Ce Ca Where Ce is Mn+ concentration on the electrode surface, Ca is M concentration in amalgam on electrode surface

Diffusion layer Bulk solution Electrode Diffusion layer Bulk solution Electrode d Concentration polarization around mercury drop
Diffusion layer Bulk solution Electrode Diffusion layer Bulk solution Electrode d Concentration polarization around mercury drop

When the applied voltage exceeds the decomposition voltage, diffusion-controlled current is expressed as: i = K(C-Ce ) When the applied voltage gets more negative, Ce →0, then id = KC Id reaches a limiting value proportional to ion concentration C in bulk solution, and do not changes with applied voltage longer
When the applied voltage exceeds the decomposition voltage, diffusion-controlled current is expressed as: i = K(C-Ce ) When the applied voltage gets more negative, Ce →0, then id = KC Id reaches a limiting value proportional to ion concentration C in bulk solution, and do not changes with applied voltage longer

In above equations, K is called Ilkovic constant, it is expressed as follows: Ilkovic equation-diffusion current equation K = 607 n D1/2m2/3t 1/6 id = 607nD1/2m2/3t 1/6C Average limiting diffusion current denoting average current on mercury drop from drop forming to falling (mA) Number of transferring electrons in electrode reaction(e/mol) Diffusion coefficient of electroactive analyte in solution(cm2 .sec-1 ) Mercury mass flow rate(mg.sec-1 ) Drop time (sec) Concentration of electro-active analyte(mmol.L-1 ) From above equation, we can find that when temperature, matrix solution and capillary characteristic are kept constant, id is proportional to C
In above equations, K is called Ilkovic constant, it is expressed as follows: Ilkovic equation-diffusion current equation K = 607 n D1/2m2/3t 1/6 id = 607nD1/2m2/3t 1/6C Average limiting diffusion current denoting average current on mercury drop from drop forming to falling (mA) Number of transferring electrons in electrode reaction(e/mol) Diffusion coefficient of electroactive analyte in solution(cm2 .sec-1 ) Mercury mass flow rate(mg.sec-1 ) Drop time (sec) Concentration of electro-active analyte(mmol.L-1 ) From above equation, we can find that when temperature, matrix solution and capillary characteristic are kept constant, id is proportional to C
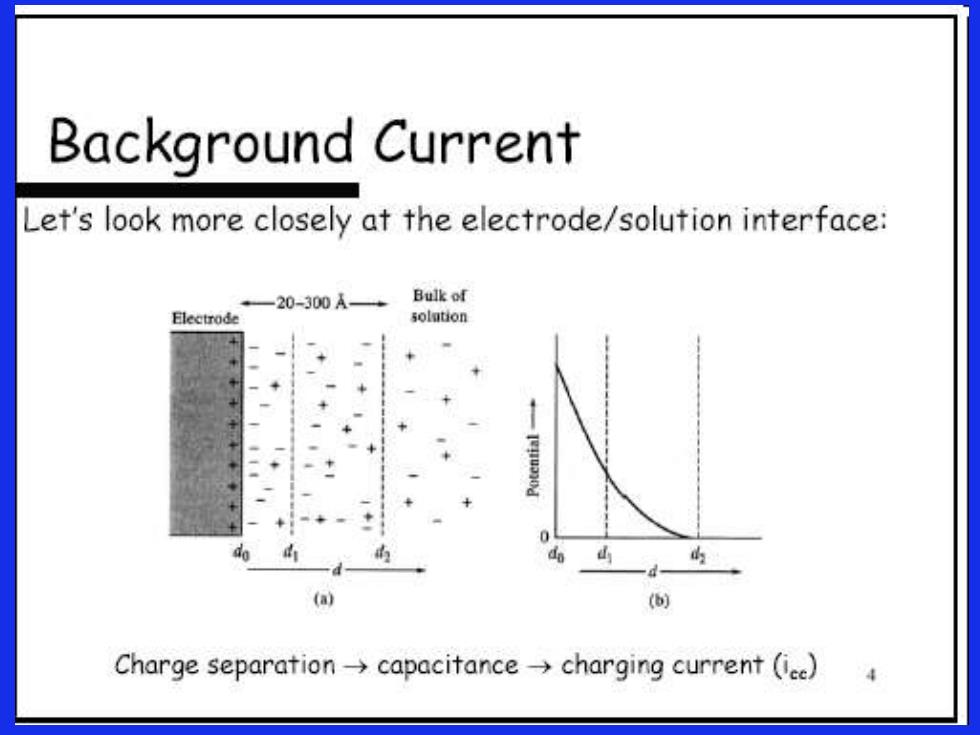
Background Current Let's look more closely at the electrode/solution interface: +—20-300A—→ Bulk of Electrode solution (a) ( Charge separation->capacitance->charging current (ice)