0数制的转换计建机科学与技术学院十进制数转换成二进制数转换方法是,整数部分“除以2取余数,反序排列”:小数部分“乘2取整数,正序排列”例托洋妞象囍进建精数8m159例°把2制数459转换成十本进制数849余3余12945余226118114OF317285(由=(237条1hB余120(59)10=(111011)2(459)10=(1CB)16112025/4/6
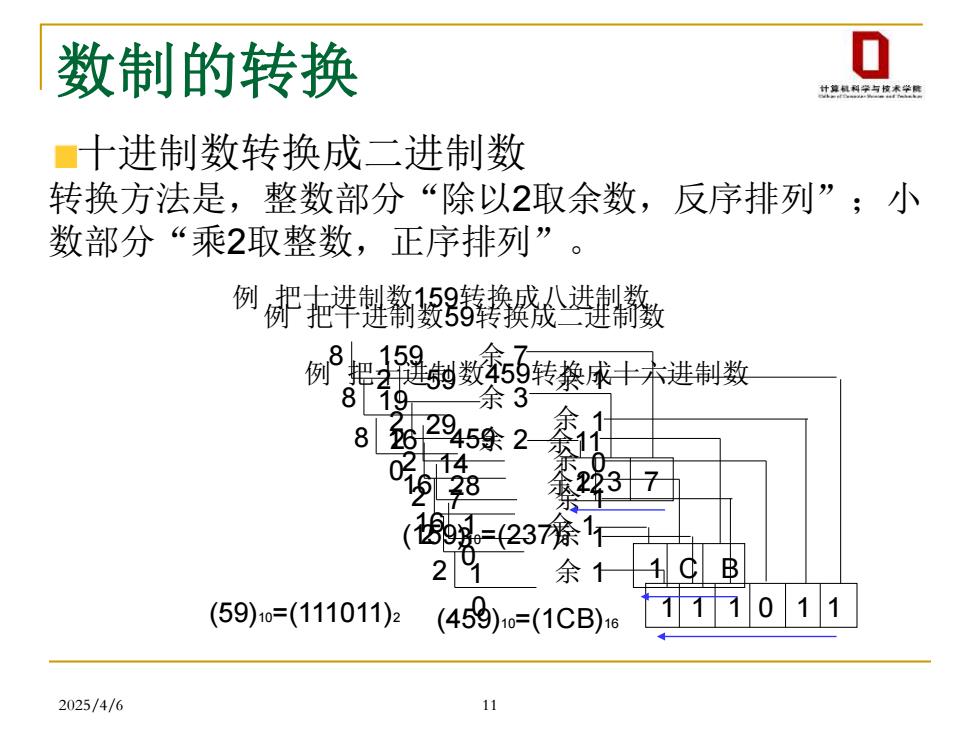
2025/4/6 11 十进制数转换成二进制数 转换方法是,整数部分“除以2取余数,反序排列”;小 数部分“乘2取整数,正序排列”。 例 把十进制数59转换成二进制数 2 59 2 29 2 14 2 7 2 3 2 1 (59)10=(111011)2 0 1 1 0 1 1 1 1 1 1 0 1 1 余 余 余 余 余 余 例 把十进制数159转换成八进制数 8 159 8 19 8 2 0 (159)10=(237)8 2 3 7 余 7 余 3 余 2 例 把十进制数459转换成十六进制数 16 459 16 28 16 1 0 (459)10=(1CB)16 1 C B 余11 余12 余 1 数制的转换

0数制的转换计算机科学与技术学院例如:将十进制小数0.625转换成二进制数用乘2取整法,转换过程如下:取出整数1 (最高位)0.625X2=1.25取出整数 0↓0.25X2=0.5取出整数1 (最低位)0.5X2=1.0即0.625=0.101B注意:有的十进制小数不能用二进制小数精确地表示出来
数制的转换 例如:将十进制小数0.625转换成二进制数 用乘2取整法,转换过程如下: 0.625×2=1.25 取出整数 1 (最高位) 0.25×2=0.5 取出整数 0 ↓ 0.5×2=1.0 取出整数 1 (最低位) 即0.625 =0.101B 注意:有的十进制小数不能用二进制小数精确地表示出 来

0数制的转换计算L学与技术学阶二进制、八进制、十六进制数转换为十进数对于任意一个二进制数、八进制数、十六进制,可以写出它的按权展开式,再相加求和即可例如:(1111.11)2= 1 X23+1X 22+1×21+1X20 +1 ×2-1+1X 2-2=15.75(A10B.8)16=10 X 163+1 X 162+0 X 161+11X 160+8X 16-1= 41227.5
数制的转换 ◼ 二进制、八进制、十六进制数转换为十进数 对于任意一个二进制数、八进制数、十六进制,可以 写出它的按权展开式,再相加求和即可 例如: (1111.11)2= 1×2 3+1×2 2+1×2 1+1×2 0 +1×2 -1 +1×2 -2=15.75 (A10B.8)16=10×163+1×162+0×161+11×160 +8×16-1= 41227.5

0数制的转换计算机科学与技术学院二进制数与八进制数的相互转换二进制数转换成八进制数的方法是“三位合一位”法。例如将11111101.101转换成八进制数:011111101:101??1375.5转换结果为11111101.101B=375.5Q。八进制数转换成二进制数方法,正好与二进制数转换成八制数的方法相逆,即“一位扩展三位”法
数制的转换 ◼ 二进制数与八进制数的相互转换 二进制数转换成八进制数的方法是“三位合一位”法。 例如 将11111101.101转换成八进制数: 011 111 101 . 101 ↓ ↓ ↓ ↓ 3 7 5 . 5 转换结果为11111101.101B = 375.5Q。 八进制数转换成二进制数方法,正好与二进制数转换 成八制数的方法相逆,即“一位扩展三位”法

0计算棋科学与技术学院例如将246.45Q转换成二进制数2546.4++++010 100 110. 100 101转换结果为246.45Q=010100110.100101 B
◼ 例如 将246.45Q转换成二进制数 2 4 6 . 4 5 ↓ ↓ ↓ ↓ ↓ 010 100 110 . 100 101 ◼ 转换结果为246.45Q = 010100110 .100 101 B