P为观察点,S是包围点的一个任意封 闭曲面。基尔霍夫选择格林函数G为由 P点向外发散的单位振幅的球面波。在 S S面上任意一点P处,G的取值为 G(B)= exp(jkro1) 1o1 式中,ro1表示从P指向P的矢量ro1的长度。 ds =0
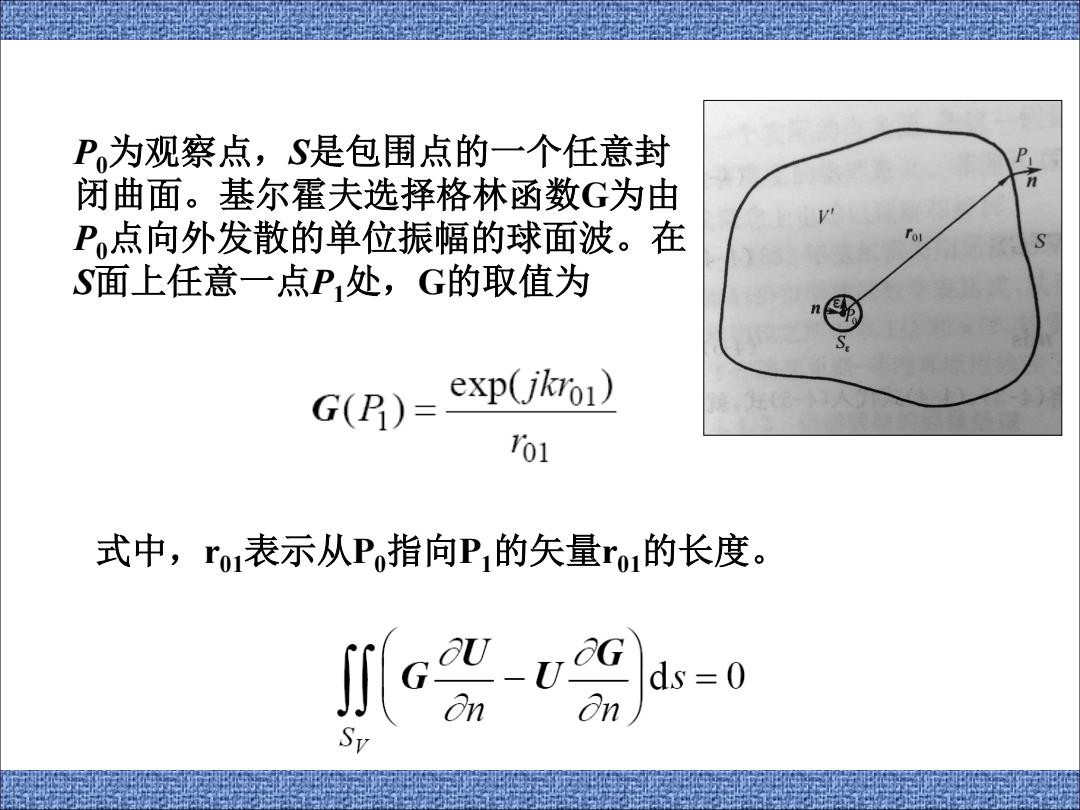
P0为观察点,S是包围点的一个任意封 闭曲面。基尔霍夫选择格林函数G为由 P0点向外发散的单位振幅的球面波。在 S面上任意一点P1处,G的取值为 式中,r01表示从P0指向P1的矢量r01的长度

由于格林函数在P点是无界的和不连续 的,因此P点是一个奇异点,而格林定 P 理要求公式中的函数G和U及其一阶、 二阶偏导数及方向导数aG/an、U/on在 S 被S所包围的体积中必须是单值连续的, 所以点必须从积分区中去掉,为了解决 这一矛盾,用一个以P为球心,半径为 的小球面嵌在P点周围。 Sy=S+Se S面上的外法线方向是由S面上的点指向外侧,而S面上 的外法线方向是空腔内S,上的点指向P点,即沿半径指向 球心P。。曲面S和S之间包围的体积为V',在V'内函数G、 U连续有界,G、U的一阶、二阶偏导数及方向导数单值 连续
由于格林函数在P0点是无界的和不连续 的,因此P0点是一个奇异点,而格林定 理要求公式中的函数G和U 及其一阶、 二阶偏导数及方向导数∂G/∂n、∂U/∂n在 被S所包围的体积中必须是单值连续的, 所以点必须从积分区中去掉,为了解决 这一矛盾,用一个以P0为球心,半径为 ε的小球面嵌在P0点周围。 S面上的外法线方向是由S面上的点指向外侧,而Sε面上 的外法线方向是空腔内Sε上的点指向P0点,即沿半径指向 球心P0 。曲面S和Sε之间包围的体积为V ′,在V ′内函数G、 U连续有界,G、U的一阶、二阶偏导数及方向导数单值 连续

G- ds =0 a- ds 在S面上,n与r的方向相反,cos(n,ro1)=-1,因而 aan=-a/ar,又因为=e,所以对于S上的P1点有 G(R)= 及 。 E n ds
在Sε面上,n与r的方向相反,cos(n, r01) =-1,因而 ∂/∂n=- ∂/∂r ,又因为r=ε,所以对于Sε上的P1点有

g兰 gg对儿e lim 6→0 -ogt ds G(B)= 01

基尔霍夫积分定理 ds 因这一定理在声学上亥姆霍兹也曾导出过,所以有的文献 中称之为亥姆霍兹—基尔霍夫积分定理。利用这一定理就 可以把单色光波场中任一点P的场的复振幅用包围P的任 意封闭曲面上各点的光的复振幅U及U/on表示出来,因 此,这本身就是由边界条件求解场的复振幅分布问题。计 算中所用的格林函数G就是为了解决问题而引入的一个辅 助函数
因这一定理在声学上亥姆霍兹也曾导出过,所以有的文献 中称之为亥姆霍兹—基尔霍夫积分定理。利用这一定理就 可以把单色光波场中任一点P0的场的复振幅用包围P0的任 意封闭曲面上各点的光的复振幅U及∂U/∂n表示出来,因 此,这本身就是由边界条件求解场的复振幅分布问题。计 算中所用的格林函数G就是为了解决问题而引入的一个辅 助函数。 基尔霍夫积分定理