电子科技大学：《光学原理 Principles of Optics》课程教学资源（课件讲稿）第四章 标量衍射理论基础

41 惠更斯-菲涅耳原理

4-1

波阵面上任一点均可视为能向外发射子波的子波源波面 前方空间某一点P的振动就是到达该点的所有子波的相千叠加： S

S D D S P z  '  z Q  r 惠菲原理1

光源S 四个假设： ①波面是一等相面。→光源S上所有面元ds具有相同位相（令其为0) ②次波源ds在P点的振幅与"成反比。→次波是球面波 ③次波源ds在P点的振幅正比于其面积且与倾角日有关，随θ的增大而减小。 ④次波源ds在P点的位相由光程△=nr决定，→p= 2π 入

p r  N   光源S dS 0 r Q 四个假设： ①波面是一等相面。→光源S上所有面元ds具有相同位相（令其为0） ②次波源ds 在P点的振幅与 r 成反比。→ 次波是球面波 ③次波源ds 在P点的振幅正比于其面积且与倾角θ有关，随 θ的增大而减小。 ④次波源ds 在P点的位相由光程Δ=nr 决定， →      2

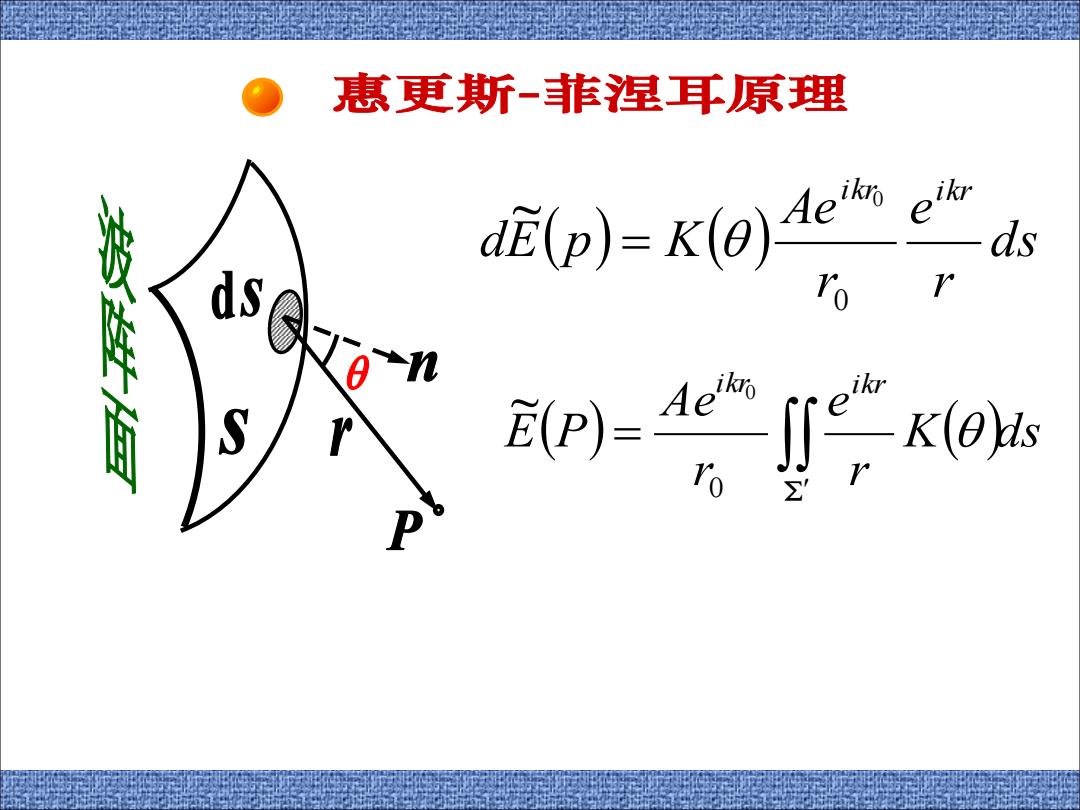
惠更斯-菲涅耳原理 a间p)=Ko)4 ikro ikr e ds 玻面 ds 1r0 S 网广o

    ds r e r Ae dE p K ikr ikr 0 0   ~   K ds r e r Ae E P ikr ikr    Σ  0 0 ~

E(P)K(oys K(©)为倾斜因子，描写子波振幅随方向变化，是2点 面元的法线与2P方向的夹角（也称衍射角）。· 菲涅耳假设，在9=o的方向上，倾斜因子x(©)有最大值， 而随着e的增大，x(e)迅速减小，在op与波阵面相切时， 6=，)为零。所有与波阵面相切的点，在波阵面上 构成一条轨迹。·

  K ds r e r Ae E P ikr ikr    Σ  0 0 ~