
引用1.4: 对于多次散射,我们假设位于τ处、传播方向为2的辐 射强度为1(:,2),则它散射到方向2的辐射强度为: I(t,D2') P(2,2') 4元 则多次散射产生的源函数为来自所有方向、并经散射, 到方向①的辐射总和。即上式对方向Ω在4π空间的积 分,即: ∫1(x,2')a P(2,2') 2 4π
则多次散射产生的源函数为来自所有方向、并经散射, 到方向Ω的辐射总和。即上式对方向Ω’在4π空间的积 分,即: 4 ' 4 ( , ') ( , ') d P I 对于多次散射,我们假设位于τ处、传播方向为Ω’的辐 射强度为I (τ, Ω’),则它散射到方向Ω的辐射强度为: 4 P( , ') I( , ') 引用1.4:
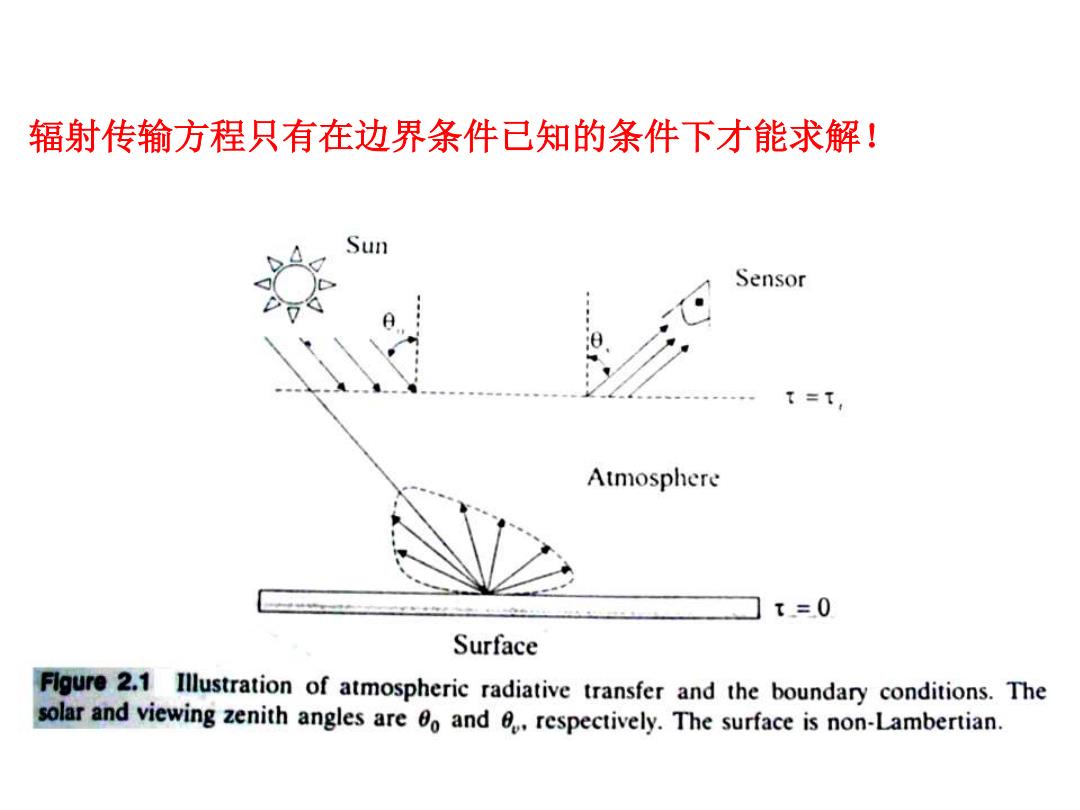
辐射传输方程只有在边界条件已知的条件下才能求解! Sun Sensor tT, Atmosphere t=0 Surface Flgure 2.1 Illustration of atmospheric radiative transfer and the boundary conditions.The solar and viewing zenith angles are 0 and respectively.The surface is non-Lambertian
辐射传输方程只有在边界条件已知的条件下才能求解!

大气顶层的上边界条件 I(x,-u,p)=δ(h-h)δ(p-po)πEs 地表处的下边界条件 0,40)=,公,o) I(u,o )u du do
I( t ,,) ( 0 )( 0 )E s 地表处的下边界条件 2 0 0 1 ( , , ' , ') 1 I(0, , ) R I( ' , ') 'd 'd ' 大气顶层的上边界条件

2.3大气辐射传输方程求解原理 2.3.1辐射场分解 (Radiation Field Decomposition) 2.3.2数值解法 ◆逐级散射法(Method of Successive Orders of Scattering) ◆离散坐标法(Method of Discrete Ordinates) 2.3.3近似解法
2.3 大气辐射传输方程求解原理 2.3.1 辐射场分解(Radiation Field Decomposition) 2.3.2 数值解法 逐级散射法(Method of Successive Orders of Scattering) 离散坐标法(Method of Discrete Ordinates) 2.3.3 近似解法

2.3.1辐射场分解 I=+ 下行辐射的直射部分: T(t,-山,p)=E,δ(u-h)δ(p-p) exp(-- Lo 漫辐射亮度ID dIp(t,u,p) L In(t,u,p)- dt ,1(z,4,p,)P(h,p,4,p,)du,o P(山,p,-ho,P)E,e-x/g 4
exp( ) ( , , ) ( ) ( ) 0 0 0 t I E s I I I I D 下行辐射的直射部分: 漫辐射亮度 I D / 0 0 0 2 0 1 1 ( , , , ) 4 ( , , ) ( , , , ) 4 ( , , ) ( , , ) t P E e I P d d I d dI s D i i i i i i D D 2.3.1 辐射场分解