
RB-INSERT(T,) 1 y =T.nil RB-Insert(T,z) 2 x =T.root 3 whilex≠T.nil 4 y=x 。关注: 5 if z.key <x.key ·16行:强制置新节点为红色 6 x =x.left 7 else x =x.right ·17行:重新着色,维持红黑特性 8 z.p=y ·只要维持了红黑特性,平衡性就能 9 if y =T.nil 得以保障 10 T.root 11 elseif z.key y.key 12 y.left=z 13 else y.right 14 z.left T.nil 15 z.right T.nil 16 .color RED 17 RB-INSERT-FIXUP(T
RB-Insert(T,z) • 关注: • 16行:强制置新节点为红色 • 17行:重新着色,维持红黑特性 • 只要维持了红黑特性,平衡性就能 得以保障

如何去fixup? ·冲突是由z引起的:z和z的父亲都是红色 ·不能简单地修改其中一个元素的颜色为黑色! ·黑高的定义就不well define了 ·在尽可能近的祖先为根的子树中,进行红黑颜色的互换! ·其中,可能会涉及旋转。 ·可能会出现冲突沿路径上移 ·Z为根的子树中,不会有冲突! ·分情形证明法十分关键: ·各种冲突类型,分别有效应对
如何去fixup? • 冲突是由z引起的:z和z的父亲都是红色 • 不能简单地修改其中一个元素的颜色为黑色! • 黑高的定义就不well define了 • 在尽可能近的祖先为根的子树中,进行红黑颜色的互换! • 其中,可能会涉及旋转。 • 可能会出现冲突沿路径上移 • Z为根的子树中,不会有冲突! • 分情形证明法十分关键: • 各种冲突类型,分别有效应对
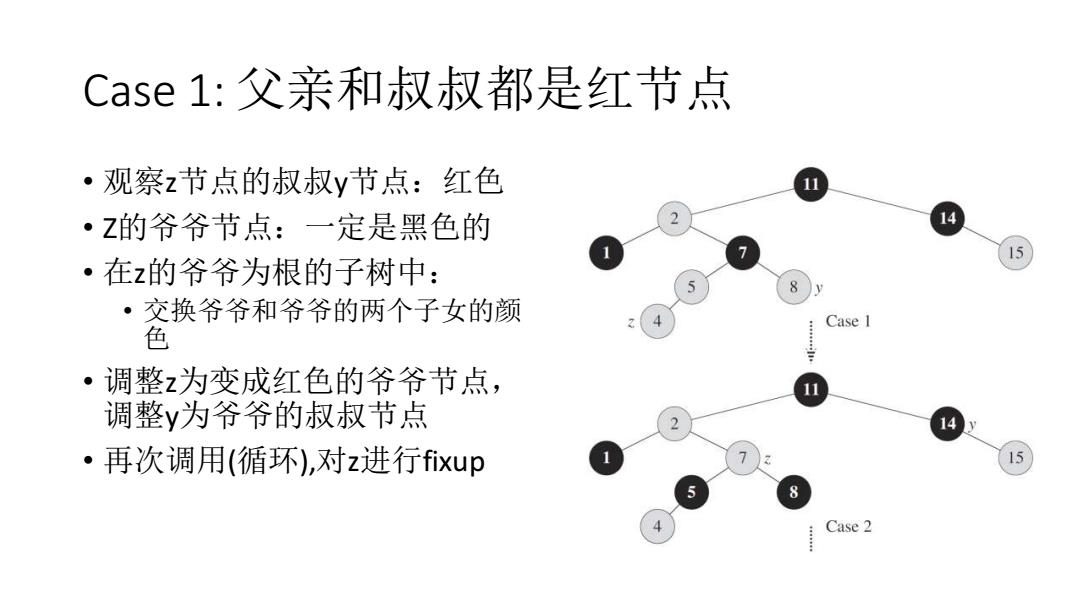
Case1:父亲和叔叔都是红节点 ·观察z节点的叔叔y节点:红色 ·Z的爷爷节点:一定是黑色的 4 ·在z的爷爷为根的子树中: ·交换爷爷和爷爷的两个子女的颜 Case 1 色 ·调整z为变成红色的爷爷节点, 调整y为爷爷的叔叔节点 ·再次调用(循环),对z进行fixup Case 2
Case 1: 父亲和叔叔都是红节点 • 观察z节点的叔叔y节点:红色 • Z的爷爷节点:一定是黑色的 • 在z的爷爷为根的子树中: • 交换爷爷和爷爷的两个子女的颜 色 • 调整z为变成红色的爷爷节点, 调整y为爷爷的叔叔节点 • 再次调用(循环),对z进行fixup