
Lemma 13.1 A red-black tree with n internal nodes has height at most 21g(n+1). ●Proof:. We start by showing that the subtree rooted at any node x contains at least 2bh(x)-1 internal nodes. If x is the root,the tree contains at least 2bh(root)-1 internal nodes ·n≥2 bh(root))-1 Let h be the height of the tree.The black-height of the root must be at least h/2;thus,n22h/2-1
• Proof: • We start by showing that the subtree rooted at any node x contains at least 2bh(x) -1 internal nodes. • If x is the root, the tree contains at least 2bh(root) -1 internal nodes • n≥ 2 bh(root) -1 • Let h be the height of the tree. The black-height of the root must be at least h/2; thus, n≥2 h/2 -1

Subtree rooted at any node x contains at least 2bh(x)-1 internal nodes Proof (induction on the height of x): ·Base: If the height of x is 0,then x must be a leaf(T.nil),and the subtree rooted at x indeed contains at least 20-1=0 internal nodes 。Induction: Suppose x has positive height and is an internal node with two children. Each child has a black-height of either bh(x)or bh(x)-1,depending on whether its color is red or black Since the height of a child of x is less than the height of x itself,we can apply the inductive hypothesis to conclude that each child has at least 2bh(x)-1-1 internal nodes. Thus,the subtree rooted at x contains at least(2bh(x)-1-1)+(2bh(x)-1-1)+1=2bh(x)-1 internal nodes
• Proof (induction on the height of x): • Base: • If the height of x is 0, then x must be a leaf (T.nil), and the subtree rooted at x indeed contains at least 20 -1 = 0 internal nodes • Induction: • Suppose x has positive height and is an internal node with two children. • Each child has a black-height of either bh(x) or bh(x)-1, depending on whether its color is red or black • Since the height of a child of x is less than the height of x itself, we can apply the inductive hypothesis to conclude that each child has at least 2bh(x)-1 -1 internal nodes. • Thus, the subtree rooted at x contains at least (2bh(x)-1 -1)+ (2bh(x)-1 -1)+1=2bh(x) -1 internal nodes Subtree rooted at any node x contains at least 2bh(x) -1 internal nodes
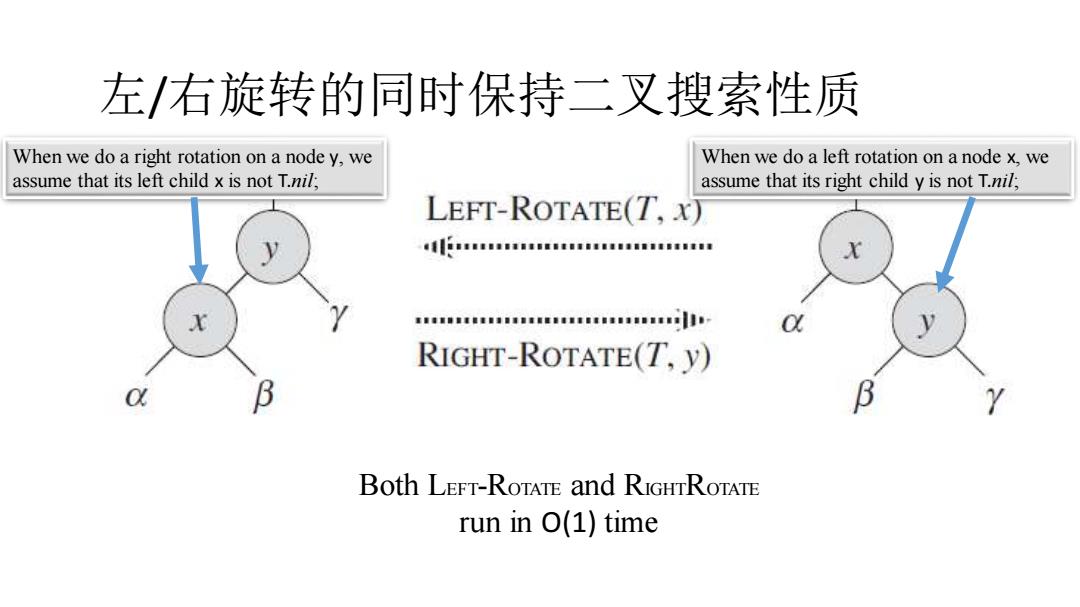
左/右旋转的同时保持二叉搜索性质 When we do a right rotation on a node y,we When we do a left rotation on a node x,we assume that its left child x is not T.nil; assume that its right child y is not T.nil; LEFT-ROTATE(T.x) RIGHT-ROTATE(T,y) Both Left-RoTATE and RightRoTATe run in O(1)time
左/右旋转的同时保持二叉搜索性质 When we do a left rotation on a node x, we assume that its right child y is not T.nil; Both LEFT-ROTATE and RIGHTROTATE run in O(1) time When we do a right rotation on a node y, we assume that its left child x is not T.nil;
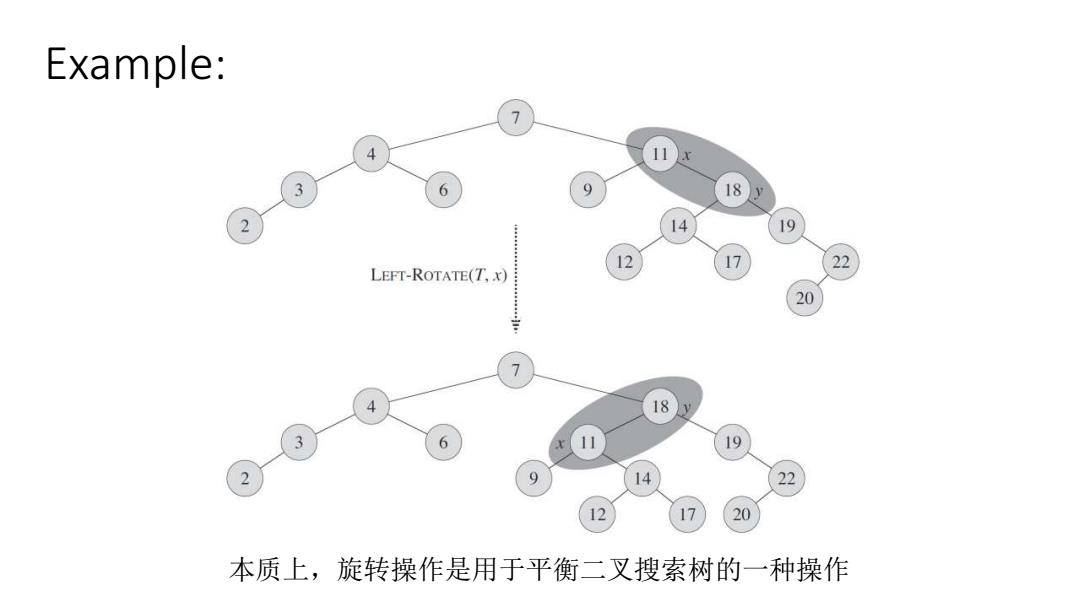
Example: 7 11 6 9 18y 14 19 12 22 LEFT-ROTATE(T,x) 20 18 6 19 9 4 本质上,旋转操作是用于平衡二叉搜索树的一种操作
Example: 本质上,旋转操作是用于平衡二叉搜索树的一种操作

红黑树的插入操作 ·采用BST的插入算法进行插入。插入元素的color被置为red。 ·这样的插入操作会破坏红黑树的特征吗? ·会! ·如果是插入的是根节点,破坏第二条 ·根是黑节点 ·如果插入的是叶节点,但是其父亲是red节点,破坏第四条 ·第四条:红色节点的子女必须是黑节点 其它几条会破 坏吗?
红黑树的插入操作 • 采用BST的插入算法进行插入。插入元素的color被置为red。 • 这样的插入操作会破坏红黑树的特征吗? • 会! • 如果是插入的是根节点,破坏第二条 • 根是黑节点 • 如果插入的是叶节点,但是其父亲是red节点,破坏第四条 • 第四条:红色节点的子女必须是黑节点 其它几条会破 坏吗?