4数据类型及其转换 4.1数据类型 在本文本中,数据类型包括比特串、字节串、域元素、椭圆曲线上的点和整数。 比特串:有序的0和1的序列。 字节串:有序的字节序列,其中8比特为1个字节。 域元素:有限域F,中的元素。 椭圆曲线上的点:椭圆曲线上的点P∈E(Fa),或者是一对域元素xp,yp),其中域元素xp和yp满足 椭圆曲线方程,或者是无穷远点O。 点的字节串表示有多种形式,用一个字节PC加以标识。无穷远点O的字节串表示是单一的零字 节PC=00。非无穷远点P=(xP,yp)有如下三种字节串表示形式: a)压缩表示形式,PC=02或03: b)未压缩表示形式,PC=04: c)混合表示形式,PC=06或07。 注:混合表示形式既包含压缩表示形式又包含未压缩表示形式。在实现中,它允许转换到压缩表示形式或者未压 缩表示形式。 对于椭圆曲线上点的压缩表示形式和混合表示形式,本文本中定为可选形式。椭圆曲线上点的压 缩表示形式参见附录A.5。 4.2数据类型转换 图1提供了各种数据类型之间的转换关系,线上的标志是相应数据转换方法所在的条。 4.2.7条 域元素 4.2.5条 4.2.6条 4.2.4条 4.2.1条 比特串 字节串 整数 4.2.3条 4.2.2条 4.2.9条 4.2.8条 点 图1数据类型和转换约定 4.2.1整数到字节串的转换 输入:非负整数x,以及字节串的目标长度k(其中k满足2歇>x)。 输出:长度为k的字节串M。 a)设Mk-1,Mk-2,·,Mo是M的从最左边到最右边的字节: b)M的字节满足:
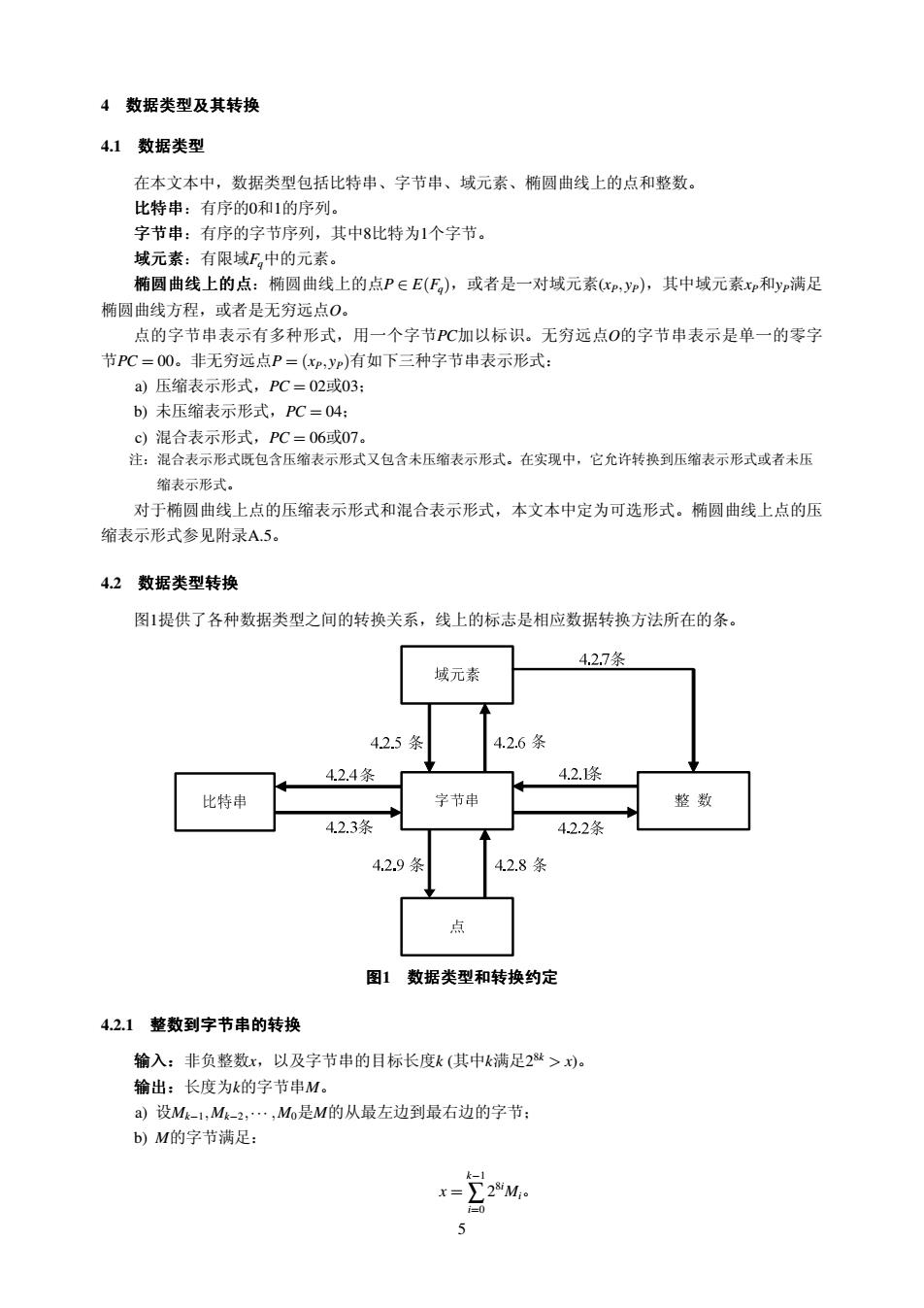
4 数据类型及其转换 4.1 数据类型 在本文本中,数据类型包括比特串、字节串、域元素、椭圆曲线上的点和整数。 比特串:有序的0和1的序列。 字节串:有序的字节序列,其中8比特为1个字节。 域元素:有限域Fq中的元素。 椭圆曲线上的点:椭圆曲线上的点P ∈ E(Fq),或者是一对域元素(xP,yP),其中域元素xP和yP满足 椭圆曲线方程,或者是无穷远点O。 点的字节串表示有多种形式,用一个字节PC加以标识。无穷远点O的字节串表示是单一的零字 节PC = 00。非无穷远点P = (xP,yP)有如下三种字节串表示形式: a) 压缩表示形式,PC = 02或03; b) 未压缩表示形式,PC = 04; c) 混合表示形式,PC = 06或07。 注:混合表示形式既包含压缩表示形式又包含未压缩表示形式。在实现中,它允许转换到压缩表示形式或者未压 缩表示形式。 对于椭圆曲线上点的压缩表示形式和混合表示形式,本文本中定为可选形式。椭圆曲线上点的压 缩表示形式参见附录A.5。 4.2 数据类型转换 图1提供了各种数据类型之间的转换关系,线上的标志是相应数据转换方法所在的条。 图1 数据类型和转换约定 4.2.1 整数到字节串的转换 输入:非负整数x,以及字节串的目标长度k (其中k满足2 8k > x)。 输出:长度为k的字节串M。 a) 设Mk−1,Mk−2,··· ,M0是M的从最左边到最右边的字节; b) M的字节满足: x = k−1 ∑ i=0 2 8iMi。 5

4.2.2字节串到整数的转换 输入:长度为k的字节串M。 输出:整数x。 a)设Mk-1,Mk-2,…,Mo是M的从最左边到最右边的字节; b)将M转换为整数x: 4.2.3比特串到字节串的转换 输入:长度为m的比特串s。 输出:长度为k的字节串M,其中k=「m/8]。 a)设sm-1,Sm-2,…,So是s从最左边到最右边的比特: b)设Mk-1,M-2,·,Mo是M从最左边到最右边的字节,则 M=s8+758i+6…58+1sS8,其中0≤i<k,当8i+j≥m,0<j≤7时,sS8i+j=0。 4.2.4字节串到比特串的转换 输入:长度为k的字节串M。 输出:长度为m的比特串s,其中m=8k。 a)设Mk-1,Mk-2,·,Mo是M从最左边到最右边的字节; b)设sm-1,Sm-2,·,s0是s从最左边到最右边的比特,则s是M右起第i-8j+1比特,其中j=/8。 4.2.5域元素到字节串的转换 输入:F,中的元素a。 输出:长度1=[t/8]的字节串S,其中1=1og2ql。 )若q为奇素数,则a必为区间[0,9-1]中的整数,按4.2.1的细节把oa转换成长度为l的字节串S: b)若q=2m,则o必为长度为m的比特串,按4.2.3的细节把a转换成长度为1的字节串S; 4.2.6字节串到域元素的转换 输入:基域F的类型,长度为1=[t/8]的字节串S,其中1=og2q小。 输出:F,中的元素。 a)若q是奇素数,则按4.2.2的细节将S转换为整数a,若a生[0,q-1,则报错: b)若q=2m,则按4.2.4的细节将S转换为长度为m的比特串0。 4.2.7域元素到整数的转换 输入:域F,中的元素。 输出:整数x。 a)若g为奇素数,则r=(不需要转换) b)若g=2m,则α必为长度为m的比特串,设sm-1,Sm-2,·,so是0的从最左边到最右边的比特, 将o转化为整数x: X= 6
4.2.2 字节串到整数的转换 输入:长度为k的字节串M。 输出:整数x。 a) 设Mk−1,Mk−2,··· ,M0是M的从最左边到最右边的字节; b) 将M转换为整数x: x = k−1 ∑ i=0 2 8iMi。 4.2.3 比特串到字节串的转换 输入:长度为m的比特串s。 输出:长度为k的字节串M,其中k = ⌈m/8⌉。 a) 设sm−1,sm−2,··· ,s0是s从最左边到最右边的比特; b) 设Mk−1,Mk−2,··· ,M0是M从最左边到最右边的字节,则 Mi = s8i+7s8i+6 ···s8i+1s8i,其中0 ≤ i < k,当8i+ j ≥ m,0 < j ≤ 7时,s8i+j = 0。 4.2.4 字节串到比特串的转换 输入:长度为k的字节串M。 输出:长度为m的比特串s,其中m = 8k。 a) 设Mk−1,Mk−2,··· ,M0是M从最左边到最右边的字节; b) 设sm−1,sm−2,··· ,s0是s从最左边到最右边的比特,则si是Mj右起第i-8 j+1比特,其中j = ⌊i/8⌋。 4.2.5 域元素到字节串的转换 输入:Fq中的元素α。 输出:长度l = ⌈t/8⌉的字节串S,其中t = ⌈log2 q⌉。 a) 若q为奇素数,则α必为区间[0,q−1]中的整数,按4.2.1的细节把α转换成长度为l的字节串S; b) 若q = 2 m,则α必为长度为m的比特串,按4.2.3的细节把α转换成长度为l的字节串S; 4.2.6 字节串到域元素的转换 输入:基域Fq的类型,长度为l = ⌈t/8⌉的字节串S,其中t = ⌈log2 q⌉。 输出:Fq中的元素α。 a) 若q是奇素数,则按4.2.2的细节将S转换为整数α,若α ∈/ [0,q−1],则报错; b) 若q = 2 m,则按4.2.4的细节将S转换为长度为m的比特串α。 4.2.7 域元素到整数的转换 输入:域Fq中的元素α。 输出:整数x。 a) 若q为奇素数,则x = α (不需要转换); b) 若q = 2 m,则α必为长度为m的比特串,设sm−1,sm−2,··· ,s0是α的从最左边到最右边的比特, 将α转化为整数x: x = m−1 ∑ i=0 2 i si。 6

4.2.8点到字节串的转换 输入:椭圆曲线上的点P=(xP,yP),且P≠O。 输出:字节串S。若选用未压缩表示形式或混合表示形式,则输出字节串长度为2!+1:若选用压 缩表示形式,则输出字节串长度为l+1.1=(1og2q)/81。) a)按4.2.5中的细节把域元素xp转换成长度为l的字节串X1: b)若选用压缩表示形式,则: b.1)计算比特p:(参见附录A.5。) b.2)若p=0,则令PC=02:若p=1,则令PC=03: b.3)字节串S=PC‖X1: c)若选用未压缩表示形式,则: c.1)按4.2.5的细节把域元素yp转换成长度为l的字节串Y: c.2)令PC=04: c.3)字节串S=PC‖X1‖Y: d若选用混合表示形式,则: d.1)按4.2.5的细节把域元素yp转换成长度为的字节串Y1: d.2)计算比特p:(参见附录A.5。) d.3)若p=0,则令PC=06:若p=1,则令PC=07: d.4)字节串S=PC‖X‖Y1。 4.2.9字节串到点的转换 输入:定义F,上椭圆曲线的域元素a、b,字节串S。若选用未压缩表示形式或混合表示形式,则 字节串S长度为21+1:若选用压缩表示形式,则字节串S长度为1+1。(1=「(1og2q)/81。) 输出:椭圆曲线上的点P=(cP,yp),且P≠O。 )若选用压缩表示形式,则S=PC‖X1:若选用未压缩表示形式或混合表示形式,则S=PC‖ X‖Y,其中PC是单一字节,X和Y都是长度为的字节串: b)按4.2.6的细节把字节串X1转换成域元素xp: c)若选用压缩表示形式,则: c.1)检验PC=02或者是PC=03,若不是这种情形,则报错: c.2)若PC=02,则令p=0:若PC=03,则令p=1: c.3)将(p,p)转换为椭圆曲线上的一个点(cp,yp):(参见附录A.5。) d)若选用未压缩表示形式,则: d.1)检验PC=04,若不是这种情形,则报错: d.2)按4.2.6的细节把字节串Y1转换成域元素yp: e)若选用混合表示形式,则: e.1)检验PC=06或者PC=07,若不是这种情形,则报错: e.2)执行步骤e.2.1)或者e.2.2): e.2.1)按4.2.6的细节把字节串Y转换成域元素yp; e.2.2)若PC=06,则令yp=0,否则令p=1;将(xp,p)转换为椭圆曲线上的一个点(xp,yp): (参见附录A.5。) )若q为奇素数,则验证y三x+axp十b(modq),若不是这种情形,则报错: 若q=2m,则在F中验证y+xpyp=x+a子+b,若不是这种情形,则报错: g)P=(xp,yp)
4.2.8 点到字节串的转换 输入:椭圆曲线上的点P = (xP,yP),且P ̸= O。 输出:字节串S。若选用未压缩表示形式或混合表示形式,则输出字节串长度为2l +1;若选用压 缩表示形式,则输出字节串长度为l+1。(l = ⌈(log2 q)/8⌉。) a) 按4.2.5中的细节把域元素xP转换成长度为l的字节串X1; b) 若选用压缩表示形式,则: b.1) 计算比特y˜P;(参见附录A.5。) b.2) 若y˜P = 0,则令PC = 02;若y˜P = 1,则令PC = 03; b.3) 字节串S = PC ∥ X1; c) 若选用未压缩表示形式,则: c.1) 按4.2.5的细节把域元素yP转换成长度为l的字节串Y1; c.2) 令PC = 04; c.3) 字节串S = PC ∥ X1 ∥ Y1; d) 若选用混合表示形式,则: d.1) 按4.2.5的细节把域元素yP转换成长度为l的字节串Y1; d.2) 计算比特y˜P;(参见附录A.5。) d.3) 若y˜P = 0,则令PC = 06;若y˜P = 1,则令PC = 07; d.4) 字节串S = PC ∥ X1 ∥ Y1。 4.2.9 字节串到点的转换 输入:定义Fq上椭圆曲线的域元素a、b,字节串S。若选用未压缩表示形式或混合表示形式,则 字节串S长度为2l +1;若选用压缩表示形式,则字节串S长度为l +1。( l = ⌈(log2 q)/8⌉。) 输出:椭圆曲线上的点P = (xP,yP),且P ̸= O。 a) 若选用压缩表示形式,则S = PC ∥ X1;若选用未压缩表示形式或混合表示形式,则S = PC ∥ X1 ∥ Y1,其中PC是单一字节,X1和Y1都是长度为l的字节串; b) 按4.2.6的细节把字节串X1转换成域元素xP; c) 若选用压缩表示形式,则: c.1) 检验PC = 02或者是PC = 03,若不是这种情形,则报错; c.2) 若PC = 02,则令y˜P = 0;若PC = 03,则令y˜P = 1; c.3) 将(xP,y˜P)转换为椭圆曲线上的一个点(xP,yP);(参见附录A.5。) d) 若选用未压缩表示形式,则: d.1) 检验PC = 04,若不是这种情形,则报错; d.2) 按4.2.6的细节把字节串Y1转换成域元素yP; e) 若选用混合表示形式,则: e.1) 检验PC = 06或者PC = 07,若不是这种情形,则报错; e.2) 执行步骤e.2.1)或者e.2.2): e.2.1) 按4.2.6的细节把字节串Y1转换成域元素yP; e.2.2) 若PC = 06,则令y˜P = 0,否则令y˜P = 1;将(xP,y˜P)转换为椭圆曲线上的一个点(xP,yP); (参见附录A.5。) f) 若q为奇素数,则验证y 2 P ≡ x 3 P +axP +b (modq),若不是这种情形,则报错; 若q = 2 m,则在F2 m中验证y 2 P +xPyP = x 3 P +ax2 P +b,若不是这种情形,则报错; g) P = (xP,yP)。 7

5椭圆曲线系统参数及其验证 5.1一般要求 椭圆曲线系统参数是可以公开的,系统的安全性不依赖于对这些参数的保密。本文本不规定椭圆 曲线系统参数的生成方法,但规定了系统参数的验证方法。椭圆曲线阶的计算和基点的选取方法可参 见附录B.3,曲线参数的生成方法可参见附录D。 椭圆曲线系统参数按照基域的不同可以分为两种情形: 一当基域是F(p为大于3的素数)时,F。上的椭圆曲线系统参数: 一当基域是F时,F上的椭圆曲线系统参数。 5.2F,上椭圆曲线系统参数及其验证 5.2.1Fn上椭圆曲线系统参数 F。上椭圆曲线系统参数包括: a)域的规模g=p,p是大于3的素数: b)(选项)一个长度至少为192的比特串SEED(若按照附录D描述的方法产生椭圆曲线): c)F,中的两个元素a和b,它们定义椭圆曲线E的方程:y2=x3+ax+b: d)基点G=(xG,yG)∈E(F),G≠O: e)基点G的阶n(要求:n>2I91且n>4p/2): )(选项)余因子h=#E(Fp)/n。 5.2.2Fn上椭圆曲线系统参数的验证 下面的条件应由椭圆曲线系统参数的生成者加以验证。椭圆曲线系统参数的用户可选择验证这些 条件。 输入:F。上椭圆曲线系统参数的集合。 输出:若椭圆曲线系统参数是有效的,则输出“有效”:否则输出“无效”。 a)验证q=p是奇素数:(参见附录B.1.10。) b)验证a、b、xc和yc是区间[0,p-1中的整数: c)若按照附录D描述的方法拟随机产生椭圆曲线,验证SEED是长度至少为192的比特串,且a, b由SEED派生得到: d)验证(4a3+27b2)modp≠0: e)验证y2≡x2十axc+b(modp): f)验证n是素数,n>2191且n>4p/P:(参见附录B.l.10。) g)验证[nG=O:(参见附录A.3。) h)(选项)计算H=(p/2+1)2/n,并验证h=H: )验证抗MOV攻击条件和抗异常曲线攻击条件成立:(参见附录A.4.2.1和A.4.2.2。) )若以上任何一个验证失败,则输出“无效”:否则,输出“有效”。 53F上椭圆曲线系统参数及其验证 5.3.1F,m上椭圆曲线系统参数 F2上的椭圆曲线系统参数包括: a)域的规模q=2m,对Fm中元素表示法(三项式基TPB、五项式基PPB或高斯正规基GNB)的标识, 一个F2上的m次约化多项式(若所用的基是TPB或PPB): 8
5 椭圆曲线系统参数及其验证 5.1 一般要求 椭圆曲线系统参数是可以公开的,系统的安全性不依赖于对这些参数的保密。本文本不规定椭圆 曲线系统参数的生成方法,但规定了系统参数的验证方法。椭圆曲线阶的计算和基点的选取方法可参 见附录B.3,曲线参数的生成方法可参见附录D。 椭圆曲线系统参数按照基域的不同可以分为两种情形: ――当基域是Fp(p为大于3的素数)时,Fp上的椭圆曲线系统参数; ――当基域是F2 m时,F2 m上的椭圆曲线系统参数。 5.2 Fp上椭圆曲线系统参数及其验证 5.2.1 Fp上椭圆曲线系统参数 Fp上椭圆曲线系统参数包括: a) 域的规模q = p,p是大于3的素数; b) (选项)一个长度至少为192的比特串SEED(若按照附录D描述的方法产生椭圆曲线); c) Fp中的两个元素a和b,它们定义椭圆曲线E的方程:y 2 = x 3 +ax+b; d) 基点G = (xG,yG) ∈ E(Fp),G ̸= O; e) 基点G的阶n(要求:n > 2 191且n > 4p 1/2 ); f) (选项)余因子h = #E(Fp)/n。 5.2.2 Fp上椭圆曲线系统参数的验证 下面的条件应由椭圆曲线系统参数的生成者加以验证。椭圆曲线系统参数的用户可选择验证这些 条件。 输入:Fp上椭圆曲线系统参数的集合。 输出:若椭圆曲线系统参数是有效的,则输出“有效”;否则输出“无效”。 a) 验证q = p是奇素数;(参见附录B.1.10。) b) 验证a、b、xG和yG是区间[0, p−1]中的整数; c) 若按照附录D描述的方法拟随机产生椭圆曲线,验证SEED是长度至少为192的比特串,且a, b由SEED派生得到; d) 验证(4a 3 +27b 2 ) modp ̸= 0; e) 验证y 2 G ≡ x 3 G +axG +b (modp); f) 验证n是素数,n > 2 191且n > 4p 1/2 ;(参见附录B.1.10。) g) 验证[n]G = O;(参见附录A.3。) h) (选项)计算h ′ = ⌊ (p 1/2 +1) 2/n ⌋ ,并验证h = h ′; i) 验证抗MOV攻击条件和抗异常曲线攻击条件成立;(参见附录A.4.2.1和A.4.2.2。) j) 若以上任何一个验证失败,则输出“无效”;否则,输出“有效”。 5.3 F2 m上椭圆曲线系统参数及其验证 5.3.1 F2 m上椭圆曲线系统参数 F2 m上的椭圆曲线系统参数包括: a) 域的规模q = 2 m,对F2 m中元素表示法(三项式基TPB、五项式基PPB或高斯正规基GNB)的标识, 一个F2上的m次约化多项式(若所用的基是TPB或PPB); 8

b)(选项)一个长度至少为192的比特串SEED(若按照附录D描述的方法拟随机产生椭圆曲线): c)F中的两个元素a和b,它们定义椭圆曲线E的方程:y2+xy=x3+ax2+b: d)基点G=(xG,yG)∈E(F-),G卡O: e)基点G的阶n(要求:n>2191且n>22+m/2): D(选项)余因子h=#E(F)/n。 53.2F2m上椭圆曲线系统参数的验证 下面的条件应由椭圆曲线系统参数的生成者加以验证。椭圆曲线系统参数的用户可选择验证这些 条件。 输入:F2m上椭圆曲线系统参数的集合。 输出:若椭圆曲线系统参数是有效的,则输出“有效”:否则输出“无效”。 )对某个m,验证q=2m:若所用的是TPB,则验证约化多项式是F上的不可约三项式(参见 表A.3):若所用的是PPB,则验证不存在m次不可约三项式,且约化多项式是F上的不可约五 项式(参见表A.4):若所用的是GNB,则验证m不能被8整除: b)验证a,b,xc和yc是长度为m的比特串: c)若按照附录D描述的方法拟随机产生椭圆曲线,验证SEED是长度至少为192的比特串,且a, b由SEED派生得到: d)验证b卡0: e)在Fm中验证y2+xcyG=x2+ar记+b: f)验证n是一个素数,n>2191且n>22+m/2:(参见附录B.1.10。) g)验证[nG=O:(参见附录A.3.2。) h)(选项)计算H=(2m2+1)2/n,验证h=t; i)验证抗MOV攻击条件成立:(参见附录A.4.2.1。) )若以上任何一个验证失败,则输出“无效”:否则输出“有效”。 6密钥对的生成与公钥的验证 6.1密钥对的生成 输入:一个有效的F,(q=p且p为大于3的素数,或q=2m)上椭圆曲线系统参数的集合。 输出:与椭圆曲线系统参数相关的一个密钥对(d,P)。 a)用随机数发生器产生整数d∈[1,n-2]: b)G为基点,计算点P=(xP,yp)=[dG:(参见附录A.3.2。) c)密钥对是(d,P),其中d为私钥,P为公钥。 6.2公钥的验证 6.21Fn上椭圆曲线公钥的验证 输入:一个有效的F(p>3且p为素数)上椭圆曲线系统参数集合及一个相关的公钥P。 输出:对于给定的椭圆曲线系统参数,若公钥P是有效的,则输出“有效”;否则输出“无效”。 a)验证P不是无穷远点O: b)验证公钥P的坐标xp和yp是域F,中的元素:(即验证xp和yp是区间[O,p-中的整数。) c)验证y2≡x2+axp+b(modp) d)验证[nlP=O: )若通过了所有验证,则输出“有效”:否则输出“无效
b) (选项) 一个长度至少为192的比特串SEED(若按照附录D描述的方法拟随机产生椭圆曲线); c) F2 m中的两个元素a和b,它们定义椭圆曲线E的方程:y 2 +xy = x 3 +ax2 +b; d) 基点G = (xG,yG) ∈ E(F2 m ),G ̸= O; e) 基点G的阶n(要求:n > 2 191且n > 2 2+m/2 ); f) (选项)余因子h = #E(F2 m )/n。 5.3.2 F2 m上椭圆曲线系统参数的验证 下面的条件应由椭圆曲线系统参数的生成者加以验证。椭圆曲线系统参数的用户可选择验证这些 条件。 输入:F2 m上椭圆曲线系统参数的集合。 输出:若椭圆曲线系统参数是有效的,则输出“有效”;否则输出“无效”。 a) 对某个m,验证q = 2 m;若所用的是TPB,则验证约化多项式是F2上的不可约三项式(参见 表A.3);若所用的是PPB,则验证不存在m次不可约三项式,且约化多项式是F2上的不可约五 项式(参见表A.4);若所用的是GNB,则验证m不能被8整除; b) 验证a,b,xG和yG是长度为m的比特串; c) 若按照附录D描述的方法拟随机产生椭圆曲线,验证SEED是长度至少为192的比特串,且a, b由SEED派生得到; d) 验证b ̸= 0; e) 在F2 m中验证y 2 G +xGyG = x 3 G +ax2 G +b; f) 验证n是一个素数,n > 2 191且n > 2 2+m/2 ;(参见附录B.1.10。) g) 验证[n]G = O;(参见附录A.3.2。) h) (选项)计算h ′ = ⌊ (2 m/2 +1) 2/n ⌋ ,验证h = h ′; i) 验证抗MOV攻击条件成立;(参见附录A.4.2.1。) j) 若以上任何一个验证失败,则输出“无效”;否则输出“有效”。 6 密钥对的生成与公钥的验证 6.1 密钥对的生成 输入:一个有效的Fq(q = p且p为大于3的素数,或q = 2 m )上椭圆曲线系统参数的集合。 输出:与椭圆曲线系统参数相关的一个密钥对(d,P)。 a) 用随机数发生器产生整数d ∈ [1,n−2]; b) G为基点,计算点P = (xP,yP) = [d]G;(参见附录A.3.2。) c) 密钥对是(d,P),其中d为私钥,P为公钥。 6.2 公钥的验证 6.2.1 Fp上椭圆曲线公钥的验证 输入:一个有效的Fp(p > 3且p为素数)上椭圆曲线系统参数集合及一个相关的公钥P。 输出:对于给定的椭圆曲线系统参数,若公钥P是有效的,则输出“有效”;否则输出“无效”。 a) 验证P不是无穷远点O; b) 验证公钥P的坐标xP和yP是域Fp中的元素;(即验证xP和yP是区间[0, p−1]中的整数。) c) 验证y 2 P ≡ x 3 P +axP +b (modp); d) 验证[n]P = O; e) 若通过了所有验证,则输出“有效”;否则输出“无效”。 9