
◆不 15 第二部分公钥密码和散列函数 第8章:数论入门 第9章:公钥密码与RSA 第10章:密钥管理和其他公钥密码体制 第11章:消息认证和散列函数 第12章:散列和MAC算法 第13章:数字签名和认证协议 评 2022/10/9 现代密码学理论与实践-08 2/70
2022/10/9 现代密码学理论与实践-08 2/70 第二部分 公钥密码和散列函数 第8章:数论入门 第9章:公钥密码与RSA 第10章:密钥管理和其他公钥密码体制 第11章:消息认证和散列函数 第12章:散列和MAC算法 第13章:数字签名和认证协议

Chapter 8 Introduction to Number Theory The Devil said to Daniel Webster:"Set me a task I can't carry out,and I'll give you anything in the world you ask for. Daniel Webster:"Fair enough.Prove that for n greater than 2, the equation an b ch has no non-trivial solution in the integers. They agreed on a three-day period for the labor,and the Devil disappeared. At the end of three days,the Devil presented himself,haggard, jumpy,biting his lip.Daniel Webster said to him,"Well,how did you do at my task?Did you prove the theorem?' "Eh?No...no,I haven't proved it." "Then I can have whatever I ask for?Money?The Presidency?' "What?Oh,that-of course.But listen!If we could just prove the following two lemmas-" -The Mathematical Magpie,Clifton Fadiman 2022/10/9 现代密码学理论与实践-08 3/70
2022/10/9 现代密码学理论与实践-08 3/70 Chapter 8 Introduction to Number Theory The Devil said to Daniel Webster: "Set me a task I can't carry out, and I'll give you anything in the world you ask for." Daniel Webster: "Fair enough. Prove that for n greater than 2, the equation an + bn = cn has no non-trivial solution in the integers." They agreed on a three-day period for the labor, and the Devil disappeared. At the end of three days, the Devil presented himself, haggard, jumpy, biting his lip. Daniel Webster said to him, "Well, how did you do at my task? Did you prove the theorem?' "Eh? No . . . no, I haven't proved it." "Then I can have whatever I ask for? Money? The Presidency?' "What? Oh, that—of course. But listen! If we could just prove the following two lemmas—" —The Mathematical Magpie, Clifton Fadiman

15 本章要点 素数是一种整数,在整除意义下,它只能被自身(正 负)和1整除。素数在数论和密码学里扮演重要角色。 ·在公钥密码中起重要作用的两个定理是费马定理和欧 拉定理 ● 许多密码算法的一个重要前提是能够选择一个大的素 数。开发有效算法判定一个随机整数是否为素数是密 码研究的重要课题 。 离散对数是许多公钥算法的基础。离散对数和普通对 数类似,但是在模算术上进行运算。 2022/10/9 现代密码学理论与实践-08 4170
2022/10/9 现代密码学理论与实践-08 4/70 本章要点 ⚫ 素数是一种整数,在整除意义下,它只能被自身(正 负)和1整除。素数在数论和密码学里扮演重要角色。 ⚫ 在公钥密码中起重要作用的两个定理是费马定理和欧 拉定理。 ⚫ 许多密码算法的一个重要前提是能够选择一个大的素 数。开发有效算法判定一个随机整数是否为素数是密 码研究的重要课题。 ⚫ 离散对数是许多公钥算法的基础。离散对数和普通对 数类似,但是在模算术上进行运算

包海作式不为 8.1素数Prime Numbers 15 ● 整数p>1是素数当且仅当它只有因子±1和±p,如 2,3,5,7是素数,而4,6,8,9,10不是素数 ●】 素数不能写作其他数的乘积形式 ·1是素数,但是通常没有什么用 ·素数是数论的核心 小于200的素数如下 235711131719232931374143 4753596167717379838997101 103107109113127131137139149151 157163167173179181191193197199 2022/10/9 现代密码学理论与实践-08 5/70
2022/10/9 现代密码学理论与实践-08 5/70 8.1 素数 Prime Numbers ⚫ 整数p>1是素数当且仅当它只有因子±1和±p,如 2,3,5,7是素数,而4,6,8,9,10不是素数 ⚫ 素数不能写作其他数的乘积形式 ⚫ 1是素数,但是通常没有什么用 ⚫ 素数是数论的核心 ⚫ 小于200的素数如下 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199
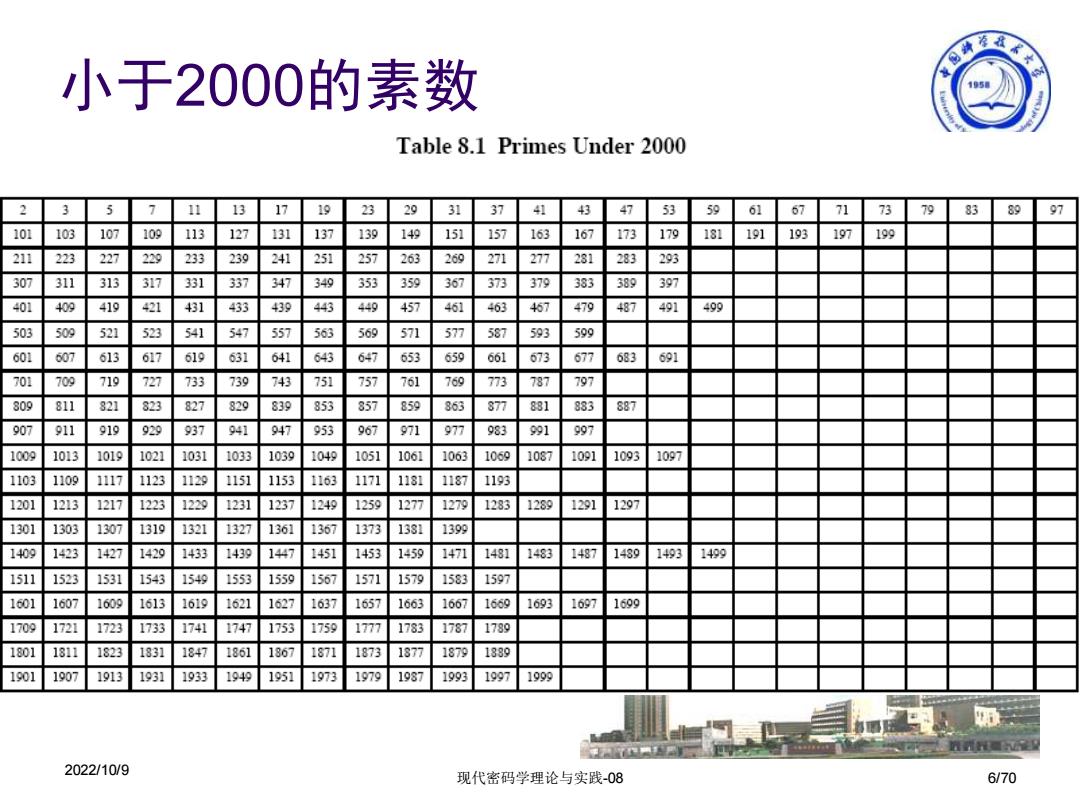
小于2000的素数 15 Table 8.1 Primes Under 2000 2 3 5 13 17 19 23 29 31 37 41 43 47 53 59 61 67 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229 233 239 241 251 257 263 269 271 277 231 283 293 307 311 313 317 331 337 347 349 353 359 367 373 379 383 389 397 401 409 419 421 431 433 439 443 449 457 461 463 467 479 487 491 499 503 509 521 523 541 547 557 563 569 571 577 587 593 599 601 607 613 617 619 631 641 643 647 653 659 661 673 677 683 691 701 709 719 727 733 739 743 751 757 761 769 773 787 797 809 811 821 823 827 829 839 853 857 859 863 877 831 833 887 907 911 919 929 937 941 947 953 967 971 977 983 991 997 1009 1013 1019 1021 1031 1033 1039 1049 1051 1061 1063 1069 1087 1091 1093 1097 1103 1109 1117 1123 1129 1151 1153 1163 1171 1181 1187 1193 1201 1213 1217 1223 1229 1231 1237 1249 1259 1277 1279 1283 1289 1291 1297 1301 1303 1307 1319 1321 1327 1361 1367 1373 1331 1399 1409 1423 1427 1429 1433 1439 1447 1451 1453 1459 1471 1481 1483 1487 1489 1493 1499 1511 1523 1531 1543 1549 1553 1559 1567 1571 1579 1583 1597 1601 1607 1609 1613 1619 1621 1627 1637 1657 1663 1667 1669 1693 1697 1699 1709 1721 1723 1733 1741 1747 1753 1759 1777 1783 1787 1789 1801 1311 1823 1831 1847 1861 1867 1871 1873 1877 1879 1389 1901 1907 1913 1931 1933 1949 1951 1973 1979 1987 1993 1997 1999 2022/10/9 现代密码学理论与实践-08 6/70
2022/10/9 现代密码学理论与实践-08 6/70 小于2000的素数